Science > Physics > Force > Simple Numerical Problems on Force
In this article, we shall study to solve numerical problems to calculate the magnitude of force, momentum, and change in momentum.
Example – 01:
The speed of a tortoise and hare are 1 m/s and 3 m/s respectively. The mass of the hare is 5 kg while that of tortoise is 20 kg. Which of the two has greater momentum?
Solution:
The momentum of hare = Mass of hare x Speed of hare= 5 x 3 = 15 kg m/s
The momentum of tortoise = Mass of tortoise x Speed of tortoise= 20 x 1 = 20 kg m/s
Thus the momentum of tortoise is more than that of the hare.
Example – 02:
What is the magnitude of force exerted by a horse in pulling a cart of mass 600 kg and accelerating at the rate of 1.2 m/s2?
Given: mass of cart = m = 600 kg, acceleration = a = 1.2 m/s2.
To Find: F =?
Solution:
By Newton’s second law of motion, magnitude of force
F = ma = 600 x 1.2
∴ F = 720 N
Ans: The required force is 720 N.
Example – 03:
An object of mass 10 kg is moving with the initial velocity of 10 m/s. A constant force acts on it for 4 s giving it a speed of 2 m/s in opposite direction. Find the acceleration and the force.
Given: mass of object = m = 10 kg, initial velocity = u = 10 m/s, Final velocity = v = – 2m/s (negative since it is in opposite direction), time for which force is acting = t = 4 s
To Find: acceleration = a =? Force acting = F =?
Solution:
a = (v – u)/t = (-2 – 10)/4 = -12/4 = -3 m/s2
The negative sign indicated retardation.
By newton’s second law of motion we have
F = ma = 10 x (-3) = -30 N
Negative sign indicated retarding force.
Ans: The acceleration = 3 m/s2 and Force = -30 N
Example – 04:
A constant force of 2 N acts on a body for 5 seconds to change its velocity. Calculate the change in the momentum.
Given: Force acting = F = 2 N, time for which the force is acting = t = 5s.
To Find: Change in momentum =?
Solution:
Change in momentum = F x t = 2 x 5 = 10 kg m/s.
Ans: the change in momentum is 10 kg m/s.
Example – 05:
An empty truck of mass 1000 kg is moving at a speed of 36 km/hr. It is loaded with 500 kg of material on its way and again moves at the same speed. Will the momentum of the truck remain the same after loading? if not, find the momentum of the truck after loading.
Given: Mass of a truck = 1000 kg, Mass of Load = 500 kg, Speed of the vehicle = v = 36 km/hr = 36 x 5/18 = 10 m/s.
To Find: Momentum of truck = p =?
Solution:
The momentum of a body depends on its mass. In this case, the truck is loaded on the way, hence its momentum should change.
Total Mass = m = 1000 + 500 = 1500 kg
New momentum = Total Mass x Velocity = 1500 X 10 = 15000 kg m/s
Ans: The momentum of the truck after loading is 15000 kg m/s.
Example – 06:
A railway wagon of mass 1000 kg is pulled with a force of 10000 N. What is the acceleration?
Given : Force applied = F = 10000 N, mass of wagon = m = 1000 kg.
To Find: acceleration = a =?,
Solution:
By Newton’s second law of motion, magnitude of force
F = ma
∴ 10000 = 1000 x a
∴ a = 10000/1000 = 10 m/s2.
Ans: The acceleration is 10 m/s2.
Example – 07:
A car of mass 1000 kg is moving at a certain speed when a constant braking force 1000 N acts on it for 5 s and speed of the car reduced to half the original speed. Find the further time required to stop the car, if the same constant force acts on it.
Given: mass of car = m = 1000 kg, Force acting = F = 1000 N,time taken = t = 5 s, Final speed (v) = 1/2 Initial speed (u) = u/2
To find: t =? when v = 0
Solution:
By Newton’s second law of motion, magnitude of force
F = ma
∴1000 = 1000 x a
∴ a = 1000/1000 = 1 m/s2.
By the first equation of motion
∴ a = (v – u)/t = (u/2 – u)/5 = (-u/2)/5 = (-u/10)
∴ a = -u/10 = – 1
∴ u = 10 m/s
We have v = u + at
∴ 0 = 10 + (-1)t
∴ -10 = – t
∴ t = 10 s
Ans: The further time required to stop the car is 10 s
Example – 08:
Find the magnitude of the force applied to a block of mass 5 kg at rest, if it moves 36 m, in first 3 seconds. Neglect the force of friction.
Given: mass of block = m = 5 kg, Initial velocity = u = 0, Distance traveled = s = 36 m, time taken = t = 3 s,
To find: F =?
Solution:
s = ut + 1/2 at2
∴ 36 = (0)(3) + 1/2 a(3)2
∴ 36 = 1/2 a(9)
∴ 72 = a (9)
∴ a = 72/9 = 8 m/s2.
By Newton’s second law of motion, the magnitude of force
F = ma = 5 x 8 = 40 N
Ans: The force applied = 40 N
Example – 09:
Two spheres of mass 10 g and 100 g each fall on the two pans of a table balance from a height of 40 cm and 10 cm respectively. If both are brought to rest in 0.1 seconds. Determine the force exerted by each sphere on the pans.
Solution:
For the first sphere:
Given : m1 = 10 g = 0.01 kg, h = – 40 cm = – 0.4 m, t = 0.1 s, g = – 9.8 m/s2
v2 = u2 + 2gh
∴ v2 = (0)2 + 2(-9.8)(-0.4)
∴ v2 = 7.84
∴ v = 2.8 m/s
F1 = m1a
F1 = m1 (v – u)/t = 0.01 x (2.8 – 0)/0.1 = 0.28 N
For the second sphere:
Given : m1 = 100 g = 0.1 kg, h = – 10 cm = – 0.1 m, t = 0.1 s, g = – 9.8 m/s2
v2 = u2 + 2gh
∴ v2 = (0)2 + 2(-9.8)(-0.1)
∴ v2 = 1.96
∴ v = 1.4 m/s
F2 = m2a
F2 = m2 (v – u)/t = 0.1 x (1.4 – 0)/0.1 = 1.4 N
Ans: The force exerted by the first sphere is 0.28 N and that by second sphere is 1.4 N
Example – 10:
Calculate the density of a cubical ice block of side 50 cm. If a force of 1125 N applied to it produces an acceleration of 10 m/s2 in it. Neglect the force of friction. Assume the ice block remains in solid state without melting.
Given: Force applied = F = 1125 N, acceleration = a = 10 ms-1, Side of a block = 50 cm = 0.5 m
To Find: Density = ρ = ?,
Solution:
By Newton’s second law of motion
F = m.a
∴ 1125 = m x 10
∴ m = 1125/10 = 112.5 kg
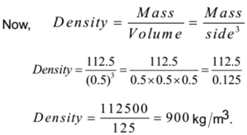
Ans: The density of ice block is 900 kg/m3.
Example – 11:
A ball of mass 50 g at rest is hit by a bat and the ball covers a distance of 400 m, in 2 seconds. If the ball was in contact with it for 0.1 s, find the magnitude of the force acting on it. Assuming no other force acts on a ball after it is hit by the bat.
Given: mass of ball = m = 50 g = 0.05 kg, time of contact = 0.1 s, distance covered s= 400 m, time taken to cover the distance = t = 2 s.
To find: Force acting =F =?
Solution:
No other force acts on a ball after it is hit by the bat. Thus it is in uniform motion after hit.
v = s/t = 400/2 = 200 m/s
Now Force, F = ma
F = m (v – u)/t = 0.05 x (200 – 0)/0.1 = 100 N
Ans: The force acting = 100 N
Example – 12:
A force of 500 N acts on a body of mass 1000 kg and the body is brought to rest within a distance of 64 m. Find the initial velocity and time taken by the body to come to rest.
Given: mass of body = m = 1000 kg, Force acting = F = 500 N, Final velocity = v = 0 ms-1, distance traveled = s = 64m.
To find: initial velocity =u =? time taken = t = ?
Solution:
We have F = ma
∴ 500 = 1000 x a
∴ a = 500/1000 = 0.5 m/s2
As the body is brought to rest a = – 0.5 m/s2
v2 = u2 + 2as
∴ (0)2 = u2 + 2(-0.5)(64)
∴ (0)2 = u2 – (64)
∴ u2 = 64
∴ u = 8 m/s
By first equation of motion
v = u + at
∴ 0 = 8 + (- 0.5) x t
∴ 8 = – 0.5 x t
∴ t = 8/0.5 = 16 s
Ans: Initial velocity = 8 m/s, time taken to come to rest = 16 s
Example – 13:
A car of mass 1000 kg is moving uniformly with 10 m/s. If the engine of the car develops an extra linear momentum of 1000 kg m/s. Calculate the new velocity with which the car runs.
Solution:
Given : mass of car = m = 100 kg, initial velocity = u = 10 m/s, Extra momentum = 1000 kg m/s,
To find: Final velocity = v = ?
Initial momentum = p1 = mu = 1000 x 10 = 10000 kg m/s
Final momentum = p2 = 10000 + 1000 = 11000 kg ms-1.
Now, Final momentum = p2 = mv
∴ 11000 = 1000 x v
∴ v = 11000/1000 = 11m/s
Ans: New Velocity = 11 m/s
Previous Topic: Applications of Newton’s Laws
Next Topic: Law of Conservation of Momentum
2 replies on “Simple Numerical Problems on Force”
Hi,this is so great site I think you all going to follow this site
I love this post and it really helped me