Source of Problems: Fundamentals of Physics by Halliday and Resnick, 10th Edition: Chapter 1: Problems 1 to 9
Example 01:
Earth is approximately a sphere of radius 6.37 x 106 m. What are (a) its circumference in kilometers, (b) its surface area in square kilometers, and (c) its volume in cubic kilometers?
Given: radius of earth = R = 6.37 × 106 m = 6.37 × 106 × 10-3 km = 6.37 × 103 km
To Find: Circumference = C =?, Surface area = A =?, Volume = V =?
Solution:
Circumference = C = 2 πR = 2 × 3.142 × 6.37 × 103 = 4.00 × 104 km
Surface Area = A = 4 π R2 = 2 × 3.142 × (6.37 × 103)2 = 5. 10 × 108 km2
Volume = 4/3 π R3 = (4/3) × 3.142 × (6.37 × 103)3 = 1.08 × 1012 km3
Ans: Circumference of earth = 4.00 × 104 km, Surface area of earth = 5. 10 × 108 km2, and Volume of earth = 1.08 × 1012 km3.
Example 02:
Gry is an old English measure for length, defined as 1/10 of a line, where the line is another old English measure for length, defined as 1/12 inch. A common measure for length in the publishing business is a point, defined as 1/72 inch. What is an area of 0.50 gry2 in points squared (points2)?
Given: 1 gry = 1/10of a line, 1 line = 1/12 inch, 1 point = 1/72 inch, Area = 0.50 gry2.
To Find: area in points2 =?
Solution:
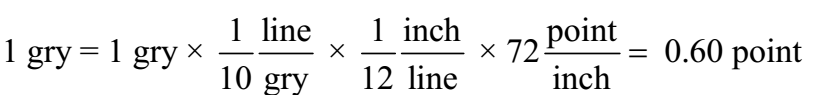
∴ 1 gry2 = (0.60 point) 2 = 0.36 point2
∴ 0.50 gry2 = 0.50 × 0.36 point2 = 0.18 point2
Ans: area of 0.50 gry2 is0.18 point2
Example 03:
The micrometer (1 μm) is often called the micron. (a) How many microns make up 1.0 km? (b) What fraction of a centimetre equals 1.0 μm? (c) How many microns are in 1.0 yd?
1. 0 km = 1 × 103 m = 1 × 103 × 106 μm = 109 μm
1.0 μm = 1 × 10-6 m = 1 × 10-6 × 102 cm = 10-4 cm
1.0 yd = 0.9144 m = 0.9144 × 106 μm = 9.1 × 105 μm
Ans: 1. 0 km = 109 μm, 1.0 μm = 10-4 cm, and 1.0 yd = 9.1 × 105 μm
Example 04:
Spacing in this book was generally done in units of points and picas: 12 points =1 pica, and 6 picas = 1 inch. If a figure was misplaced in the page proofs by 0.80 cm, what was the misplacement in (a) picas and (b) points?
Given: 12 points = 1 pica, and 6 picas = 1 inch, Misplacement = 0.80 cm
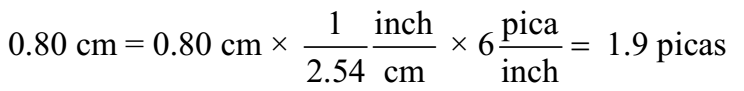
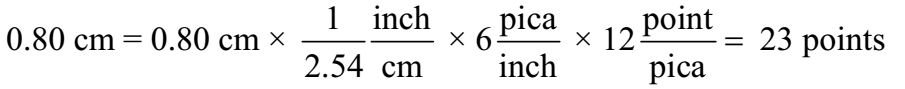
Ans: Misplacement of 0.80 cm corresponds to 1.9 picas or 23 points
Example 05:
Horses are to race over a certain English meadow for a distance of 4.0 furlongs. What is the race distance in (a) rods and (b) chains? (1 furlong = 201.168 m, 1 rod = 5.0292 m, and 1 chain = 20.117 m.)
Given: 1 furlong = 201.168 m, 1 rod = 5.0292 m, and 1 chain = 20.117 m, Distance = 4.0 furlongs
Solution:


Ans: Distance of 4.0 furlongs equals to 160 rods or 40 chains.
Example 06:
You can easily convert common units and measures electronically, but you still should be able to use a conversion table, such as those in Appendix D. Following table is part of a conversion table for a system of volume measures once common in Spain; a volume of 1 fanega is equivalent to 55.501 dm3 (cubic decimeters). To complete the table, what numbers (to three significant figures) should be entered in (a) the cahiz column, (b) the fanega column, (c) the cuartilla column, and (d) the almude column, starting with the top blank? Express 7.00 almudes in (e) medios, (f) cahizes, and (g) cubic centimeters (cm3).

Solution:
From table, 1 cahiz = 12 fanga
∴ 1 fanega = 1/12 = 8.33 x 10-2 cahiz
From table, 1 cahiz= 48 cuartilla
∴ 1 cuartilla = 1/48 = 2.08 x 10-2 cahiz

From table 1 cahiz = 144 almude
∴ 1 almude = 1/144 cahiz = 6.94 × 10-3 cahiz


From table 1 cahiz = 288 medio
∴ 1 medio = 1/288 = 3.47 × 10-3 cahizcahiz



∴ 1 medio = (3.47 × 10-3)/( 6.94 × 10-3) = 0.500 almude
Completed table is
| cahiz | fanega | cuartilla | almude | medio | |
| cahiz | 1 | 12 | 48 | 144 | 288 |
| fanega | 8.33 x 10-2 | 1 | 4 | 12 | 24 |
| cuartilla | 2.08 x 10-2 | 0.250 | 1 | 3 | 6 |
| almude | 6.94 x 10-3 | 8.33 x 10-2 | 0.333 | 1 | 2 |
| medio | 3.47 x 10-3 | 4.17 x 10-2 | 0.167 | 0.500 | 1 |
Part II:
1 almude = 2 medios
∴ 7.0 almudes = 7 × 2 = 14.0 medios
1 almude = 6.94 × 10-3 cahizes
∴ 7.0 almudes = 7 × 6.94 × 10-3 = 4.86 × 10-2 cahizes
1 almude = 8.33 × 10-2 fanega
7.0 almudes = 7 × 8.33 × 10-2 = 0.5831 fanega
Given 1 fanega = 55.501 dm3 = 55.501 x (10-1 m)3
1 fanega = 55.501 × 10-3 m3 = 55.501 × 10-3 × (102 cm)3
∴ 1 fanega = 55.501 × 10-3 × 106 cm3
∴ 1 fanega = 55.501 × 103 cm3
7.0 almudes = 0.5831 fanega = 0.5831 × 55.501 × 103 cm3
∴ 7.0 almudes = 3.24 × 104 cm3
Example 07:
Hydraulic engineers in the United States often use, as a unit of volume of water, the acre-foot, defined as the volume of water that will cover 1 acre of land to a depth of 1 ft. A severe thunderstorm dumped 2.0 in. of rain in 30 min on a town of area 26 km2. What volume of water, in acre-feet, fell on the town?
Solution:
Area = 26 km2 = 26 × (103)2 m2 = 26 × 106 m2
We know that 1 acre = 4046.86 m2

Area = 26 km2 = (26 x 106)/( 4046.86) = 6425 acre
Depth of water = 2.0 inch = 2/12 = 1/6 ft
∴ Volume of water = (6425) × (1/6) = 1071 = 1.1 × 103 acre-feet
Example 08:
Harvard Bridge which connects MIT with its fraternities across the Charles River, has a length of 364.4 Smoots plus one ear. The unit of one Smoot is based on the length of Oliver Reed Smoot, Jr., class of 1962, who was carried or dragged length by length across the bridge so that other pledge members of the Lambda Chi Alpha fraternity could mark off (with paint) 1-Smoot lengths along the bridge. The marks have been repainted biannually by fraternity pledges since the initial measurement, usually during times of traffic congestion so that the police cannot easily interfere. (Presumably, the police were originally upset because the Smoot is not an SI base unit, but these days they seem to have accepted the unit.) Figure shows three parallel paths, measured in Smoots (S), Willies (W), and Zeldas (Z). What is the length of 50.0 Smoots in (a) Willies and (b) Zeldas?

Solution:
From figure we can see that
212 S is equivalent to 258 W
Thus 1 S = (258/212) = 1.217 W

212−32 =1 80 S is equivalent to 216−60=156 Z.
Thus 1 S = 156/180 = 0.8667 Z

Ans: 50.0 Smoots is equivalent to 60.8 Willies or 43.3 Zeldas
Example 09:
Antarctica is roughly semicircular, with a radius of 2000 km (Fig. 1-5). The average thickness of its ice cover is 3000 m. How many cubic centimeters of ice does Antarctica contain? (Ignore the curvature of Earth.)

Given: Radius R = 2000 km = 2000 x 103 m =2000 x 103 x 102 cm = 2 x 108 cm, Depth of ice = Z = 3000 m = 3000 x 102 cm = 3 x 105 cm
To Find: Volume of ice = V=?
Solution:
Volume of ice = V = (1/2) × πR2 × z
∴ V = (1/2) × 3.142 × (2 x 108)2 × (3 x 105)
∴ V = (1/2) × 3.142 × 4 × 1016 × 3 × 105
∴ V = 1.9 × 1022 cm3
Ans: Volume of ice in Antarctica = 1.9 × 1022 cm3