Science > Physics > Force > Moment of Force
In this article, we shall study the concept of moment of force, its characteristics, and applications in everyday use.
Rigid Body:
A rigid body is one whose geometric shape and size remains unchanged under the action of an external force. In the rigid body, the distance between any two particles of the body remains constant. In other words the relative position of each particle w.r.t. any other particle always remains the same. If force is applied (whatever may be its magnitude) there is no change in the shape of the body. Although no perfectly rigid body exists, many bodies can be considered as rigid bodies for a practical purpose.
Rotational Motion and Axis of Rotation:
A rigid body is said to perform rotational motion when the particles lying on the straight line in the body remains stationary and all other particles move in circles around this straight line. The straight line inside the body which remains fixed is called the axis of rotation.
When a force is applied on a rigid body which is free to move, the body starts moving in a straight line in the direction of the force. The motion of the body is called linear or translational motion. But if the body is pivoted at a point, the force applied on the body at suitable point rotates the body about its fixed point.(or about the axis passing through the fixed point) This is called rotational motion. For example, when a force is applied at the handle of the door, the door rotates.
A single force can produce translational motion of a body if it is free to move, but a single force applied on a body fixed at a point does not cause rotational motion of the body.
Moment of Force:
In translational motion the linear acceleration of body depends on the force acting on the body, similarly, in rotational motion, angular acceleration depends on the moment of force or torque acting on the body. The ability of a force to produce rotational motion is measured in terms of the moment of force. Its magnitude about the given axis depends on the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation. This distance is called the moment arm.
The Magnitude of moment = force × moment arm
It is denoted by letter M. Its S.I. unit is N.m. Its dimensions are [m1L2T-2]. It is a vector quantity, whose direction is given by right-hand thumb rule.
Sign Convention Used for Moment of Force:
- If the force applied to the body rotates the body in an anticlockwise sense, then it is considered as positive.
- If the force applied to the body rotates the body in a clockwise sense, then it is considered as negative.
- The direction of the moment of force (torque) is given by right-hand rule. It states that “Encircle the axis of rotation by fingers of the right hand which point in the direction in which the body tends to rotate, then the thumb points in the direction of torque or moment of the force vector.
Expression for Moment of Force:
Consider a body of any shape capable of rotating about an axis passing through point O and perpendicular to the plane of paper as shown in the diagram
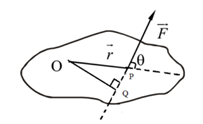
Let P be a point in the plane the f paper. Let r be the position vector of point P with respect to point O. Let F be the force acting at point P making an angle θ with position vector . In right-angled Δ PQO,
sin θ = OQ/OP
OQ = OP Sin θ = r Sin θ
The magnitude of the moment of force = Force × Moment arm
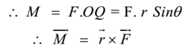
Thus the moment of force is a vector product of moment arm and the force. Its direction is given by right-hand thumb rule. In this case, the direction is perpendicular to the plane of the paper and towards us.
Scientific Reasons:
It is easy to open a door by applying the force at the free end.
The door rotates about an axis passing through its hinges.
Required moment of force to rotate the door = force x moment arm
When we apply force at the free end, the distance of the force from the axis of rotation (moment arm) is more. Thus less force is required to open the door due to a large turning effect.
The hand flour grinder is provided with a handle near its rim.
The upper stone of a flour grinder rotates about an axis passing through its centre.
Required moment of force to rotate the stone = force x moment arm
When the handle is near the rim, the distance of the force from the axis of rotation (moment arm) is more. Thus less force is required to rotate the stone of a flour grinder is less due to large turning effect.
A long handle spanner is used to loosen or tight nut.
During loosening or tightening the nut rotates about an axis passing through its centre.
Required moment of force to rotate the spanner = force x moment arm
When long handle spanner is used, the distance of the force from the axis of rotation (moment arm) is more. Thus less force is required to loosen or tight the nut due to large turning effect.
In bicycle long pedals are used.
In bicycle, the pedals are used to rotate the toothed wheel about an axis passing through its centre.
Required moment of force to rotate the wheel = force x moment arm
When long pedals are used, the distance of the force from the axis of rotation (moment arm) is more. Thus less force is required to rotate the toothed wheel due to large turning effect.
Principle of Moments:
If a body is in rotational equilibrium then the sum of the anticlockwise moments is equal to the sum of the clockwise moments. OR If a body is in rotational equilibrium then the algebraic sum of the moments about any point is zero.
Applications of Principle of Moments:
- To find the mass of an object
- In levers (Simple Machine)
Previous Topic: Elastic and Inelastic Collision
2 replies on “Moment of Force”
It is very good for me
great explanation!!!