Science > Physics > Motion in a Straight Line > Terminology of Motion
Motion is an important part of our life. Our daily activities involve motion of different kinds. In this topic, we shall study the terminology of motion.
- Mechanics: The branch of physics which deals with the effects of forces on object is called mechanics. Mechanics is further classified into dynamics and statics.
- A Point Object: In the study of Mechanics we consider bodies or objects as particles or point objects. An object is said to be a point object if its dimensions are negligible as compared to the distance travelled by it. For example distance between stars is so large that for practical purpose those stars can be considered as particles or point objects.
- Body in Motion: A body is said to be in motion if it changes its position with respect to its immediate surroundings. It is to be noted that the motion of a body is a relative concept.
- Body at Rest: A body is said to be at rest if it does not change its position with respect to its immediate surroundings.
- Dynamics: The branch of physics (mechanics) which deals with the motion of the bodies and the forces causing it is called dynamics. It is further classified into kinematics and kinetics.
- Kinematics: The branch of physics (mechanics) which deals with the motion of the bodies without considering the forces causing it is called kinematics.
- Kinetics: The branch of physics which deals with the motion of bodies considering cause of their motion.
- Statics: It is the branch of physics which deals with objects at rest under the action of forces.
Motion is a Relative Concept:
The motion of a body is a relative concept. When we are specifying the motion it is with respect to some observer. Let us consider to persons say A and B in a lift moving upward. There is another person C standing outside the lift. Now though the lift is going up for A and B there is no change in positions with respect to each other. Thus for A and B, there is no motion with respect to each other but for both of them, C is moving downward. Now for C both A and B are moving upward. Hence motion is relative.
With respect to the earth surface, we may be at rest but we are moving about 100,000 km hr-1 relative to sun.
Classification of Motion:
Motion can be classified into random motion, translational motion, rotational motion, and vibrational or oscillatory motion.
Random Motion:
In this motion particles move randomly in any possible direction and in any possible velocity. Thus, the path and the direction are not definite. Example: Motion of gas molecules. Such random motion of molecules of gas is called molecular chaos.
Translational Motion:
In this motion every particle of the body has the same displacement. The translational motion can be along straight line or along a curved path. Motion along a straight line is called a rectilinear motion (e.g. motion of car in a straight line) and the motion of a body along a curved path is called curvilinear motion (e.g. the motion of a ball thrown in air, the motion of the earth around the Sun).
Rotational Motion:
In this motion the particles of body revolve in a circle about the same axis. Examples: Motion of a fan, the motion of a wheel of moving vehicle, the motion of merry go round, etc.
Oscillatory or Vibrational Motion:
In this motion the body moves to and fro about a fixed point along the same path. Examples: The motion of the bob of a pendulum, vibrating string of guitar, etc.
Rectilinear Motion or One Dimensional Motion:
When a body moves along a straight-line path, its motion is called the one-dimensional motion or motion in a straight line or rectilinear motion. Example: the motion of a car along a straight road.
The Position of a Body or Particle:
Assuming the direction of the motion along the x-axis, the path of one-dimensional motion can be represented by a straight line parallel to the x-axis then each point on the straight line represents the position of the particle at a different instant of time. The position of the particle at any instant can be specified by its x-coordinate. The x-coordinate changes with time.
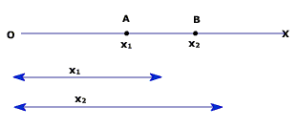
Distance and Displacement:
Distance:
The length of the path travelled by a body is called the distance travelled by it. The path of a body may not be straight. Distance is also referred as path length.
It is denoted by ‘s’ or ‘x’. Its S.I. unit is metre (m) and the c.g.s. unit is centimetre (cm). Its dimensions are [L1M0T0]
Characteristics of Distance:
- It is the length of the path followed by the object in a certain time. The path followed may or may not be along a straight line.
- It is a scalar quantity.
- It depends on the path followed by the object.
- It is always positive.
- It can be more than or equal to displacement.
- It may not be zero even if the displacement is zero.
Displacement:
The shortest distance from the initial position to the final position of the body is called the magnitude of the displacement.
It is a vector quantity whose direction is from initial position to final position. Its S.I. unit is metre (m) and the c.g.s. unit is centimetre (cm). Its dimensions are [L1M0T0]
Characteristics of Displacement:
- It is the shortest distance between the initial position to the final position of the body. It is always along a straight line.
- It is a vector quantity whose direction is from the initial position to final position.
- It is independent of the path followed by the object.
- It may be positive, negative or zero.
- It may be equal but cannot be more than the distance travelled.
- It is zero when the distance travelled is zero.
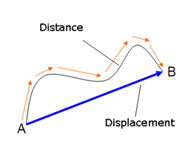
Displacement May be Positive or Negative or Zero.
Case – 1: When Distance travelled and displacement are equal.
If an object moves along the positive direction of the x-axis through 4m and further moves by 3 m in the same direction. In this case, the distance travelled by the object is 7m and displacement is also 7 m.

Case – 2: When Distance travelled and displacement are not equal and displacement is positive
If an object moves along the positive direction of the x-axis through 4m and further moves by 3 m in the opposite direction. In this case, the distance travelled by the object is 7m and displacement is also + 1 m (along the positive direction of the x-axis).

Case – 3: When Distance travelled and displacement are not equal and displacement is negative
If an object moves along the positive direction of the x-axis through 3m and further moves by 4 m in the opposite direction. In this case, the distance travelled by the object is 7m and displacement is also – 1 m (along the negative direction of the x-axis).

Case – 4: When Distance travelled and displacement are not equal and displacement is zero
If an object moves along the positive direction of the x-axis through 4m and further moves by 4 m in the opposite direction. In this case, the distance travelled by the object is 8 m and the displacement is also 0 m.

Understanding Concept of Displacement with Examples:
Example 01:
A cop gets information that a thief is 10 km away from the police station. Is it possible for cop to trace the thief with the given information?

This information is not sufficient as the direction in which the cop has to trace is not mentioned. The cop has to move along a circumference of a circle of radius 10 km through each and every point. At point T he can nab the thief. Thus, only specifying that a thief is 10 km away from the police station is not sufficient and it makes the task almost impossible. To trace the thief effectively with the distance direction also should be specified.
Thus for displacement both the magnitude and the direction is required. It is a vector quantity.
Example 02:
A horse is tied to a rope of length ‘r’ and the other end of the rope is tied to a pole. Find the displacement and the distance travelled by the horse in the following cases:
- When the horse makes half revolution along a circular path.
- When it makes one full revolution.
- When it makes 3/4 th of the revolution.
When the horse makes half revolution along a circular path.

The starting point of journey is P and the end point is at Q
Distance travelled = Circumference/2 = 2πr/2 = πr units
Displacement = PQ = r + r = 2r units
When it makes one full revolution.

The starting point of journey is P and the end point is at Q
Distance travelled = Circumference = 2πr units
Displacement = PQ = 0 units
When it makes 3/4 th of the revolution.

The starting point of journey is P and the end point is at Q
Distance travelled = 3/4 x Circumference = 3/4(2πr) = 3πr/2 units
Applying Pythagoras theorem to Δ POQ
Displacement = PQ = √2 r units
Distinguishing Between Distance and Displacement:
| Distance | Displacement |
| The length of the path travelled by a body is called the | The shortest distance from the initial position to the final position of the body is called the magnitude of the displacement. |
| The distance travelled by the body can be more than or equal to displacement. | Displacement can never be greater than the distance travelled by the body. |
| Distance depends upon the path followed and hence can have multiple values. | The displacement depends on the initial and the final position of the body and hence is single-valued. |
| Distance is a scalar quantity. | Displacement is a vector quantity. |
Speed:
The rate of change of distance with time is called the speed of the body.
Mathematically, speed = Distance/Time
It is denoted by v. Its S.I. unit is m/s and c.g.s. unit is cm/s. Its dimensions are [L1M0T-1].
Uniform Speed:
A body is said to move with uniform speed if it covers equal distances in equal intervals of time throughout its motion.
Non-Uniform or Variable Speed:
A body is said to move at a non-uniform speed if it covers unequal distances in the same intervals of time.
Instantaneous Speed:
When a speed of a body changes continuously with time, its speed at any instant is known as instantaneous speed.
Average Speed:
The ratio of the total distance travelled by the body to the total time of the journey is called average speed.
When a body is moving with uniform speed, then the instantaneous speed and average speed are equal.

Characteristics of Speed:
- The rate of change of distance with time is called the speed of the body.
- It is a scalar quantity
- Speed is always positive.
- In a circular motion, after executing a complete circle, the average velocity of the body is zero but its average speed is not zero.
Velocity:
The rate of change of displacement of a body with respect to time is called the velocity of the body.

Velocity is a vector quantity, its S.I. unit is m/s and c.g.s. unit is cm/s.Its dimensions are [L1M0T-1]
Uniform Velocity:
When the magnitude and direction of the velocity of a body remain the same at any instant, then the body is said to have uniform velocity. For uniform motion acceleration a = 0 and Displacement = velocity × time.
Example: The velocity of light in a particular medium is uniform velocity. The velocity of sound in air at constant temperature is uniform velocity.
Non Uniform Velocity:
When the magnitude of velocity or the direction of velocity or both changes at any instant the body is said to have the nonuniform velocity or variable velocity.
A body can have non-uniform velocity in the following three cases.
- When the direction of the velocity of a body remains the same but its magnitude changes continuously then the body has variable velocity. e.g. a ball is thrown vertically upward.
- When the magnitude of the velocity of a body remains the same but the direction changes continuously then the body has variable velocity. e.g. uniform circular motion of a body.
- When both the magnitude and direction of the velocity of body change continuously, then the body has variable velocity. e.g. ball thrown by making the acute angle with the horizontal (projectile motion)
When a body has variable velocity, then it has acceleration.
Instantaneous Velocity:
For a body moving with non-uniform velocity, the velocity of the body at an instant is called instantaneous velocity.
Average Velocity:
If the velocity of a body moving in particular direction changes with time, then the ratio of displacement to total time is called average velocity.
Characteristics of Velocity:
- The rate of change of displacement of a body with respect to time is called as the velocity of the body.
- It is a vector quantity.
- The velocity can be positive, negative or zero.
- In a circular motion, after executing a complete circle, the average velocity of the body is zero but its average speed is not zero.
Acceleration:
The rate of change of velocity with respect to time is called acceleration.

Acceleration is vector quantity its S.I. unit is m/s2. Its dimensions are [L1M0T-2].
Acceleration can be positive, negative or zero. If the velocity is increasing then acceleration is positive. If the velocity is decreasing acceleration is negative. If the velocity is the constant acceleration is zero. Negative acceleration is also called deceleration or retardation.
If the velocity is increasing then the direction of acceleration is same as that of the velocity of the body. If the velocity is decreasing then the direction of acceleration is opposite to that of the velocity of the body.
It is to be noted that the velocity and not the acceleration of the body determines the direction of motion.
Uniform Acceleration:
When equal changes take place in the velocity of a body in equal interval of time, then the acceleration is called uniform acceleration. e.g. the motion under gravity.
Variable Acceleration:
When The change in the velocity of a body in equal interval of time is not constant, then the acceleration is called non-uniform acceleration.
Acceleration Due To Gravity:
When the body falls freely under gravity, the acceleration produced in the body due to the gravitational force of attraction of the earth, then the acceleration by which the body falls down is called the acceleration of gravity.
It is denoted by ‘g’. Its value is g = 9.8 m/s2. When solving problems on the motion under gravity as per the convention the value of ‘g’ should be negative.
Next Topic: Numerical Problems on Displacement and Average Velocity
One reply on “Terminology of Motion”
I really appreciate this website because most conceptual things i see here