Newton’s Equations of Motion

Science > Physics > Motion in a Straight Line > Newton’s Equations of Motion

In this article, we shall study to solve problems based on Newton’s equations of motion.

First Equation of Motion:

Let u =  initial velocity of a body, v =   final velocity of the body

t = time in which the change in velocity takes place.

By the definition of acceleration

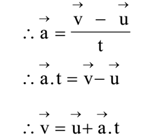
Considering magnitudes only

v = u + at

This equation is known as Newton’s First equation of motion.

Second Equation of Motion:

Let u =  initial velocity of a body, v =   final velocity of the body

t = time in which the change in velocity takes place, a = acceleration of the body

This equation is known as Newton’s second equation of motion.

Third Equation of Motion:

Let u =  initial velocity of a body, v =   final velocity of the body

t = time in which the change in velocity takes place.

from equation (1) and (2)

Considering the magnitude only

v² = u² = 2 a s

This equation is known as Newton’s third equation of motion.

Expression for the Distance Travelled by Body in nth Second of its Motion:

By Newton’s Second equation of motion, s = ut + ½  at²

where s = displacement of body in ‘t’ seconds

u = initial velocity of the body, a = acceleration of the body, t = time

The distance travelled by body in ‘n’ seconds is given by

This distance by travelled by the body in (n-1) seconds is given by

∴ The distance travelled by the body in n th second

Motion Under Gravity:

A special case of uniform acceleration is the motion of a body under gravity. It is found that close to the surface of the earth, and in the absence of air resistance, all the bodies fall to the earth, at a given place, with the constant acceleration.  This constant acceleration is called acceleration due to gravity or gravitational acceleration.

It is denoted by “g”. It is always directed downward.  Its magnitude is approximately 9.8 m/s². For the motion of a body under gravity Newton’s equations of motion can be written as

Sign Convention (Cartesian):

• All vectors directed towards the right of the reference point are considered positive.
• All vectors directed towards the left of the reference point are considered negative.
• All vectors directed vertically upward the reference point are considered positive.
• All vectors directed vertically downward the reference point are considered negative.
• By this sign convention acceleration due to gravity “g” is always negative.

Numerical Problems:

Example – 01:

A car acquires a velocity of 72 kmph in 10 s starting from rest. Calculate its average velocity, acceleration and distance travelled during this period.

Given: Initial velocity = u = 0, Final velocity = v = 72 kmph = 72 x 5/18 = 20 m/s, Time taken = t = 10 s

To Find: average velocity = v_av =?, acceleration = a =?, distance travelled = s =?

Solution:

v_av = (u + v) /2 = (0 = 20)/2 = 10 m/s

Average velocity is 10 m/s

By first equation of motion we have

v = u + at

∴    20 = 0 + a x 10

∴    a = 20/10 = 2 m/s²

acceleration = 2 m/s²

By second equation of motion

s = ut + ½ at² = 0 x (10) + ½ x 2 x (10)² = 0 + 100 = 100 m

distance travelled = 100 m

Ans: Average velocity = 10 m/s, acceleration = 2 m/s² , distance travelled = 100 m

Example – 02:

A ball is moving with a velocity of 0.5 m/s. Its velocity is decreasing at the rate of 0.05 m/s². What is its velocity after 5 s? How much time will it take from start to stop? What is the distance travelled by it before stopping?

Given: Initial velocity = u = 0.5 m/s, acceleration = a = – 0.05 m/s²

To Find:  a) v = ? when t = 5 s b) t = ? when v = 0, c) distance travelled = s = ?

Solution:

By first equation of motion  (v = ? when t = 5)

v = u + at  = 0.5 + (- 0.05) x 5  = 0.5 – 0.25 = 0.25 m/s

Thus the velocity of ball after 5 s is 0.25 m/s

By First equation of motion (t = ? when v = 0)

v = u + at

∴    0 = 0.5 + (- 0.05) x t

∴    0.5  = – 0.05 x t

∴    t = 0.5/0.05 = 10 s

The ball will stop after 10 s from start

By the second equation of motion

s = ut + ½ at² = 0.5 x (10) + ½ x (-0.05) x (10)² = 5 – 2.5 = 2.5 m

The ball travels 2.5 m before coming to rest.

Ans: Velocity after 5 seconds = 0.25 m/s, time taken to come to rest = 10 s, distance travelled before coming to rest = 2.5 m

Example – 03:

A car initially at rest starts moving with acceleration 0.5 m/s² covers a distance of 25 m. Calculate the time required to cover this distance and the final velocity of the car.

Given: Initial velocity = u = 0 m/s, acceleration = a = 0.5 m/s², distance travelled = s = 25m.

To Find:  time taken = t =? , final velocity = v = ?

Solution:

By the second equation of motion

s = ut + ½ at²

∴     25 = 0 x (t) + ½ x (0.5) x t²

∴    25 = 0.25 t²

∴    t² = 25/ 0.25 = 100

∴    t = 10 s

Time required by car to cover distance of 25 m is 10 s

By first equation of motion

v = u + at  = 0 + ( 0.5) x 10  = 5 m/s

The final velocity of ball after is 5 m/s.

Ans: Time required to cover the distance = 10s, final velocity = 5 m/s

Example – 04:

A body starts from rest with a uniform acceleration of 2 m/s². Calculate the distance travelled by the body in 2 s.

Given: Initial velocity = u = 0 m/s, acceleration = a = 2 m/s², time taken = t = 2 s.

To Find:  Distance travelled = s =?

Solution:

By the second equation of motion

s = ut + ½ at² = 0 x (2) + ½ x (2) x 2²  = 4 m

Ans: The distance travelled by the body is 4 m

Example – 05:

A body is moving with 5m/s is accelerated at 5 m/s². Calculate the distance travelled by the body in 5 s.

Given: Initial velocity = u = 10 m/s, acceleration = a = 5 m/s², time taken = t = 5 s.

To Find:  Distance travelled = s =?

Solution:

By the second equation of motion

s = ut + ½ at² = 10 x (5) + ½ x (5) x 5²  = 50 + 62.5= 112.5 m

Ans: The distance travelled by the body is 4 m

Example – 06:

A vehicle is moving at a velocity of 30 kmph at some instant. After 2 s its velocity is found to be 33.6 kmph and after further 2 s the velocity is found to be 37.2 kmph. find the acceleration of the vehicle and comment on the result.

Solution:

Consider the change of velocity from 30 kmph to 33.6 kmph in 2 s.

u = 30 kmph = 30 x 5/18 = 150/18 m/s, v = 33.6 kmph = 33.6 x 5/18 = 168/18 m/s, t = 2 s

By first equation of motion

v = u + at

168/18 = 150/18 + a(2)

168/18 – 150/18 = 2a

2a = 18/18 = 1

a = 1/2 = 0.5 m/s²

Consider the change of velocity from 33.6 kmph to 37.2 kmph in 2 s.

u = 33.6 x 5/18 = 168/18 m/s, v = 37.2 kmph = 37.2 x 5/18 = 186/18 m/s, , t = 2 s

By first equation of motion

v = u + at

186/18 =  168/18 + a(2)

186/18 – 168/18 = 2a

2a = 18/18 = 1

a = 1/2 = 0.5 m/s²

Ans: The acceleration is same in both the cases thus the vehicle is moving with a constant acceleration of 0.5 m/s².

Example – 07:

A body initially at rest travels a distance of 100 m in 5 s with constant acceleration. calculate the acceleration and the final velocity at the end of 5 s.

Given: Initial velocity = u = 0 m/s, time taken = t = 5 s, distance travelled = s = 100 m

To Find:  Acceleration = a =?, final velocity = v =?

Solution:

By the second equation of motion

s = ut + ½ at²

100 = 0 x (5) + ½ x (a) x 5² 

200 = 25 a

a = 200/25 = 8 m/s²

Acceleration = 8 m/s²

By first equation of motion

v = u + at

v = 0 + 8 x 5 = 40 m/s

Ans: Acceleration = 8 m/s² and Final velocity = 40 m/s

Example – 08:

A body initially at moving with a speed of 18 kmph is accelerated uniformly at the rate of 9 cm/s² covers a distance of 200 m. Calculate the final velocity.

Given: Initial velocity = u = 18 kmph = 18 x 5/18 = 5 m/s, distance travelled = s = 100 m, acceleration = 9 cm/s² = 0.09 m/s².

To Find:  final velocity = v =?

Solution:

By the third equation of motion

v²  = u²  + 2as

v²  = 5²  + 2 x 0.09 x 200 = 25 + 36

v²  = 61

v = 7.81 m/s

Ans: The final velocity = 7.81 m/s

Example – 09:

A body initially at rest starts accelerating at the rate of 2 m/s². Find the final velocity and distance travelled by the body after 5s.

Given: Initial velocity = u = 0 m/s, acceleartion = a = 2 m/s², time taken = t = 5 s

To Find:  distance travelled = ?, final velocity = v =?

Solution:

By the second equation of motion

s = ut + ½ at² = 0 x 5 + ½  x 2 x 5² =  25 m

Distance travelled = 25 m

By first equation of motion

v = u + at

v = 0 + 2 x 5 = 10 m/s

Final velocity = 10 m/s

Ans: The final velocity = 10 m/s and distance travelled = 25 m

Example – 10:

A train moving with a velocity 72 kmph is brought to rest by applying brakes in 5 s. Calculate the retardation and distance travelled during this period.

Given: Initial velocity = u = 72 kmph = 72 x 5/18 = 20 m/s, final velocity = v = 0 m/s, time taken = t = 5 s

To Find:  distance travelled = ?, retardation = a =?

Solution:

By first equation of motion

v = u + at

0 = 20 + a x 5

5a = -20

a = -20/5 = -4 m/s²

Neagative sign indicates retardation

retardation = 4 m/s²

By the second equation of motion

s = ut + ½ at² = 20 x 5 + ½  x (- 4) x 5² =  100 – 50 = 50 m

Distance travelled = 50 m

Example – 11:

A body moves from rest with uniform acceleration and travels 270 m in 3 s. Find the velocity of the body after 5 s..

Given: Initial velocity = u = 0 m/s, distance travelled  = s = 270 m, time taken = t = 3 s

To Find:  velocity = ? when t = 5 s.

Solution:

By the second equation of motion

s = ut + ½ at²

270 = 0 x 5 + ½  x (a) x 3²

270 = 9/2 a

a = 540/9 = 60 m/s²

By first equation of motion

v = u + at  = 0 + 60 x 5 = 300 m/s

Ans: The velocity after 5s is 300 m/s

Example – 12:

A body moving with constant acceleration travels the distances 3 m and  8 m in 1 s and 2 s respectively. Calculate the initial velocity and acceleration of the body

Given:  Case – 1:  distance travelled  = s₁ = 3 m, time taken = t₁ = 1 s, Case – 2: distance travelled  = s₂ = 8 m, time taken = t₂ = 2 s,

To Find:  initial velocity = u = ? acceleration = a =?

Solution:

By the second equation of motion

s = ut + ½ at²

For first case

3 = u x 1 + ½  x (a) x 1²

3 = u + ½  x (a)

2u + a = 6 ……. (1)

For second case

8 = u x 2 + ½  x (a) x 2²

8  = 2u + 2 a

u + a = 4 ……. (2)

Solving equations (1) and (2) simultaneously

a = 2  and u = 2

Ans: Initial velocity = 2 m/s and acceleration = 2 m/s².

Example – 13:

A body moving with constant acceleration travels the distances 84 m and  264 m in 6 s and 11 s respectively. Calculate the initial velocity and acceleration of the body

Given:  Case – 1:  distance travelled  = s₁ = 84 m, time taken = t₁ = 6 s, Case – 2: distance travelled  = s₂ = 264 m, time taken = t₂ = 11 s,

To Find:  initial velocity = u = ? acceleration = a =?

Solution:

By the second equation of motion

s = ut + ½ at²

For first case

84 = u x 6 + ½  x (a) x 6²

84 = 6u + 18a

u + 3a = 14 ……. (1)

For second case

264 = u x 11 + ½  x (a) x 11²

264 = 11u + ½  x (a) x 121

22u + 121a = 528

2u + 11a = 48 ……. (2)

Solving equations (1) and (2) simultaneously

a = 4  and u = 2

Ans: Initial velocity = 2 m/s and acceleration = 4 m/s².

Example – 14:

A bus is moving with uniform velocity. The driver of the bus sees a pedestrian crossing the road at a distance of 60 m from the bus. He applied the brakes and reduce the speed with retardation of 25 cm/s2 and takes 20 s to stop the bus. Find the initial velocity of the bus and also decide the fate of the pedestrian.

Solution:

Given:  acceleration = – 25 cm/s² = – 0.25 m/s², time taken = t = 20 s, Final velocity = 0 m/s.

To Find:  initial velocity = u = ? Distance travelled = s = ?

By first equation of motion

v = u + at

0 = u + (-0.25)(20)

0 = u – 5

u = 5 m/s

Initial velocity = u = 5 m/s

By the second equation of motion

s = ut + ½ at²

s = 5 x 20 + ½  x (-0.25) x 20² = 100 – 50 = 50 m

As the distance travelled by the bus is less than the distance of pedestrian from the bus, there will be no accident

Example – 15:

A train is moving with a velocity of 90 kmph. When the brakes are applied the acceleration is found to be 0.5 m/s². Find the velocity after 10 s, the time taken to stop and the distance traveled before stopping from the application of brakes.

Given:  acceleration = – 0.5 m/s², time taken = t = 20 s, initial velocity = u = 90 kmph = 90 x 5/18 = 25 m/s.

To Find:  velocity = v = ? when t = 10 s, time taken = ? when v = 0,  Distance travelled = s = ?

Solution:

By first equation of motion

v = u + at  = 25 + (-0.5)(10) = 25 – 5 = 20 m/s

Velocity after 10 s is 20 m/s

By first equation of motion

v = u + at

0 = 25 + (-0.5)(t)

25 = – 0.5 t

t = 25/0.5 = 50 s

The train will take 50 s to stop

Velocity after 10 s is 20 m/s

By the second equation of motion

s = ut + ½ at²

s = 25 x 50 + ½  x (-0.5) x 50² = 1250 – 625 = 625 m

Ans: The train will civer 625 m before coming to rest

Example – 16:

A train is moving with a velocity of 54 kmph. It is accelerated at the rate 5 m/s². Find the distance travelled by the train in 5 seconds and in the  5th second of its journey.

Given:  acceleration = 5 m/s², time  = t = 5 s, initial velocity = u = 54 kmph = 54 x 5/18 = 15 m/s.

To Find:  Distance travelled in 5 s =? and distance travelled in 5th second = ?

Solution:

By the second equation of motion

s = ut + ½ at²

s = 15 x 5 + ½  x (5) x 5² = 75 + 62.5 = 137.5 m

Distance travelled in 5 s is 137.5 m

The distance travelled in nth second is given by

s_n = u +1/2a(2n – 1)

s₅ = 15 +1/2x 5 x (2 x 5 – 1)  = 15 +2.5 x 9

s₅ = 15 + 22.5 = 37.5 m

Ans: The distance travelled in 5 seconds = 137.5 m and the distance travelled in 5th second is 37.5 m

For More Topics in Motion in Straight Line Click Here

For More Topics in Physics Click Here

Science > Physics > Motion in a Straight Line > Newton’s Equations of Motion