In this article, we shall study to solve numerical problems based on simple pendulum.
Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on a Simple Pendulum
Example – 01:
The period of oscillation of a simple pendulum is 1.2 sec.in a place where g= 9.8m/s2. How long is the bob below the rigid point?
Given: Period = T = 1.2 s, g = 9.8m/s2.
To Find: Length of pendulum = l =?
Solution:
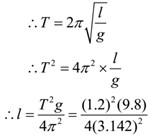
∴ l = 0.36 m
Ans: The bob is 0.36 m below the fixed point.
Example – 02:
If the period of oscillations of a simple pendulum is 4 s, find its length. If the velocity of the bob in the mean position is 40 cm/s, find its amplitude. g= 9.8 m/s2.
Given: Period = T = 4 s, velocity at mean position = vmax = 40 cm/s, g = 9.8m/s2.
To Find: Length of pendulum = l = ? amplitude =?
Solution:
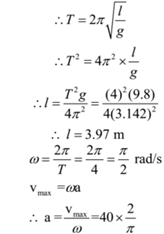
∴ a = 25.5 cm
Ans: The length of the pendulum is 3.97 m and amplitude is 25.5 cm
Example – 03:
A simple pendulum of length 1 m has a mass of 10 g and oscillates freely with an amplitude of 2 cm. Find its PE at the extreme point. g = 9.8 m/s2.
Given: Length of pendulum = l = 1 m, mass of bob = m = 10 g = 0.010 kg, amplitude = a = 2 cm = 0.02 m, g = 9.8m/s2.
To Find: Potential energy at extreme point = EP =?
Solution:

Ans: Potential energy at the extreme point is 1.96 x 10-5 J
Example – 04:
Calculate the maximum velocity at which an oscillating pendulum of length one meter will attain if its amplitude is 8 cm. g = 9.8 m/s2.
Given: length of pendulum = l = 1 m, amplitude = a = 8 cm.
To Find: Maximum velocity = vmax =?
Solution:

vmax = ωa = 3.13 x 8 = 25.04
Ans: maximum velocity is 25.04 cm/s
Example – 05:
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length and period of pendulum. g = 9.8 m/s2
Given: l 2 m = l 1 m – 20 cm = (l 1 – 0.20) m, g = 9.8m/s2.
To Find: original length and period =?
Solution:

0.81 l = l – 0.20
l – 0.81 l = 0.20
0.19 l = 0.20
l = 0.20/0.19 = 1.05 m
Ans: Original length is 1.05 m and original period is 2.06 s.
Example – 06:
When the length of a simple pendulum is increased by 22 cm, the period changes by 20% .Find the original length of simple pendulum. g= 9.8 m/s2
Given: l 2 m = l 1 m + 22 cm = (l 1 + 0.22) m, g = 9.8 m/s2. period change = 20%
To Find: original length and period = ?
Solution:

1.44 l = l + 0.22
1.44 l – l = 0.22
0.44 l = 0.22
l = 0.22/0.44 = 0.5 m
Ans: Original length is 0.5 m.
Example – 07:
The time of complete oscillation of a pendulum is doubled when the length of the pendulum is increased by 90 cm. Calculate the original length and original time of oscillation. g= 9.8 m/s2.
Given: l 2 m = l 1 m + 90 cm = (l 1 + 0.90) m, g = 9.8m/s2, T2 = 2T1.
To Find: original length and period = ?
Solution:

4 l = l + 0.90
4 l – l = 0.90
3 l = 0.90
l = 0.90/3 = 0.30 m= 30 cm

Ans: Original length is 30 cm. original period is 1.10 s
Example – 08:
The period of a simple pendulum at a place increases by 50%, when its length is increased by 0.6 m. Find its original length.
Given: l 2 = l 1 + 0.6 m, g = 9.8 m/s2.
To Find: original length = ?
Solution:

2.25 l = l + 0.6
2.25 l – l = 0.6
1.25 l = 0.6
l = 0.6/1.25 = 0.48 m
Ans: Original length is 0.48 m.
Example – 09:
The length of a seconds pendulum on the surface of the earth is one meter. What would be the length of a seconds pendulum on the surface of the moon where the acceleration due to gravity is g/6?
Given: Length on seconds pendulum on earth lE = 1m, gE = g anf gM = g/6.
To Find: length of second’s pendulum on the Moon = ?
Solution:

Ans: Length of seconds pendulum on the Moon is 1/6 m
Example -10:
What should be the length of a simple pendulum on the surface of the moon if its period does not differ from that on the surface of the earth? Mass of earth is 80 times that of the moon and radius of the earth is 4 times that of the moon.
Given: MM = 1/80 ME, RM = ¼ RE, TM = TE = constant.
To Find: Length of the pendulum on moon =?
Solution:


Ans: The length of the pendulum on the moon is 1/5th of length pendulum on the earth.
Example – 11:
The mass and diameter of a planet are twice of the earth. What will be the period of oscillations of a pendulum on this planet if it is a seconds pendulum on earth?
Given: MP = 2 ME, RP = 2 RE, lM = lE = constant, TE = 2 s.
To Find: Period of the pendulum on the planet = ?
Solution:


Ans: The period of the pendulum on the planet is 2.828 m.
Example – 12:
A pendulum takes 5 minutes for 100 oscillation at a place X. It takes the same time for 99 oscillations at another place Y. Compare the values of g at two places.
Given: Time period at place X = TX = 5min/ 100 oscillations = 5 x 60/100 = 300/100 s, Time period at place Y = TY = 5min/ 99 oscillations = 5×60/99 = 300/99 s,
To Find: Ratio of g at two places gX: gY=?
Solution:


Ans: The ratio of g at the two places is 1.02:1
Example – 13:
A clock regulated by a seconds pendulum keeps correct time. During summer the length of the pendulum increases to 1.01 m. How much will the clock gain or lose in one day? g= 9.8 m/s2.
Given: l1 = 1m, l2 = 1.01 m , T1 = 2 s.
To Find: Number of oscillations gain or lost =?
Solution:

Now the change in period = T2 – T1 = 2.017 – 2 = 0.017 s
For 2 seconds there is a decrease in 0.017 s
For 24 hours (24 x 60 x 60) the change is 0.017 x 24 x 60 x 60 /2 = 728.2 s
Ans: A clock will Lose 728.2 s per day
Example – 14:
A clock pendulum of period one second has given a correct time when the length of the pendulum is 0.36 m. If the length of the pendulum is increased by 0.13 m, how much time will the clock gain or lose in 24 hours? g=9.8 m/s2 .
Given: l1 = 0.36 m, l2 = 0.36 + 0.13 = 0.49 m ,
To Find: Number of oscillations gain or lost = ?
Solution:

Now the change in period = T2 – T1 = 1.405 – 1.204 = 0.201 s
For 1.204 seconds there is the increase of 0.201 s
For 24 hours (24 x 60 x 60) the change is 0.201 x 24 x 60 x 60 /1.204 = 14423 s = 4 hr
Ans: A clock will lose 4 hours per day
Example – 15:
If the length of the second’s pendulum is decreased by 0.5% how many oscillations will it gain or lose in a day?
Given: l2 = l1 – 0.5 % l1 = 0.995 l1 , T1 = 2 s.
To Find: Number of oscillations gain or lost =?
Solution:

T2 = 0.9975 T1 = 0.9975 x 2 = 1.995 s
Now the change in period = T1 – T2 = 2 – 1.995 = 0.005 s
For 2 seconds there is decrease of 0.005 s
For 24 hours (24 x 60 x 60) the change is 0.005 x 24 x 60 x 60 /2 = 216 s
Number of ocillations gained = 1/216 per second
Previous Topic: Theory of Simple Pendulum
Next Topic: Vibrations of Vertical springs
4 replies on “Numerical Problems on a Simple Pendulum”
Thanks it’svery helpful for me..
For preparation of bhu class 11 enterance exam
This was really helpful
It helps to much me for self study and making note. It also helps to improve my nuberical questions.
At last, I will give suggestions please also kept new model question sets of 2018 class 12.
it was not helpful for me bacause i didn’t want that types of numerical but all the numerical was so easy plz provide some difficult numerical problem related to pendulum clock for class 11