Science > Physics > Simple Machines > Numerical Problems on Levers
Example 01:
In a lever, the effort arm is 60 cm and load arm is 40 cm. Find its mechanical advantage:
Given: Effort arm = E.A. = 60 cm, Load arm = L.A. = 40 cm
To Find: Mechanical advantage = M.A. =?
Solution:
M.A. = E.A. / L.A. = 60 /40 = 1.5
Ans: Mechanical advantage of lever is 1.5
Example 02:
A crowbar of length 120 cm has its fulcrum situated at a distance of 20 cm from the load. Calculate the mechanical advantage of the crowbar.
Crowbar is class I lever
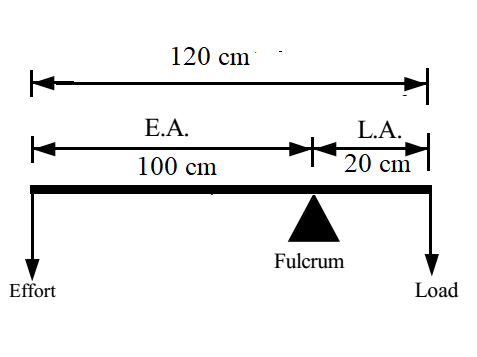
Given: Effort arm = E.A. = 100 cm, Load arm = L.A. = 20 cm
To Find: Mechanical advantage = M.A. =?
Solution:
M.A. = E.A. / L.A. = 100 /20 = 5
Ans: Mechanical advantage is 5
Example 03:
A pair of scissors has its blades 15 cm long, while its handles are 7.5 cm long. Find its mechanical advantage:
Given: Effort arm = E.A. = 7.5 cm, Load arm = L.A. = 15 cm
To Find: Mechanical advantage = M.A. =?
Solution:
M.A. = E.A. / L.A. = 7.5 /15 = 0.5
Ans: Mechanical advantage of is 0.5
Example 04:
A pair of scissors has its blades 15 cm long, while its handles are 7.5 cm long. Find its mechanical advantage:
Given: Effort arm = E.A. = 7.5 cm, Load arm = L.A. = 15 cm
To Find: Mechanical advantage = M.A. =?
Solution:
M.A. = E.A. / L.A. = 7.5 /15 = 0.5
Ans: Mechanical advantage of is 0.5
Example 05:
If the mechanical advantage of a lever is 10, Find the effort required to lift a box weighing 2500 N?
Given: Mechanical advantage = M.A. = 10, Load = W = 2500 N
To Find: Effort = P =?
Solution:
M.A. = W/P
P = W/M.A. = 2500/10 = 250 N
Ans: Effort required is 250 N
Example 06:
If a lever has a mechanical advantage of 0.5, and a person weighing 600 N sat on the effort arm, how heavy of a person could be lifted who sat on the other end?
Given: Mechanical advantage = M.A. = 0.5, Effort = P = 600 N
To Find: Load = W =?
Solution:
M.A. = W/P
W = M.A. x P = 0.5 x 600 = 300 N
Ans: A person of weight 300 N can be lifted.
Example 07:
A force of 50 N is required to cut a metal sheet. A shears used for cutting the metal sheet has its blades 5 cm long, while its handle is 10 cm long. What effort is needed to cut the sheet?
Given: Load = W = 50 N, Effort arm = E.A. = 10 cm, Load arm = L.A. = 5 cm
To Find: Effort = P =?
Solution:
Mechanical advantage = Effort arm/Load arm
M.A. = 10 / 5 = 2
Now, M.A. = W/P
P = W/M.A. = 50/2 = 25 N
Ans: Effort needed to cut sheet is 25 N.
Example 08:
A crowbar 2 m long is pivoted about a point 10 cm from its tip. What is the least force which must be applied at the other end to displace a load of 1000 N.
Given: Load = W = 1000 N, Effort arm = E.A. = 2 m – 10 cm = 1.9 m, Load arm = L.A. = 10 cm = 0.1 m.
To Find: Effort = P =?
Solution:
Mechanical advantage = Effort arm/Load arm
M.A. = 1.9 / 0.1 = 19
Now, M.A. = W/P
P = W/M.A. = 1000/19 = 52.6 N
Ans: Effort = 52.6 N.
Example 09:
The diagram below shows a lever in use. (a) To which class of lever does it belong? (b) If AB =1 m, AF= 0.4 m, find its mechanical advantage. (c) Calculate the value of E.
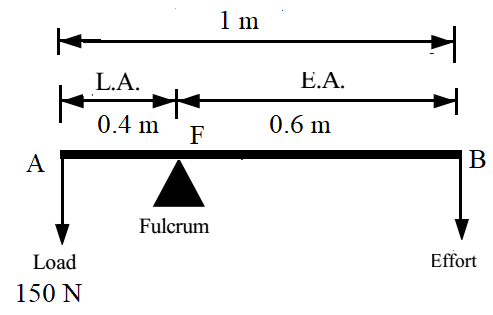
Solution:
The fulcrum lies between the effort and load, hence it is class I lever.
M.A. = E.A / L.A. = 0.6/0.4 = 1.5
M.A. = W/P
P = W/M.A. = 150/1.5 = 100 N
Ans: It is class I lever, mechanical advantage is 1.5, and effort required to lift 150 N load is 100 N.
Example 10:
The diagram below shows a lever in use. (a) To which class of lever does it belong? (b) If AB =1.2 m, AF= 0.2 m, find its mechanical advantage. (c) Calculate the value of E.
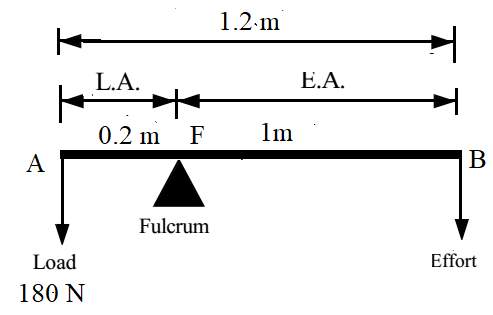
Solution:
The fulcrum lies between the effort and load, hence it is class I lever.
M.A. = E.A / L.A. = 1/0.2 = 5
M.A. = W/P
P = W/M.A. = 180/5 = 36 N
Ans: It is class I lever, mechanical advantage is 5, and effort required to lift 180 N load is 36 N.
Example 11:
A man uses a crowbar of length 1.5 m to raise a load of 750 N by putting a sharp edge below the bar at a distance 1 m from his hand. (a) Draw a diagram of the arrangement showing the fulcrum (F), load (L) and effort (E) with their directions. (b) State the kind of lever. (c) Calculate i) mechanical advantage and (ii) the effort needed.
Solution:

The fulcrum lies between the effort and load, hence it is class I lever.
M.A. = E.A / L.A. = 1/0.5 = 2
M.A. = W/P
P = W/M.A. = 750/2 = 375 N
Ans: It is class I lever, mechanical advantage is 2, and effort required to lift 750 N load is 375 N.
Example 12:
A pair of scissors is used to cut a piece of a cloth by keeping it at a distance 8.0 cm from its rivet and applying an effort of 100 N by fingers at a distance 2.0 cm from the rivet. (a) Find: (i) the mechanical advantage of scissors and (ii) the load offered by the cloth. (b) How does the pair of scissors act: as a force multiplier or as a speed multiplier?
Given: Load arm = L.A. = 8.0, Effort arm = E.A. 2.0 cm, Effort = P = 100 N,
To Find: Mechanical advantage = M.A. =?, Load = W = ?
Solution:
M.A. = E.A / L.A. = 2.0/8.0 = 0.25
M.A. = W/P
W = P x M.A. = 100 x 0.25 = 25 N
As M.A. < 1 scissor is acting as speed multiplier
Ans: Mechanical advantage is 0.25, and load offered by cloth is 25 N. The scissor is acting as speed multiplier.
Example 13:
A lever of length 9 cm has its load arm 5 cm long and the effort arm is 9 cm long. (a) To which class does it belong? (b) Draw diagram of the lever showing the position of fulcrum F and directions of both the load L and effort E. (c) What is the mechanical advantage and velocity ratio if the efficiency is 100%? (d) What will be the mechanical advantage and velocity ratio if the efficiency becomes 50%?
Given: Load arm = L.A. = 5cm, Effort arm = E.A. = 9 cm,
To Find: M.A. =? V.R. =? When Efficiency = 100 %, M.A. =? V.R. =? When Efficiency = 50 %
Solution:
In this case, effort arm is equal to lever length and it is also more than the load arm. it means load is between fulcrum and effort. It is class II lever.

M.A. = E.A./L.A. = 9/5 = 1.8
Efficiency = (M.A/V.R.) x 100
V.R. = (M.A. x 100)/Efficiency
When efficiency is 100%
V.R. = (1.8. x 100)/100 = 1.8
When efficiency is 50%
V.R. remains the same, M.A. decreases
M.A.. = (Efficiency x V.R.)/100
M.A. = (50 x 1.8)/100 = 0.9
Ans: When efficiency is 100 %, M.A. = 1.8 and V.R. = 1.8
When efficiency is 50 %, M.A. = 0.9 and V.R. = 1.8
Example 14:
The diagram below shows a lever in use. (a) To which class of lever does it belong? (b) If FA = 80 cm, AB = 20 cm, find its mechanical advantage. (c) Calculate the value of E

Solution:
In this case, the effort is between the fulcrum and the load, it is class III lever.
L.A. = 80 + 20 = 100 cm
M.A. = E.A./L.A. = 80/100 = 0.8
M.A. = W/P
P = W/M.A. = 50/0.8 = 62.5 N
Ans: It is a class III lever, M.A. = 0.8, Effort = 62.5 N
Example 14:
The diagram below shows a lever in use. (a) To which class of lever does it belong? (b) If FA = 80 cm, AB = 20 cm, find its mechanical advantage. (c) Calculate the value of E if load is 50 N

In this case, the load is between the fulcrum and the effort, it is class II lever.
E.A. = FA + AB = 80 + 20 = 100 cm
M.A. = E.A./L.A. = 100/80 = 1.25
M.A. = W/P
P = W/M.A. = 50/1.25 = 40 N
Ans: It is a class II lever, M.A. = 1.25, Effort = 40 N
One reply on “Numerical Problems on Levers”
It is really helpful to me, thanks alot