Numerical Problems on Newton’s Law of Cooling

Science > Physics > Radiation > Numerical Problems on Newton’s Law of Cooling

In this article, we are going to study to solve numerical problems based on Newton’s law of cooling.

Newton’s Law of Cooling:

The rate of loss of heat by a body is directly proportional to its excess temperature over that of the surroundings provided that this excess is small.

Let θ and θ_o, be the temperature of a body and its surroundings respectively. Let dQ / dt be the rate of loss of heat, So from Newton’s Law of Cooling,

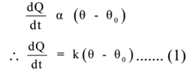
Where k is a constant. Sometimes constant is denoted by C

Example – 01:

A metal sphere, when suspended in a constant temperature enclosure, cools from 80 °C to 70 °C in 5 minutes and to 62^oC in the next five minutes. Calculate the temperature of the enclosure.

Solution:

Let θ_o be the temperature of the surroundings.

Consider a cooling from 80 °C to 70 °C:

Initial temperature = θ₁ = 80 °C, Final temperature = θ₂ = 70 °C, Time taken t = 5 min

By Newton’s Law of Cooling

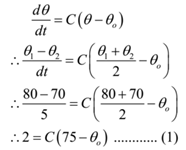
Consider a cooling from 70 °C to 62°C:

Initial temperature = θ₁ = 70 °C, Final temperature = θ₂ = 62 °C, Time taken t = 5 min

Dividing equation (1) by (2)

132 – 2 θ_o = 120 – 1.6θ_o

12 = 0.4 θ_o

θ_o = 12/0.4 = 30 °C

Ans: Surrounding temperature is 30 °C.

Example – 02:

A metal sphere cools at the rate of 3 °C per minute when its temperature is 50 °C. Find its rate of cooling at 40 °C if the temperature of the surroundings is 25 °C.

Solution:

Consider the cooling when the temperature was 50 °C:

Rate of cooling (dθ/dt)₁= 3 °C per minute, temperature of body = θ₁ = 50°C, temperature of surroundings = θ_o = 25 °C

Newton’s Law of Cooling

Consider the cooling when the temperature was 40 °C:

Temperature of body = θ₁ = 40 °C, temperature of surroundings = θ_o = 25 °C, Rate of cooling (dθ/dt)₂= ?

Ans: The rate of cooling at 40 °C is 1.8 °C per minute,

Example – 03:

A body cools at the rate of 0.5 °C/s when it is 500C above the surroundings. What is the rate of cooling when it is at 30 °C above the same surroundings?

Solution:

Consider the cooling when the temperature is 50 °C above the surroundings:

Rate of cooling (dθ/dt)₁= 0.5 °C per second, the temperature of the body above surroundings = (θ₁ – θ_o)= 50 °C,

By Newton’s law of cooling

Consider the cooling when the temperature is 30 °C above the surroundings:

Temperature of the body above surroundings = (θ₁ – θ_o)= 30 °C, Rate of cooling (dθ/dt)₂= ?

Ans: The rate of cooling at 30 °C above the  surroundings is1.8 °C per minute,

Example – 04:

A metal sphere cools at the rate of 0.6 °C per minute when its temperature is 30 °C above the surroundings. At what rate will it cool when its temperature is 20 °C above surroundings, other conditions remaining constant?

Solution:

Consider the cooling when the temperature is 30 °C above the surroundings:

Rate of cooling (dθ/dt)₁= 0.6 °C per minute, the temperature of the body above surroundings = (θ₁ – θ_o)= 30 °C,

By Newton’s Law of Cooling

Consider the cooling when the temperature is 20 °C above the surroundings:

Temperature of the body above surroundings = (θ₁ – θ_o)= 20 °C,

Rate of cooling (dθ/dt)₂= ?

Ans: The rate of cooling at 20 °C above the  surroundings is 0.4 °C per minute,

Example – 05:

A body at 50 °C cools in surroundings at 30 °C. At what temperature will its rate of cooling be half that at the beginning?

Solution:

Temperature of surroundings = θ_o = 30 °C

Consider the cooling when the temperature was θ₁= 50 °C

By Newton’s Law of Cooling

Consider the cooling when the temperature was θ₁ °C:

Rate of cooling (dθ/dt)₂= ½ (dθ/dt)₁

Ans: at 40 °C the rate of cooling be half that at the beginning

Example – 06:

A body cools from 75 °C to 55 °C in ten minutes when the surrounding temperature is 31°C. At what average temperature will its rate of cooling be ¼ th that at the start?

Solution:

Let θ_o be the temperature of the surroundings.

Consider a cooling from 75 °C to 55 °C :

Initial temperature = θ₁ = 75 °C, Final temperature = θ₂ = 55 °C, Time taken t = 10 min

Consider the cooling when the temperature was θ₁ °C:

Rate of cooling (dθ/dt)₂= 1/4 (dθ/dt)₁

Ans: At temperature 39.5 °C the rate of cooling be ¼ th that at the start

Example – 07:

A body cools from 60 °C to 50 °C in 5 minutes. How much time will it take to cool from 50 °C to 44 °C if the surrounding temperature is 32 °C?

Solution:

Let θ_o = 44 °C  be the temperature of surroundings.

Consider a cooling from 60 °C to 50 °C :

Initial temperature = θ₁ = 60 °C, Final temperature = θ₂ = 50 °C, Time taken t = 5 min

By Newton’s law of cooling

Consider a cooling from 50 °C to 44 °C :

Initial temperature = θ₁ = 50 °C, Final temperature = θ₂ = 44 °C

Ans: Time taken to cool from 50 °C to 44 °C is 4.6 min

Example – 08:

A body cools from 72 °C to 60 °C in 10 minutes. How much time will it take to cool from 60 °C to 52 °C if the temperature of the surroundings is 36 °C?

Solution:

Surrounding temperature = θ_o = 36 °C

Consider a cooling from 72 °C to 60 °C:

Initial temperature = θ₁ = 72 °C, Final temperature = θ₂ = 60 °C, Time taken t = 10 min

By Newton’s law of cooling

Consider a cooling from 60 °C to 52 °C :

Initial temperature = θ₁ = 60 °C, Final temperature = θ₂ = 52 °C

Ans: The time taken to cool from 60 °C to 52 °C is 10 min

Example – 09:

A body cools from 750C to 70 °C in 2 minutes. What will additional time it take to cool to 60 °C if the room temperature is 30 °C?

Solution:

Surrounding temperature = θ_o = 30 °C

Consider a cooling from 75 °C to 70 °C :

Initial temperature = θ₁ = 75 °C, Final temperature = θ₂ = 70 °C, Time taken t = 2 min

Consider a cooling from 70 °C to 60 °C :

Initial temperature = θ₁ = 70 °C, Final temperature = θ₂ = 60 °C

Ans: The time taken to cool from 70 °C to 60 °C is 34/7 min

Example – 10:

A heated metal ball is placed in cooler surroundings. Its rate of cooling is 2 °C per minute when its temperature is 60 °C and 1.2 °C per minute when its temperature is 52 °C. Find the temperature of the surroundings and the rate of cooling when the temperature of the ball is 48 °C.

Solution:

Let θ_o be the temperature of the surroundings.

Consider a cooling at 60 °C:

Temperature = θ₁ = 60 °C, Rate of cooling = 2 °C per minute

Consider a cooling at 52 °C:

Temperature = θ₂ = 52 °C, Rate of cooling = 1.2 °C per minute

Dividing equation (1) by (2)

∴   52 – θ_o = 36 – 0.6 θ_o

∴   16 = 0.4 θ_o

∴   θ_o = 40 °C

substituting in equation (1)

2 = C (60 – 40)

∴   C = 1/10 min^-1

Consider a cooling at 48 °C:

Temperature = θ₃ = 48 °C,

Ans: Temperature of surrounding is 40 °C and rate of cooling at 48 °C is 0.8 °C per min

Example – 11:

A copper ball cools from 62 °C to 50 °C in 10 minutes and to 42 °C in the next 10 minutes. Calculate the temperature at the end of next 10 minutes.

Solution:

Let θ_o be the temperature of the surroundings.

Consider a cooling from 62 °C to 50 °C:

Initial temperature = θ₁ = 62 °C, Final temperature = θ₂ = 50 °C, Time taken t = 10 min

By Newton’s law of cooling

Consider a cooling from 50 °C to 42 °C:

Initial temperature = θ₁ = 50 °C, Final temperature = θ₂ = 42 °C, Time taken t = 10 min

Dividing equation (2) by (1)

∴    138 – 3θ_o = 112 – 2θ_o

∴   θ_o  =26 ^oC

Surrounding temperature is 26 ^oC

substituting in equation (1)

1.2 = C( 56 -26)

∴    C = 1.2/30 = 1/25 min^-1

Consider further cooling from 42 ^oC to θ₂ ^oC:

Initial temperature = θ₁ = 50 ^oC, Final temperature = θ₂, Time taken t = 10 min

Ans: Temperature after next 10 minutes is 36.7 ^oC

Example – 12:

A body cools from 60 ^oC to 52 ^oC in 5 minutes and from 52 ^oC to 44 ^oC in next 7.5 minutes. Determine its temperature in the next 10 minutes.

Solution:

Let θ_o be the temperature of the surroundings.

Consider a cooling from 60 ^oC to 52 ^oC :

temperature = θ₁ = 60 ^oC, Final temperature = θ₂ = 52 ^oC, Time taken t = 5 min

By Newton’s law of cooling

Consider a cooling from 52 ^oC to 44 ^oC :

Initial temperature = θ₁ = 52 ^oC, Final temperature = θ₂ = 42 ^oC, Time taken t = 7.5 min

Dividing equation (2) by (1)

∴    72 – 1.5 θ_o = 56 – θ_o

∴    16 = 0.5 θ_o

∴    θ_o = 16/0.5 = 32 ^oC

Surrounding temperature is 32 ^oC

substituting in equation (1)

1.6 = C( 56 -32)

C = 1.6/24 = 1/15 min^-1.

Consider further cooling from 44 ^oC to θ₂ ^oC :

Initial temperature = θ₁ = 44 ^oC, Final temperature = θ₂, Time taken t = 10 min

Ans: The temperature after 10 minutes is 38 ^oC

Examples – 13:

A body cools from 60 ^oC to 52 ^oC in 10 minutes and to 46 ^oC in the next 10 minutes. Find the temperature of the surroundings.

Solution:

Let θ_o be the temperature of surroundings.

Consider a cooling from 60 ^oC to 52 ^oC :

Initial temperature = θ₁ = 60 ^oC, Final temperature = θ₂ = 52 ^oC, Time taken t = 10 min

By Newton’s law of cooling

Consider a cooling from 52 ^oC to 46 ^oC :

Initial temperature = θ₁ = 52 ^oC, Final temperature = θ₂ = 46 ^oC, Time taken t = 10 min

Dividing equation (2) by (1)

∴    196 – 4θ_o = 168 – 3θ_o

∴     θ_o = 28

Ans: Surrounding temperature is 28 ^oC

Example – 14:

The rate of cooling of a body is 2 ^oC/min at temperature 60 ^oC and 1 ^oC/min at 45 ^oC. What will be the temperature of the surroundings?

Solution:

Let θ_o be the temperature of the surroundings.

Consider the cooling when temperature θ₁ = 60 ^oC:

Rate of cooling (dθ/dt)₁= 2 ^oC per minute,

By Newton’s law of cooling

Consider the cooling when temperature θ₂ = 30 ^oC:

Rate of cooling (dθ/dt)₁= 1 ^oC per minute,

Dividing equation (1) by (2)

∴  90 – 2θ_o= 60 – θ_o

∴  θ_o = 30 ^oC

Ans: Surrounding temperature is 30^oC

Example – 15: 

A metal sphere cools from 60 ^oC to 50 ^oC in 5 minutes. How much more time will it take to cool from 50 ^oC to 40 ^oC if the temperature of the surroundings is 30 ^oC.

Solution:

Let θ_o be the temperature of surroundings.

Consider a cooling from 60 ^oC to 50 ^oC :

Initial temperature = θ₁ = 60 ^oC, Final temperature = θ₂ = 50 ^oC, Time taken t = 5 min

By Newton’s law of cooling

Consider a cooling from 50 ^oC to 40 ^oC :

Initial temperature = θ₁ = 50 ^oC, Final temperature = θ₂ = 40 ^oC, Time taken t = ?

Ans: Time taken to cool from 50 ^oC to 40 ^oC is 8.33 min

Example – 16:

A copper sphere is heated and then allowed to cool while suspended in an enclosure whose walls are maintained at a constant temperature. When the temperature of the sphere is 86 ^oC, it is cooling at the rate of 3 ^oC/min; at 75 ^oC, it is cooling at the rate of 2.5 ^oC/min. What is the temperature of the sphere when it is cooling at the rate of 1 ^oC/min? Assume Newton’s law of cooling.

Solution:

Let θ_o be the temperature of surroundings.

Consider the cooling when temperature θ₁ = 86 ^oC:

Rate of cooling (dθ/dt)₁= 3 ^oC per minute,

By Newton’s law of cooling

Consider the cooling when temperature θ₁ = 75 ^oC:

Rate of cooling (dθ/dt)₁= 2.5 ^oC per minute,

Dividing equation (2) by (1)

∴  450 – 6θ_o = 430 – 5 θ_o

∴  θ_o = 20 ^oC

Substituting in equation (1)

3 = C(86 – 20)

∴   C = 3/66 = 1/22 min^-1

Consider the cooling when temperature = θ₃:

Rate of cooling (dq/dt)₁=  1 ^oC per minute,

Ans: At 42 ^oC it is cooling at the rate of 1 ^oC/min

Previous Topic: Stefan’s Law of Rdaiation

Click Here for More Topics in Physics

Science > Physics > Radiation > Numerical Problems on Newton’s Law of Cooling