Science > Physics > Motion in a Straight Line > Numerical Problems on Uniformly Accelerated Bodies Set – 02
In this article we shall study to solve more problems on uniformly accelerated bodies.
Example 01:
The initial velocity of a car is 10 ms-1. It accelerates uniformly at 2 ms-2 for 20 s and thereafter retards uniformly at 4 ms-2. Find the total distance covered by the car before it comes to rest. For how much time the car is in motion?
To Find: Total distance covered = AB =? Total time = t =?
Solution:
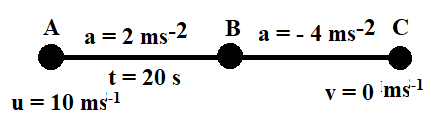
Consider motion of the body between A and B
At point A, Initial velocity u = 10 ms-1, Acceleration = a = 2 ms-2, Time taken = t = 20 s.
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (10)(20) + ½ (2)(20)2
∴ s = 200 + 400
∴ s = 600 m
∴ AB = 600 m
By Newton’s first equation of motion
v = u + at
v = 10 + (2)(20)
v = 10 + 40
v = 50 ms-1
Consider motion of the body between B and C
At point A, Initial velocity u = 50 ms-1, Acceleration = a = – 4 ms-2, Final velocity = v = 0 ms-1.
By Newton’s third equation of motion
v2 = u2 + 2as
∴ 02 = 502 + 2(-4)s
∴ 0 = 2500 – 8s
∴ 8 s = 2500
∴ s = 2500/8 = 312.5 m
∴ BC = 312.5 m
By Newton’s first equation of motion
v = u + at
∴ 0 = 50 + (-4) t
∴ 4t = 50
∴ t = 50/4 = 12.5 s
∴ Total distance covered = 600 + 312.5 = 912.5 m
∴ Total time taken = 20 + 12.5 = 32.5 s
Ans: Total distance travelled by car is 912.5 m and total time taken is 32.5 s
Example 02:
The initial velocity of car is 5 ms-1. It accelerates uniformly at 0.5 ms-2 for 30 s and then retards uniformly at 2 ms-2. Find the distance covered by the car before it comes to rest. For how much time is the car is in motion?
To Find: least time in which body can complete a journey of 5 km =?
Solution:
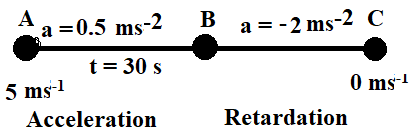
Consider motion of body from A to B.
Initial velocity = u = 5 ms-1, Acceleration = a = 0.5 ms-2, Time taken = t = 30 s
By Newton’s first equation of motion
v = u + at
∴ v = 5 + (0.5) x 30
∴ v = 5 + 15 = 20 ms-1
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (5)(30) + ½ (0.5) (30)2
∴ s = 150 + ½ (0.5) (900)
∴ s = 150 + 225 = 375 m
∴ s = AB = 375 m
Consider motion of body from B to C.
By Newton’s first equation of motion
v = u + at
∴ 0 = 20 + (- 2) t
∴ – 20 = – 2 t
∴ t = 20/2 = 10 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (20)(10) + ½ (-2) (10)2
∴ s =200 – 100 = 100 m
∴ BC = 100 m
Total Distance travelled = AC
∴ AC = AB + BC = 375 + 100 = 475 m
Total time taken = t = tAB + tBC + tCD
∴ t = 30 + 10 = 40 s
Ans: The distance covered by the car before it comes to rest is 475 m and the car is in motion for 40 s.
Note: V. T. Diagram for motion is
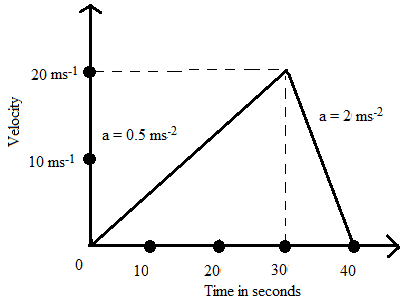
Example 03:
A body starting from rest accelerates uniformly at 0.1 ms-2 and retards uniformly at 0.2 ms-2. What is the least time in which it can complete a journey of 5 km if it attains a maximum velocity of 72 km h-1.
To Find: least time in which body can complete a journey of 5 km =?
Solution:

Consider motion of body from A to B.
Initial velocity = u = 0 ms-1, Final velocity = 72 km h-1 = 72 x (5/18) = 20 ms-1, Acceleration = a = 0.1 ms-2,
By Newton’s first equation of motion
v = u + at
∴ 20 = 0 + (0.1) t
∴ 20 = 0. 1 t
∴ t = 20/0.1 = 200 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(200) + ½ (0.1) (200)2
∴ s = ½ (0.1) (40000)
∴ s = AB = 2000 m
Consider motion of body from C to D.
By Newton’s first equation of motion
v = u + at
∴ 0 = 20 + (- 0.2) t
∴ – 20 = – 0. 2 t
∴ t = 20/0.2 = 100 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (20)(100) + ½ (- 0.2) (100)2
∴ s =2000 – (0.1) (10000)
∴ s = 2000 – 1000 = 1000 m
∴ CD = 1000 m
Now AD = 5 km = 5000m
∴ AD = AB + BC + CD
∴ BC = AD – AB – CD = 5000 – 2000 – 1000 = 2000 m
To have a displacement of 5 km in minimum time, the body should cover distance between B and C (2000 m) with the maximum velocity attained (20 ms-1).
For uniform motion
s = vt
∴ t = s/v = 2000/20 = 100 s
Total time taken = t = tAB + tBC + tCD
∴ t = 200 + 1000 + 100 = 400 s
Ans: The journey of 5 km can be completed in the least time of 400 s.
Note:
V-T Diagram for the motion is

Example 04:
A body accelerates uniformly at 0.2 ms-2 and retards uniformly at 0.3 ms-2 If the maximum velocity attained by it is 30 ms-1, find the least time in which it can complete a journey of 6 km.
To Find: least time in which body can complete a journey of 6 km =?
Solution:

Consider motion of body from A to B.
Initial velocity = u = 0 ms-1, Final velocity = 30 ms-1, Acceleration = a = 0.2 ms-2,
By Newton’s first equation of motion
v = u + at
∴ 30 = 0 + (0.2) t
∴ 30 = 0. 2 t
∴ t = 30/0.2 = 150 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(150) + ½ (0.2) (150)2
∴ s = (0.1) (22500)
∴ s = AB = 2250 m
Consider motion of body from C to D.
By Newton’s first equation of motion
v = u + at
∴ 0 = 30 + (- 0.3) t
∴ – 30 = – 0. 3 t
∴ t = 30/0.3 = 100 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (30)(100) + ½ (- 0.3) (100)2
∴ s =3000 – ½ (0.3) (10000)
∴ s = 3000 – 1500 = 1500 m
∴ CD = 1500 m
Now AD = 6 km = 6000m
∴ AD = AB + BC + CD
∴ BC = AD – AB – CD = 6000 – 2250 – 1500 = 2250 m
To have a displacement of 6 km in minimum time, the body should cover distance between B and C (2250 m) with the maximum velocity attained (30 ms-1).
For uniform motion
s = vt
∴ t = s/v = 2250/30 = 75 s
Total time taken = t = tAB + tBC + tCD
∴ t = 150 + 75 + 100 = 325 s
Ans: The journey of 6 km can be completed in the least time of 325 s.
Note:
V-T Diagram for the motion is

Example 05:
Two cars P and Q start side by side from the same instant and in the same direction. P accelerates uniformly at 4 ms-2 for 10 seconds and then moves with uniform velocity. Q moves with a uniform acceleration of 3 ms-2. Find the distance between them 30 seconds after start.
Solution:
Consider motion of Car P.
Consider accelerated motion of Car P
Initial velocity = u = 0 ms-1, Acceleration = a = 4 ms-2, Time for acceleration = t = 10 s,
By Newton’s first equation of motion
v = u + at
∴ v = 0 + (4) (10)
∴ v = 40 ms-1
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(10) + ½ (4) (10)2
∴ s = 0 + 2 x 100 = 200 m
Consider uniform motion of car P
Uniform velocity = 40 ms-1, Time for uniform motion = t = 30 s – 10 s = 20 s.
S = ut = 40 x 20 = 800 m
∴ Total distance travelled by car P = 200 + 800 = 1000 m
Consider motion of car Q.
Consider accelerated motion of car Q
Initial velocity = u = 0 ms-1, Acceleration = a = 3 ms-2, Time for acceleration = t = 30 s,
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(30) + ½ (3) (30)2
∴ s = 0 + ½ (3) (900) = 1350 m
∴ Total distance travelled by car Q = 1350 m
Distance between the two cars = 1350 – 1000 = 350 m
Ans: Car Q is ahead of car P by 350 m
Example 06:
A car A is travelling along a straight level road with a uniform speed of 60 kmh-1. It is followed by another car B which is travelling uniformly at 70 kmh-1. When the distance between them is 2.5 km, the car B decelerates at 20 kmh-2 when will B catch up with A?
Solution:
Let us assume the car B catches car A after t hours
Distance travelled by car A during this period’
s = ut = 60 x t = 60 t km
Distance between the two cars is 2.5 km
Thus car B has to cover a distance of (60 t + 2.5) km to catch car A.
Distance travelled by car B during this period
s = ut + ½ at2
∴ s = 70 x t + ½ (- 20) t2
∴ s = 70 t – 10 t2
As car B is overtaking
∴ 60 t + 2.5 = 70 t – 10 t2
∴ 10 t2 – 10 t + 2.5 = 0
∴ 4 t2 – 4 t + 1 = 0
∴ (2t – 1)2 = 0
∴ 2t – 1 = 0
∴ t = ½ h = 30 min
Ans: Thus car B will catch car A after 30 min from the start of deceleration.
Example 07:
Starting from rest, a car P travels with a uniform acceleration of 2 ms-2 starting from rest from the same point 4s later, a car Q travels with an acceleration of 8 ms-2 in the same direction as P. Find the time required by Q to overtake P. What is the distance travelled by each car?
Solution:
Let us assume that the two cars meet after t second after the start of car P
Consider motion of car P
Initial velocity = u = 0 ms-1, Acceleration = a = 2 ms-2, Time = t s,
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(t) + ½ (2) (t)2
∴ s = t2 m
Consider the motion of car Q
Initial velocity = u = 0 ms-1, Acceleration = a = 8 ms-2, Time = (t – 4) s,
s = ut + ½ at2
∴ s = (0)(t – 4) + ½ (8) (t – 4)2
∴ s = 4(t2 – 8t + 16) m
∴ s = (4t2 – 32t + 64) m
As the car Q is over taking
Distance travelled by car Q = Distance travelled by car P
∴ 4t2 – 32t + 64 = t2
∴ 3t2 – 32t + 64 = 0
∴ 3t2 – 24t – 8 t + 64 = 0
∴ 3t(t – 8) – 8 (t – 8) = 0
∴ (t – 8) (3t – 8) = 0
∴ t – 8 = 0 or t3t – 8 = 0
∴ t = 8 s or t = 8/3 = 2.67 s
t = 3.67 s < 4 s hence not practicable
∴ t = 8 s
∴ Distance travelled by each car = t2 = 82 = 64 m
Ans: Car Q will overtake car P after 8 s, when car P starts moving and each car will cover a distance of 64 m.