Science > Physics > Motion in a Straight Line > Numerical Problems on Uniformly Accelerated Bodies Set – 03
Expression for the Distance Travelled by Body in nth Second of its Motion:
By Newton’s Second equation of motion, s = ut + ½ at²
where s = displacement of body in ‘t’ seconds
u = initial velocity of the body, a = acceleration of the body, t = time
The distance travelled by body in ‘n’ seconds is given by
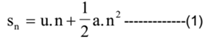
This distance by travelled by the body in (n-1) seconds is given by
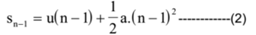
∴ The distance travelled by the body in n th second
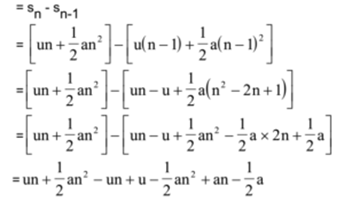

Example 01:
A body starts from rest and moves with uniform acceleration of 0.25 ms-2 find the distance travelled by it in 10 s and its velocity. Find also the distance covered by it in the 10th second of its motion.
Given: Acceleration = a = 0.25 ms-2, Initial velocity = u = 0 ms-1.
To Find: Distance travelled in 10 second =? Distance travelled in 10th second = s15 =?
Solution:
Distance travelled in 10 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (0)(10) + ½ (0.25)(10)2
∴ s = 0.125 x 100 = 12.5 m
Velocity at end of 10 s
By Newton’s first equation of motion
v = u + at
∴ v = 0 + 0.25 x 10 = 2.5 ms-1
Distance travelled in 10th second
Sn = u + ½ a (2n – 1)
∴ s10 = 0 + ½ (0.25) (2(10) – 1)
∴ s10 = 0.125 (19)
∴ s10 = 2.375 m
Ans: Distance travelled in 10 s is 12.5 m, the velocity at end of 10 s is 2.5 ms-1, and the distance travelled in 10th second of motion is 2.375 m
Example 02:
A body starting from rest, travels with uniform motion. It covers 13.5 m in the 5th second of its motion. Find its acceleration.
Given: Initial velocity of the body = u = 0 ms-1, Distance travelled in fifth second = s5 = 13.5 m.
To Find: Acceleration = a =?
Solution:
Distance travelled by body in nth second of its motion with uniform acceleration is given by
Sn = u + ½ a (2n – 1)
Distance travelled in 5th second of motion
S5 = 0 + ½ a (2(5) – 1) 13.5
∴ 9/2 a = 13.5
∴ a = 3 ms-2
Ans: Acceleration is 3 ms-2.
Example 03:
A body moving with uniform acceleration covers 15 m in the third second of its motion and 19.4 m in the fifth second. If its acceleration is uniform, find its acceleration and initial velocity.
Given: Distance travelled in third second = s3 = 15 m, Distance travelled in fifth second = s5 = 19.4 m
To Find: Acceleration = a =? Initial velocity = u =?
Solution:
Distance travelled by body in nth second of its motion with uniform acceleration is given by
Sn = u + ½ a (2n – 1)
Distance travelled in the third second of the journey
∴ S3 = u + ½ a (2(3) – 1) = 15
∴ u + 5/2 a = 15
∴ 2u + 5a = 30 ………… (1)
Distance travelled in the fifth second of the journey
∴ S5 = u + ½ a (2(5) – 1) = 19.4
∴ u + 9/2 a = 19.4
∴ 2u + 9a = 38.8 ………… (2)
Solving equation (1) and (2) simultaneously
u = 9.5 ms-1 and a = 2.2 ms-2
Ans: Acceleration is 2.2 ms-2 and velocity is 9.5 ms-1.
Example 04:
A particle covers 45 m in the 7th second and 75 m in the 12th second of its motion. Find the initial velocity and acceleration.
Given: Distance travelled in 7th second = s7 = 45 m, Distance travelled in 12th second = s12 = 75 m
To Find: Acceleration = a =? Initial velocity = u =?
Solution:
Distance travelled by body in nth second of its motion with uniform acceleration is given by
Sn = u + ½ a (2n – 1)
Distance travelled in the 7th second of the journey
∴ S7 = u + ½ a (2(7) – 1) = 45
∴ u + 13/2 a = 45
∴ 2u + 13a = 90 ………… (1)
Distance travelled in the 12th second of the journey
∴ S12 = u + ½ a (2(12) – 1) = 75
∴ u + 23/2 a = 75
∴ 2u + 23a = 150 ………… (2)
Solving equation (1) and (2) simultaneously
u = 6 ms-1 and a = 6 ms-2
Ans: velocity is 6 ms-1 and acceleration is 6 ms-2.
Example 05:
A body moving with uniform acceleration covers 65 cm in the 5th second and 105 cm in the 9th second. What distance does it travel in 15 s and 15th second?
Given: Distance travelled in 5th second = s5 = 65 cm, Distance travelled in 9th second = s9 = 105 cm
To Find: Distance travelled in 15 second =? Distance travelled in 15th second = s15 =?
Solution:
Distance travelled by body in nth second of its motion with uniform acceleration is given by
Sn = u + ½ a (2n – 1)
Distance travelled in the 5th second of the journey
∴ S5 = u + ½ a (2(5) – 1) = 65
∴ u + 9/2 a = 65
∴ 2u + 9a = 130 ………… (1)
Distance travelled in the 9th second of the journey
∴ S9 = u + ½ a (2(9) – 1) = 105
∴ u + 17/2 a = 105
∴ 2u + 17a = 210 ………… (2)
Solving equation (1) and (2) simultaneously
u = 20 cms-1 and a = 10 cms-2
Distance travelled in 15 s
By Newton’s second equation of motion
s = ut + ½ at2
∴ s = (20)(15) + ½ (10)(15)2
∴ s = 300 + 5 x 225
∴ s = 1425 cm
Distance travelled in 15th second
∴ s15 = 20 + ½ (10) (2(15) – 1)
∴ s15 = 20 + 5 (29)
∴ s15 = 20 + 145 = 165 cm
Ans: Distance travelled in 15 s is 1425 cm and the distance travelled in 15th second is 165 cm.
Example 06:
A body moving with the uniform acceleration covers 25 cm and 33 cm in the fifth and seventh second respectively. Find its velocity at the end of 9th second from start.
Given: Distance travelled in fifth second = s5 = 25 cm, Distance travelled in seventh second = s7 = 33 cm
To Find: Velocity at end of 9th second =?
Solution:
Distance travelled by body in nth second of its motion with uniform acceleration is given by
Sn = u + ½ a (2n – 1)
Distance travelled in the fifth second of the journey
∴ S5 = u + ½ a (2(5) – 1) = 25
∴ u + 9/2 a = 25
∴ 2u + 9a = 50 ………… (1)
Distance travelled in the seventh second of the journey
∴ S9 = u + ½ a (2(7) – 1) = 33
∴ u + 13/2 a = 33
∴ 2u + 13a = 66 ………… (2)
Solving equation (1) and (2) simultaneously
u = 7 cms-1 and a = 4 cms-2
By Newton’s first equation of motion
v = u + at
∴ v = 7 + (4)(9) = 7 + 36 = 43 cms-1
Ans: The velocity at end of 9th second is 43 cms-1.