Science > Physics > Motion in a Straight Line > Numerical Problems on Uniformly Accelerated Bodies Set – 04
Important Formulae
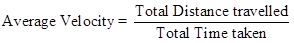
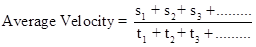


Example – 01:
A body rises vertically upward to a height of 100 m, in 5 seconds, then comes back at the same position after another 5 s. Find the average speed and average velocity of the body.
Given: Upward distance travelled = s1 = 100 m, time taken for upward journey = t1 = 5 s
Solution:
Distance travelled in downward journey = s2 = Distance travelled in upward journey = 100m
Time taken for downward journey = t2 = Time taken for downward journey = 5 s
Average Speed = Total distance travelled / Total time taken

vavg = 20 ms-1
As displacement is zero, velocity is also zero
Ans: The average speed is 20 ms-1 and average velocity is zero.
Example – 02:
A man covers a distance from a point P to a point Q in a straight line at a speed of 4 ms-1 and returns back along the same path at a speed of 8 ms-1. What is his average speed? What is his average velocity?
Solution:
Let ‘s’ be the distance between points P and Q.
Distance travelled in one direction = s1 = s.
Distance travelled in other direction = s2 = s.
Velocity in one direction = v1 = 4 ms-1
Velocity in other direction = v2 = 8 ms-1
Average Speed = Total distance travelled / Total time taken

Ans: Average speed is 5.33 m s-1
Example – 03:
A body travels from a point P to point Q by the shortest route with a velocity of 50 km h-1 and returns to P by the same route with a velocity of 70 km h-1. What is its average speed?
Solution:
Let ‘s’ be the distance between points P and Q.
Distance travelled in one direction = s1 = s.
Distance travelled in other direction = s2 = s.
Velocity in one direction = v1 = 50 km h-1
Velocity in other direction = v2 = 70 km h-1

Ans: Average speed is 58.33 km h-1
Example 04:
A car travels from A to B at a speed of 30 km h-1 and back to A at a speed of 40 km h-1. Find its average speed for the journey.
Solution:
Let ‘s’ be the distance between points A and B.
Distance travelled in one direction = s1 = s.
Distance travelled in other direction = s2 = s.
Velocity in one direction = v1 = 30 km h-1
Velocity in other direction = v2 = 40 km h-1

Ans: Average speed is 34.29 km h-1
Example 05:
A vehicle covers the first half of the distance between the two points with a speed of 40 km h-1 and the second half with a speed of 60 km h-1. Find its average speed?
Solution:
Let ‘s’ be the total distance.
Distance travelled in first part = s1 = s/2.
Distance travelled in second part = s2 = s/2.
Velocity in one direction = v1 = 40 km h-1
Velocity in other direction = v2 = 60 km h-1

Ans: Average speed is 48 km h-1
Example 06:
A car travels first 30 km at a uniform speed of 30 km h-1 and next 30 km at a uniform speed of 60 km h-1. Calculate the average speed of the car.
Solution:
Distance travelled in first part = s1 = 30 km.
Distance travelled in second part = s2 = 30 km.
Velocity in one direction = v1 = 30 km h-1
Velocity in other direction = v2 = 60 km h-1

Ans: Average speed is 40 km h-1
Example 07:
A car travels first 50 km at a uniform speed of 25 km h-1 and next 60 km at a uniform speed of 20 km h-1. Calculate the average speed of the car.
Solution:
Distance travelled in first part = s1 = 50 km.
Distance travelled in second part = s2 = 60 km.
Velocity in one direction = v1 = 25 km h-1
Velocity in other direction = v2 = 20 km h-1

Ans: Average speed is 22 km h-1
Example 08:
A car travels at a uniform speed of 30 km h-1 for 30 minutes and then at a uniform speed of 40 km h-1 for the next 40 min. Calculate the total distance travelled by car and its average speed.
Given: Speed for the first part of journey = v1 = 30 km h-1, time for first part of journey = t1 = 30 min = 30/60 = 1/2 h, Speed for the second part of journey = v2 = 40 km h-1, time for first part of journey = t2 = 40 min = 40/60 = 2/3 h,
To Find: Total distance travelled =? and average speed =?
Solution:
Total distance travelled = v1 t1 + v2 t2
Total distance travelled = 30 x (1/2) + 40 x (2/3)
Total distance travelled = 15 + 80/3 = 125/3
Total distance travelled = 41.67 km

Ans: Total distance travelled = 41.67 km and average speed = 35.71 km h-1
Example – 09:
A car travels at a uniform speed of 30 km h-1 for 30 minutes and then at a uniform speed of 60 km h-1 for next 30 min. calculate the average speed of the car.
Given: Speed for the first part of journey = v1 = 30 km h-1, time for first part of journey = t1 = 30 min = 30/60 = 1/2 h, Speed for the second part of journey = v2 = 60 km h-1, time for first part of journey = t2 = 30 min = 30/60 = 1/2 h,
To Find: average speed =?
Solution:
Total distance travelled = v1 t1 + v2 t2
Total distance travelled = 30 x (1/2) + 60 x (1/2)
Total distance travelled = 15 + 30 = 45 km

Example – 10:
A car is fitted with a speedometer which also gives reading of distance travelled by the car. At the start of the trio reading was found to be 1272 km and after 50 minutes at end of the trip is 1352 km. Calculate the average speed of the car.
Given: Initial reading = s1 = 1272 km, Final reading = s2 = 1352 km, time taken = 50 min = 50/60 = 5/6 h
To Find: average speed =?
Solution:
Total distance travelled = s2 – s1 = 1352 – 1272 = 80 km
Average speed = Total distance travelled / Total time taken
∴ Average speed = 80/( 5/6)= 96 km h-1
Ans: The average speed of car is 96 km h-1
Example – 11:
A train takes 2 h to reach from station A to station B which is at a distance of 200 km from station A. It takes 3 h for the return journey. What is the average speed and average velocity of the train?
Given: Distance travelled in first part of journey = s1 = 200 km, time taken for the first part of journey = t1 = 2 h, Distance travelled in second part of journey = s2 = 200 km, time taken for the second part of journey = t2 = 3 h.
To Find: average speed =?
Solution:
Average speed = Total distance travelled / Total time taken
Average speed = (s1 + s2)/(t1 + t2)
∴ Average speed = (200 + 200) / (2 + 3)
∴ Average speed = 400/5 = 80 km h-1
As the train is coming back to starting point its displacement is zero.
Hence its average velocity = 0
Ans: The average speed = 80 km h-1 and average velocity = 0
Example 12:
A body travels straight along a level road. For the first half-time, its speed its speed is v1 and for the second half-time, its speed is v2. What is its average speed? What would the average speed be if the first half-distance is covered with speed v1 and the second half-distance is covered with speed v2?
Solution:
Part – I:
Let t be the time taken by the body to complete the journey.
Let distance travelled by the body with velocity v1 in time t1 (= t/2) be s1. Let distance travelled by the body with velocity v2 in time t2 (= t/2) be s2.

Part – II:
Let s be the total distance travelled by the body.
Let distance travelled by the body with velocity v1 be s1 (= s/2).
Let distance travelled by the body with velocity v2 be s2 (= s/2).

Example 13:
A particle describes a distance s in time t s when moving along a straight path with uniform acceleration a. If the in the next covers a distance s’, find expression for the acceleration of the particle.
Consider first part of the motion:
Distance travelled in t s is given by
s = ut + ½ at2 …………. (1)
Velocity at end of t s is
v = u + at
This velocity is initial velocity for the second part of motion
s’ = (u + at)t’ + ½ at’2
∴ s’ = u t’ + at t’ + ½ at’2 …………. (2)
Multiplying equation (1) by t’
∴ s t’ = utt’ + ½ a t’t2 …………. (3)
Multiplying equation (2) by t
s’t = utt’ + at2t’ + ½ att’2 …………. (4)
Subtracting equation (3) from (4)
∴ s’t – s t’ = utt’ + at2t’ + ½ att’2 – utt’ – ½ a t’t2
∴ s’t – s t’ = ½ att’2 + ½ a t’t2
∴ s’t – s t’ = ½ att’(t + t’)
∴ 2(s’t – s t’) = att’(t + t’)
∴ a = 2(s’t – s t’)/ tt’(t + t’)

Example 14:
A body with uniform acceleration has velocities of 20 m/s and 30 m/s when passing points P and Q in its path. Find its velocity at the point midway between P and Q.
Solution:

Let a be the acceleration and s be the total displacement of the body. Let us consider motion of the body from P to Q.
By Newton’s third equation of motion.
v2 = u2 + 2as
∴ 302 = 202 + 2as
∴ 900 – 400 = 2as
∴ 2as = 500
∴ as = 250 ……. (1)
Let R be the midpoint of the path. Let us consider motion of the body from P to R.
By Newton’s third equation of motion.
v2 = u2 + 2as
∴ v2 = 202 + 2a(s/2)
∴ v2 = 400 + as
∴ v2 = 400 + 250
∴ v2 = 650
∴ v = 25.49 ms-1
Ans: The velocity at point midway between P and Q is 25.49 ms-1.
Example 15:
A body moving with uniform acceleration has velocities of 30 m/s and 40 m/s when passing two points P and Q in its path. What is its velocity at the point mid-way between P and Q?
Solution:

Let a be the acceleration and s be the total displacement of the body. Let us consider motion of the body from P to Q.
By Newton’s third equation of motion.
v2 = u2 + 2as
∴ 402 = 302 + 2as
∴ 1600 – 900 = 2as
∴ 2as = 700
∴ as = 350 ……. (1)
Let R be the midpoint of the path. Let us consider motion of the body from P to R.
By Newton’s third equation of motion.
v2 = u2 + 2as
∴ v2 = 302 + 2a(s/2)
∴ v2 = 900 + as
∴ v2 = 900 + 350
∴ v2 = 1250
∴ v = 35.35 ms-1
Ans: The velocity at point midway between P and Q is 35.35 ms-1.
Example 16:
A train moving with uniform acceleration has its front end passing a given fixed point P with a speed of u and the tail end passing the same point P with a speed of v. What is the speed of the mid-point of the train when passing the point?
Solution:
Let a be the acceleration and s be the total displacement of the body. Let v’ be is velocity at the midpoint of train passing through point.
Consider motion for the first half.
By Newton’s third equation of motion.
v2 = u2 + 2as
∴ v’2 = u2 + 2a(s/2)
∴ v’2 = u2 + as ……. (1)
Consider motion for the second half.
By Newton’s third equation of motion.
v2 = v’2 + 2as
∴ v2 = v’2 + 2a(s/2)
∴ v2 = v’2 + as
∴ as = v2 – v’2
Substituting this value in equation (1)
v’2 = u2 + v2 – v’2 2v’2 = u2 + v2

Example 17:
C is a point midway between A and B. The average speed of a person from A to C is V. At what speed must he travel the remaining distance to have an average speed of 4v/3 for the whole journey?
Solution:
Let us assume that he travels the first half with velocity v1 (= v) and second half with speed v2

Ans: The person must travel remaining distance at an average speed of 2v.