Science > Physics > Oscillations: Simple Harmonic Motion > Introduction
In this article, we shall study the concept, oscillation, oscillatory motion, and simple harmonic motion.
Oscillatory Motion:
A to and fro periodic motion of a body along a definite path is called oscillatory motion. e.g. the motion of heavy bob of a pendulum, the motion of molecules of solid due to thermal energy.
Equilibrium concept in oscillation is very important because it is the basis of the oscillatory motion. If a system is disturbed from its equilibrium position and then left to itself, it starts oscillating about the equilibrium position which becomes the mean position of the oscillation.
Oscillation:
It is defined as a complete to and fro motion of a body performing oscillatory motion along its path. The body covers its path twice in one oscillation.
Examples of Oscillatory Motion:
- The motion of the heavy bob of the pendulum.
- The motion of pivoted magnetic needle in the uniform magnetic field.
- The Motion of molecules of solid due to thermal energy.
- The motion of the needle of a sewing machine.
- The motion of prongs of tuning fork.
- The motion of medium particles, when a longitudinal or transverse wave travels through it.
Harmonic Oscillation:
Harmonic oscillation is that motion which can be expressed in terms of a single harmonic function (sine or cosine function).
The displacement of a particle performing harmonic motion is given by
x = a sin (2πt/T) or x = a cos (2πt/T)
Non-Harmonic Oscillation:
Non-harmonic oscillation is that oscillation which cannot be represented by a single harmonic function.
Non-harmonic motion can be expressed mathematically as the sum of a number of harmonic motion.
x = a sin (2πt/T) + x = a sin (4πt/T) + x = a sin (6πt/T) + …..
Periodic Motion:
When the body performs the same set of movements again and again within a fixed interval of time, then the body is said to have periodic motion. e.g. the motion of the moon around the earth, the motion of the minute hand of a clock.
Oscillatory motion is always periodic motion. But every periodic motion need not be an oscillatory motion. For e.g. the motion of bob of an oscillating simple pendulum is an oscillatory motion as well as periodic motion, while the motion of the earth around the sun is a periodic motion but not oscillatory motion.
Extreme Position:
It is defined as the position of the body at which the body comes to rest momentarily. They are ends of the path and the body never moves beyond these positions.
Mean Position:
It is defined as the position of the body at which the net force acting on the body is zero. Hence this position is also called an equilibrium position. It is the centre of the path and the body moves equally on its two sides.
Displacement:
It is defined as the distance of the body from the mean position at that instant irrespective of the position from which it starts.
Periodic Function:
Any function which repeats after fixed (regular) intervals of time is called the periodic function.
Examples: The sine and cosine functions with fixed time period and frequency. f(t) = a sin (2πt/T) or f(t) = a cos (2πt/T)
If T is time period, then f (t + T) = f(t). Thus f(t) repeats after the time interval T. In general, periodic function can be represented as
f(t) = a sin (2πnt/T), where n = 1, 2, 3, 4, ……..
g(t) = a sin (2πnt/T), where n = 0, 1, 2, 3, ……..
Fourier Theorem:
Any periodic function F(t) of the time period T, however complex it may be, can be represented by a unique combination of the functions fn(t) and gn(t).
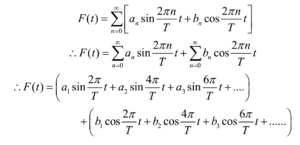
a1, a2, a3, …. and b1, b2, b3, …. are called Fourier coefficients. The values of a1, a2, a3, …. and b1, b2, b3, …. depend on the nature of the periodic function. If a1 ≠ 0 and b1 ≠ 0 and all other Fourier coefficients are zero then the Fourier equation represents a special case of periodic motion called simple harmonic motion.
Simple Harmonic Motion:
A harmonic oscillation having a constant amplitude and a constant frequency is called simple harmonic motion. In the absence of frictional force, the amplitude of the harmonic oscillator is constant.
A periodic function for which only Fourier coefficients a1 and b1 are non zero is called simple harmonic motion. Thus the equation of simple harmonic motion is given by
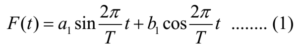
Let the displacement be y and

Substituting these values in equation (1)

Squaring and adding equation (2) and (3)

Dividing equation (3) by (2)

If the displacement is x then

Substituting these values in equation (4)

Dividing equation (5) by (6)

Notes:
The displacements of a particle performing S.H.M. are given by


Maximum values of sine and cosine functions are ±1. Thus the maximum displacement of a particle performing S.H.M. will be ±A. This maximum displacement of the particle performing S.H.M. is called the amplitude of S.H.M.
The term (ωt + Φo) is called a phase of S.H.M. and is denoted by letter Φ. The phase of S.H.M. always changes continuously with time but its initial phase remains constant.
Phase of S.H.M. = Φ = (ωt + Φo)
The term Φo is called the initial phase or epoch.
y = A sin (ωt + Φo)
at start t = 0 initial displacement y = yo.
∴ yo = A sin (ω(0) + Φo) = A sin Φo
∴ sin Φo =yo/A
∴ Φo = sin-1(yo/A )
If the particle starts from the equilibrium or the mean position Φo = 0
If the particle starts from the extreme position Φo = π/2
If Φo is changed to (π/2 + Φo) any one function, the two functions get interchanged into one another. Thus we conclude that the two functions differ by π/2.
Next Topic: Theory of Simple Harmonic Motion
