Science > Physics > Radiation > Concept of Black Body
In this article, we shall study the concept of a black body and its realization in practice.
Perfectly Black Body:
A body which absorbs all the radiant heat incident upon it is called a perfectly black body. Thus the coefficient of absorption of a perfectly black body is equal to 1. In fact, the blackness of such a body is due to the fact that it does not reflect or transmit any part of the heat incident upon it.
No body exists in nature, which can be called a perfectly black body. For practical purposes, lamp black which absorbs nearly 98 % of the heat incident upon it is considered as a perfectly black body.
Characteristics of Perfectly Black Body:
- A perfectly black body which absorbs all the radiant heat incident upon it.
- The coefficient of absorption for it is equal to 1.
- The blackness of such a body is due to the fact that it does not reflect or transmit any part of the heat incident upon it. Thus the coefficient of reflection and coefficient of transmission are zero.
Ferry’s Black Body:
A body which absorbs all the radiant heat incident upon it is called a perfectly black body.
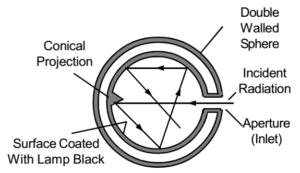
- Construction: It can be artificially constructed by taking a double-walled, hollow metal sphere having a small hole. The inner surface of the sphere is coated with lamp black and it has a conical projection on the opposite side of the hole.
- Working: The radiation entering the sphere through this hole suffers multiple reflections. During every reflection, about 98% of the incident radiant heat is absorbed by the sphere. Therefore the radiation is completely absorbed by the sphere within a few reflections. In this way, the sphere acts as a perfectly black body whose effective area is equal to the area of the hole.
Spectrum of a Black Body:
A black body emits radiations of all possible wavelengths from zero to infinity. These radiations are of electromagnetic nature. These radiations do not depend on the nature of the surface of the black body but depend only on its absolute temperature. Black body radiations extend over the whole range of wavelengths of electromagnetic waves. The distribution of energy over this entire range of wavelength or frequency is known as the black body radiation spectrum.
A sensitive instrument called bolometer is used to find energy density between the wavelengths λ and λ + dλ, By rotating the prism of the instrument this energy density is found for all the range of wavelengths at a constant high temperature of the perfectly black body.
Graphical representation:
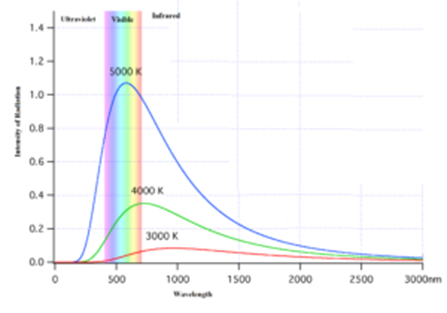
Characteristics of the Spectrum of a Black Body:
- The emissive power of a perfectly black body increases with an increase in its temperature for every wavelength.
- Each curve has characteristic form and each of them has a maxima i.e. maximum emissive power corresponding to a certain wavelength.
- The position of maxima shifts towards the ultraviolet region (shorter wavelength) with an increase in the temperature.
- λm T = Constant (Wien’s displacement law)
- The area under each curve gives the total radiant power per unit area of the black body at that temperature and it is directly proportional to T4 (Verification of Stefan’s law)
Wien’s Displacement Law:
For a black body, the product of its absolute temperature and the wavelength corresponding to maximum radiation of energy is constant.
Thus, λm T = Constant
The value of the constant of Wien’s displacement law is 2.898 x 10-3 mK.
Significance of Wien’s Displacement Law:
- This law can be used to surface the temperature of stars. This is the only method to determine the temperature of celestial bodies.
- It explains the colour change in solid on heating from dull red (longer wavelength) to yellow (shorter wavelength)to white (all wavelengths of visible spectra).
Simple Radiation Correction:
The specific heat of a solid or liquid is determined by the method of mixtures. The solid is heated to a high temperature. It is dropped in a calorimeter containing water (or liquid) at room temperature. Finally, the maximum temperature of the mixture is noted. Now as the temperature of the mixture begins to increase, the mixture begins to lose heat by conduction and radiation. Loss of heat by conduction can be minimized by surrounding the mixture by a bad conductor of heat such as cotton, wool, etc. However, the loss of heat by radiation cannot be stopped.
Therefore the maximum temperature of the mixture is always less than the temperature it would reach if radiation were absent. This correction to be made in the final temperature of the mixture is called radiation correction.
Method of Applying Radiation Correction:
A stopwatch is started at the moment the solid is dropped into the liquid and time t taken by the mixture to reach the maximum temperature is θ noted.
The mixture is then allowed to cool for time t / 2. Let ‘θ’ be the temperature of the mixture after time t / 2.
Then, radiation correction = Δθ = ½ (θ – θ )
Thus corrected maximum temperature of the mixture = θ + Δθ
Greenhouse Effect:
Earth’s surface absorbs thermal energy from the sun and becomes a source of thermal radiation. The wavelength of the radiation lies in the infrared region. A large part of the radiation is absorbed by greenhouse gases like carbon dioxide, methane, nitrous oxide, Chlorofluorocarbons, troposphere ozone. Due to which the atmosphere of the earth heats up and the atmosphere gives more energy to the earth resulting in a warmer surface.
The above process repeats until no radiations are available for absorption. This heating of the surface and the atmosphere of the earth is called the greenhouse effect. The significance of the greenhouse effect is that it keeps the earth warmer which leads to biodiversity. In the absence of this effect the temperature of the earth would be -18° C.
But due to human activities, the quantities of greenhouse gases are increasing rapidly making the earth warmer. This increase may disturb the life of plants and animals. It may result in the melting of ice in Polar Regions, which may lead to a rise in sea level submerging the coastal regions.
Previous Topic: Kirchhoff’s Law of Radiation
Next Topic: Stefan’s Law of Radiation