Numerical Problems on Keppler’s Laws

Science > Physics > Gravitation > Numerical Problems on Keppler’s Laws

In this article we shall study numerical problems on Keppler’s third law of orbital motion, to calculate period of revolution of a planet around the sun.

Example – 01:

What would be the length of the year if the earth were at half its present distance from the sun?

Given: r₂ = 1/2 r₁, old period T₁ = 365 days

To Find:  New period T₂ =?

Solution:

By Keppler’s law, we have T² ∝ r³

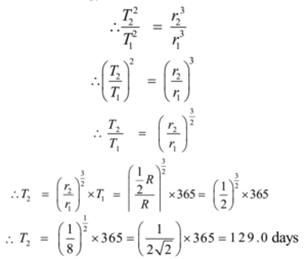
Ans: Thus length of the year would be 129 days

Example – 02:

What would be the duration of the year if the distance of the Earth from the sun gets doubled?

Given: r₂ = 2 r₁, old period T₁ = 365 days

To Find:  New period T₂ =?

Solution:

By Keppler’s law, we have T² ∝ r³

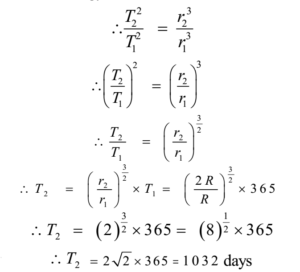
Ans: Thus the length of the year would be 1032 days

Example – 03:

Calculate the period of revolution of the planet Jupiter around the Sun. The ratio of the radius of Jupiter’s orbit to that of earth’s orbit around the Sun is 5.2.

Given: r_J : r_e  = 5.2 , Time period of the Earth  T₁ = 1 year.

To Find:  Period of Jupiter T_J =?

Solution:

By Keppler’s law, we have T² ∝ r³

Ans: The period of revolution of planet Jupiter is 11.86 years.

Example – 04:

A geostationary satellite is orbiting the earth at a height of 6R above its surface. What is the time period of a satellite orbiting at a height of 2.5 R above the earth’s surface? Where R is the radius of the Earth.

Solution:

Given: r₁ = R + 6R = 7R, r₂ = R + 2.5 R = 3.5 R, Time period of geostationary satellite T₁ = 24 hours.

To Find:  Period of second satellite T₂ =?

By Keppler’s law, we have T² ∝ r³

Ans: The period of revolution of a satellite orbiting at a height of 2.5 R above the earth’s surface is 8.458 hr.

Example – 05:

A satellite orbiting around the earth has a period of 8 hrs. If the distance of another satellite from the centre of the earth is four times that of above, what is its period?

Given: Ratio of radii of orbits r₁ = r, r₂ = 4r, Time period of first satellite  T₁ = 8 hours.

To Find:  Period of second satellite T₂ =?

Solution:

By Keppler’s law, we have T² ∝ r³

Ans: The period of the second satellite is 64 hours.

Example – 06:

Calculate the period of revolution of a planet around the sun if the diameter of its orbit is 60 times that of Earth’s orbit around the Sun. Assume both orbits to be circular.

Given: d_P = 60 d_E,  r_P =  60 r_E, Time period of Earth  T_E = 1 year.

To Find:  Period of the planet T_P =?

Solution:

By Keppler’s law, we have T² ∝ r³

Ans: The period of the planet is 464.8 years

Example – 07:

The planet Neptune travels around the sun with a period of 165 years. Show that the radius of its orbit is approximately thirty times that of the Earth.

Given: Period of NeptuneT_N = 165 years, Time period of Earth  T_E = 1 year.

To Show:  Radius of Neptune r_N =30 r_E

Solution:

By Keppler’s law, we have T² ∝ r³

Ans: Thus the radius of its orbit is approximately thirty times that of the Earth.

Example – 08:

The radius of earth’s orbit is 1.5 ×10⁸ km and that of mars is 2.5 × 10¹¹ m. in how many years the mars completes its one revolution.

Given: Radius of the orbit of the Earth r_E = 1.5 ×10⁸ km = 1.5 ×10¹¹ m, Radius of the orbit of the Mars r_M = 2.5 ×10¹¹ m, Time period of Earth T_E = 1 year.

To Find:  Time period of Mars T_M =?

Solution:

By Keppler’s law, we have T² ∝ r³

T_M = 2.15 years

Ans: In 2.15 years Mars completes its one revolution.

Example – 09:

The mean distance of the earth from the Sun is 1.496 ×10⁸ km and its period of revolution around the Sun is 365.3 days. The time periods of revolutions of planets Venus and Mars are 224.7 days and 687.0 days respectively, where day means a terrestrial day. Calculate the distances of Venus and Mars from the Sun.

Given: Radius of the orbit of the Earth r_E = 1.496 ×10⁸ km, Time period of Earth T_E = 365.3 days, Time period of Venus  T_E = 224.7 days, Time period of Mars  T_M = 687.0 days.

To Show:  Radius of the orbit of the Venus r_V =? Radius of the orbit of the Mars r_M = ?,

Solution:

By Keppler’s law, we have T² ∝ r³

Ans: Distance of Venus from the sun is 1.08 ×10⁸ km and distance of Mars from the sun is 2.279 ×10⁸ km

Example – 10

Suppose Earth’s orbital motion around the Sun is suddenly stopped. What time the Earth shall take to fall into the Sun.

Given: Radius of the orbit of the Earth = r, Time period of Earth T = 365 days,

To Show:  Time taken by the Earth to fall into the Sun T₂ = ?,

Solution:

In this problem, we are assuming there is no effect of temperature on the Earth. If the Earth suddenly stops rotating around the sun and falls into the sun and let us assume it comes back to the point on the orbit. Thus it starts orbiting along a highly flattened ellipse with major axis  = r. Thus semimajor axis = a = r₂ = r/2

By Keppler’s law, we have T² ∝ r³

This is the total period of revolution. It should take half the time period to fall into the Sun

Time required = 130/2 = 65 days

Ans: Earth shall take 65 days to fall into the Sun.

Note: Thus, in general, the time taken by a planet to fall into the sun = Period x 0.1768 (This relation can be used for MCQ)

Previous Topic: Keppler’s Laws of Orbital Motion

Next Topic: Satellites and Their Uses

Science > Physics > Gravitation > Numerical Problems on Keppler’s Laws