Numerical Problems on Critical Velocity and Period of Satellite – 02

Science > Physics > Gravitation > Numerical Problems on Critical Velocity and Period of Satellite

Example – 18:

A satellite revolves around a planet of the mean density of 10⁴ kg/m³. If the radius of its orbit is only slightly greater than the radius of the planet, find the time of revolution of the satellite. G = 6.67 x 10^-11S. I.  units.

Given: Density of material of planet = ρ = 10⁴ kg/m³, G = 6.67 x 10^-11 N m²/kg² ;

To Find: Period of Satellite = T =?

Solutions:

The time period of a satellite orbiting around the earth is given by

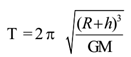
If satellite orbiting very close to the earth  (i.e. h < < R) then h can be neglected. Then R + h = R

Ans: Time of revolution of the satellite is 1.044 hr

Example – 19:

What would be the speed of a satellite revolving in a circular orbit close to the earth’s surface? Given G = 6.67 x 10^-11 S.I. units; density of earth’s matter = 5500 kg/m³ and radius of earth = 6400 km.  Also, find its period.

Given: density of erth’s matter = ρ = 5500 kg/m³, radius of earth = R = 6400 km = 6.4 x 10⁶ m, G = 6.67 x 10^-11 N m²/kg² ;

To Find: orbital velocity = v_c = ?, period = T = ?

Solution:

If satellite orbiting very close to the earth  (i.e. h < < R) then h can be neglected. Then R + h = R

The time period of a satellite orbiting around the earth is given by

T = 2πR/v_c =  2 x 3.142 x 6400 /7.931 = 5071 s

T = 5071/3600 = 1.408 h

Ans: The speed of the satellite is 7.931 km/s and the time of revolution of the satellite is 1.408 h.

Example – 20:

The mean angular velocity of the earth around the sun is 1° per day. The distance from the sun to the earth is 1.5 x 10⁸ km. Determine the mass of the sun. G = 6.67 x 10^-11 S.I. units.

Given: Angular frequency = ω = 1° per day, radius of orbit = r = 1.5 x 10⁸ km = 1.5 x 10¹¹ m, G = 6.67 x 10^-11 S.I. units.

To find: the mass of sun = M =?

Solution:

∴ T = 2 x 24 x 60 x 60 x 180    s

∴ M = 2.062 x 10³⁰ kg

Ans: Mass of the sun is 2.062 x 10³⁰ kg

Example – 21:

Find the mass of the sun given that the radius of earth’s orbit is 1.5 x 108km. G = 6.67 x 10-11 S. I. units and the period of earth’s revolution around the sun is 365 days.

Given: Period of revolution = T= 365 days = 365 x 24 x 60 x 60 s, Radius of orbit = r = 1.5 x 10⁸ km = 1.5 x 10¹¹ m, G = 6.67 x 10^-11 S.I. units.

To find: the mass of sun =M =?

Solution:

∴ M = 2.062 x 10³⁰ kg

Ans: Mass of the sun is 2.062 x 10³⁰ kg

Example – 22:

If the moon revolves around the earth once in 27 days and 7 hours in an orbit which is 60 times the earth’s radius, find g at the earth’s surface. R= 6400 km.

Given: radius of earth = R = 6400 km = 6.4 x 10⁶ m, radius of orbit of moon = r = 60 R , Period of revolution of ,moon = 27 days 7 hours =  = 27 x 24 x 60 x 60+ 7 x 60 x 60 =6556060 s,

To find: acceleration due to gravity = g = ?

Solution:

Ans: g on the Earth’s surface = 9.81 m/s²

Example – 23:

Assuming that the moon describes a circular orbit of radius R about the earth in 27 days and that Titan describes a circular orbit of radius 3.2 R about Saturn in 16 days, compare the mass of Saturn and the earth.

Given: Period of Moon =T_M= 27 days, radius of orbit of moon = r_M = R, time period of titan = T_T =16 days, radius of orbit of titan = r_T = 3.2 R,

To Find:   Ratio of mass of saturn to the earth = M_S /M_E=?

Solution:

Ans: The ratio of the mass of Saturn to the earth is 93.3 :1

Example – 24:

A satellite of mass 1750 kg is moving around the earth in an orbit at a height of 2000 km from the surface of the Earth. Find its angular momentum given G = 6.67 x 10^-11 Nm² kg^-2 and mass of the  earth = 6 x  10²⁴ kg.

Given: h = 2000 km, hence radius of orbit = r = R + h = 6400 + 2000 = 8400 km = 8.4 x 10⁶ m, G = 6.67 x 10^-11 Nm² kg^-2 ; mass of satellite = m = 1750 kg, mass of the earth = M = 6 x  10²⁴ kg;

To find: Angular momentum = L= ?,

Solution:

Ans : The angular momentum of the satellite is 1.015x 10¹⁴ kg m² s^-1.

Example – 25:

The radii of the orbits of two satellites revolving around the earth are in the ratio 3:8. Compare their i) critical speed and ii) periods.

Given: ratio of radii of orbits r₁ :  r₂  =  3:8

To find: v_c1 : v_c2  =? , T₁ : T₂ = ?

Solution:

Ans : The ratio of their critical velocities is 1.633:1, The ratio of their period is 0.2296:1

Example – 26:

The distances of two planets from the sun are 10¹³ m 10¹² m respectively. Find the ratio of their periods and orbital speeds.

Given: r₁ = 10¹³ m ,  r₂ = 10¹² m

To find: T₁ : T₂ = ?, v_c1 : v_c2 = ? ,

Solution:

Ans: The ratio of their period is 31.62:1, The ratio of their critical velocities is 0.3162:1

Example – 27:

Two satellites X and Y are moving in circular orbits of radii r and 2r respectively around the same planet. What is the ratio of their critical velocities?

Given: r_X = r, r_Y = 2r.

To find: v_cX : v_cY  =?

Solution:

Ans: The ratio of their critical velocities is √2 : 1

Example – 28:

A communication satellite is at a height of 36400 km from the surface of the earth. What will be its new period when it is brought down to the height of 20000 km from the surface of the earth? The radius of the earth is 6400 km.

Given: Initial radius of orbit = r₁ = 36400 + 6400 = 42800 km, Final radius of orbit = r₂=   6400 + 20000 = 26400 km, Initial time period of satellite = T₁ =24 hr,

To Find:   New time period of satellite = T₂ =?

Solution:

By Keppler’s law

∴ T₂ = 11.62 h

Ans: The new period of satellite 11.62 hr

Example – 29:

A satellite at a height of 2725 km makes ten revolutions around the earth per day. What is the number of revolutions made per day by a satellite orbiting at a height of 560 km? Radius of earth = 6400 km.

Given: radius of orbit of earth = R = 6400 km, height of satellite above the surface of earth in first case = h₁ = 2725 km, height of satellite above the surface of earth in second case = h₂ = 560 km, number of revolutions of satellite in first case = n₁ = 10 per day

To Find: number of revolutions of satellite in second case = n₂ =?

Solution: 

r₁ = R + h₁ = 6400 + 2725 = 9125 km

r₂ = R + h₂ = 6400 +560 = 6960 km

Ans: The satellite will make 15 revolutions per day.

Example – 30:

India’s most powerful rocket (PSLV) projected a remote sensing 850 kg satellite into an orbit 620 km above the earth’s surface. Assuming that the orbit is circular, find its speed and calculate the number of complete revolutions it makes around the earth in one day. g = 9.8 m/s² and R = 6400 km.

Given: h = 620 km, radius of orbit of satellite = r = R + h = 6400 + 620 = 7020 km = 7.02 x 10⁶ m, g = 9.8 m/s², R = 6400 km  = 6.4 x 10⁶ m

To find: speed of satellite = v_c = ?, N = ?

Solution:

N = 14.81 revolutions per day

Ans: The speed of satellite = 7.561 km/s and number of revolutions of satellite per day = 14.81

Example – 31:

A satellite going in a circular orbit of radius 4 x 10⁴ km around the earth has a certain speed. If this satellite were to move around Mars with the same speed, what would be its orbital radius? The masses of earth and mars are in the ratio of 10:1 and their radii are in the ratio 2:1

Given: speeds are same v_cE = v_cM, radius of satellite around the earth = r_E = 4 x 10⁴ km, M_E:M_M = 10:1 and R_E:R_M = 2:1

To find: radius of the satellite around the mars =r_M =?

Solution:

Ans: Radius of the satellite around Mars is 4000 km.

Example – 32:

Two satellites orbiting around the earth have their initial speeds in the ratio 4 : 5. Compare their orbital radii.

Given: ratio of speeds v_c1 : v_c2  =  4 : 5

To find: r₁ :  r₂  = ?

Solution:

The critical velocity of a satellite orbiting around the earth is given by

Ans : The ratio of their radii is 25 : 16

Example – 33:

Compare the critical speeds of two satellites if the ratio of their periods is 8 : 1.

Given: T₁/T₂ = 8/1

To Find: Ratio of critical velocity = v_c1/v_c2 =?,

Solution:

From equations (1) and (2)

Ans: The ratio of their critical velocities is 1:2

Example – 34:

Calculate the height of communication satellite above the surface of the earth? Given G = 6.67 x 10^-11 N m²/kg²; radius of earth = 6400 km, Mass of the earth = 6 x 10²⁴ Kg

Given: For communication satellite, T = 24 hr = 24 x 60 x 60 s, Universal gravitational Constant = G = 6.67 x 10^-11 N m²/kg²; radius of earth = R = 6400 km = 6.4 x 10⁶ m, Mass of the earth = M = 6 x 10²⁴ Kg

To Find: height of communication satellite above the surface of the earth = h = ?

Solution:

The time period of satellite is given by

Now, r = R + h
Hence, h = r – R = – 6.37 x 106
= 35.95 x 106 m
= 35.95 x 103 x 103 m
= 35950 km
Ans: The height of satellite above the surface of the earth is 35950 km.

Previous Topic: More Problems on Critical Velocity

Next Topic: Binding Energy of Satellite

Science > Physics > Gravitation > Numerical Problems on Critical Velocity and Period of Satellite