Science > Physics > Kinetic Theory of Gases > Pressure Exerted by Gas
In this article, we shall study to derive an expression for pressure exerted by gas on the walls of container. We shall also derivation of different gas laws using the kinetic theory of gases.
Expression for Pressure Exerted by a Gas Using Kinetic Theory of Gases:
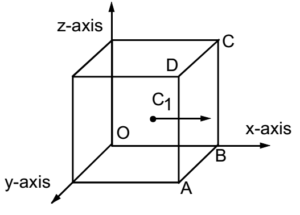
Let us consider a gas enclosed in a cube whose each edge is of length ‘l’. Let A be the area of each face of the cube. So A = l². Let V be the volume of the cube (or the gas). So V = l³. Let ‘m’ be the mass of each molecule of the gas and ‘N’ be the total number of molecules of the gas and ‘M’ be the total mass of the gas. So M = mN.
Suppose that the three intersecting edges of the cube are along the rectangular co-ordinate axes X, Y and Z with the origin O at one of the corners of the cube. By the kinetic theory of gases, we know that molecules of a gas are in a state of random motion so it can be imagined that on an average N/3 molecule are constantly moving parallel to each edge of the cube i.e. along the co-ordinate axes. Let velocities of N/3 molecules moving parallel to X-axis be C1, C2, C3, …. , CN/3 respectively.
Consider a molecule moving with the velocity C1in the positive direction of the X-axis. The initial momentum of the molecule,
p1 = mC1,
It will collide normally with the wall ABCD and as the collision is perfectly elastic rebounds with the same velocity. Hence, momentum of molecule after collision,
p2 = – mC1
Change in the momentum of the molecule due to one collision with ABCD
Δp = p2 – p1
Δp = – mC1 – mC1 = – 2 – mC1
Before the next collision with the wall ABCD the molecule will travel a distance 2l with velocity C1. So time interval between two successive collisions of the molecule with ABCD = 2l /C1
Number of collisions of the molecule per unit with wall ABCD = C1/ 2l
Change in the momentum of the molecule per unit time
= – 2mC1 × C1/ 2l = – mC1² /l
But by Newton’s second law we know that the rate of change of momentum is equal to the impressed force.
So force exerted on the molecule by wall ABCD =- mC1² /l
From Newton’s third law of motion, action and reaction are equal and opposite. So force exerted on the molecule by wall ABCD = mC1² /l. Thus every molecule will exert a force on the wall ABCD. So total force exerted on the wall ABCD due to molecules moving in the positive X-axis direction is given by

Let P be the pressure of the gas. The pressure exerted on the wall ABCD is given by
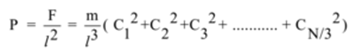
The pressure exerted on each wall will be the same and i.e. equal to the pressure of the gas. By definition of r.m.s. velocity

This is an expression for pressure exerted by a gas on the walls of the container.
Boyle’s Law from Kinetic Theory of Gases:
Statement:
The temperature remaining constant the pressure exerted by a certain mass of gas is inversely proportional to its volume.
Explanation:
If P is the pressure and V is the volume of a certain mass of enclosed gas, then
P ∝1 / V ∴ P V = constant
Proof:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas

N = Number of molecules of a gas
m = Mass of each molecule of a gas.
But by assumptions of the kinetic theory of gases the average kinetic energy of a molecule is constant at a constant temperature. Thus the right-hand side of the equation is constant.
Thus, PV = constant i.e. P ∝ 1 / V . This is Boyle’s Law.
Thus Boyle’s law is deduced from the kinetic theory of gases.
Relation Between r.m.s. Velocity of Gas Molecule and the Absolute Temperature of the Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas
For one mole of a gas, the total mass of the gas can be taken as molecular weight

This is an expression for r.m.s. velocity of gas molecules in terms of its molecular weight. Now R is the universal gas constant, molecular mass M for a particular gas is constant.

Thus, the R.M.S. velocity of a gas is directly proportional to the square root of the absolute temperature of the gas.
Kinetic Energy of Gas:
Kinetic Energy Per Unit Volume of a Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas

N = Number of molecules of a gas
m = Mass of each molecule of a gas.

This is an expression for the kinetic energy of gas molecules per unit volume of the gas.
Kinetic Energy of a Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas

N = Number of molecules of a gas
m = Mass of each molecule of a gas.

This is an expression for the kinetic energy of gas molecules.
Average Kinetic Energy Per Mole of a Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas
For one mole of a gas, the total mass of the gas can be taken as molecular weight

This is an expression for r.m.s. velocity of gas molecules in terms of its molecular weight. Now R is the universal gas constant, molecular mass M for a particular gas is constant.

This is an expression for kinetic energy per mole of a gas
Average Kinetic Energy Per Molecule of a Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas
For one mole of a gas, the total mass of the gas can be taken as molecular weight

This is an expression for r.m.s. velocity of gas molecules in terms of its molecular weight. Now R is the universal gas constant, molecular mass M for a particular gas is constant.

This is an expression for kinetic energy per mole of a gas

Where N = Avogadro’s number
This is an expression for average kinetic energy per molecule of a gas.
Average Kinetic Energy Per Unit Mass of a Gas:
From kinetic theory of gases, the pressure exerted by a gas is given by

Where M = Total mass of the gas = Nm
V = Volume of the gas
ρ = Density of the gas
C̅ = r.m.s. velocity of gas molecules.
M = Molecular mass of the gas
For one mole of a gas, the total mass of the gas can be taken as molecular weight

This is an expression for r.m.s. velocity of gas molecules in terms of its molecular weight. Now R is the universal gas constant, molecular mass M for a particular gas is constant.

This is an expression for kinetic energy per mole of a gas

This is an expression for average kinetic energy per unit mass of a gas.
Charle’s Law:
At constant pressure, the volume of a certain mass of enclosed gas is directly proportional to the absolute temperature of the gas.

Dalton’s Law of Partial Pressure:
At constant temperature, the pressure exerted by a mixture of two or more non-reacting gases in enclosed in a definite volume, is equal to the sum of the individual pressure which each gas exerts, if present alone in the same volume.
Explanation: Let P1, P2, P3, …. be the partial pressure of the mixture of non-reacting gases enclosed in a definite volume and at temperature T. Let P be the pressure of a mixture of these gases. Then by the law of partial pressure,
P = P1 + P2 + P3, ….
Maxwell Distribution of Molecular Speeds:
For a given mass of a gas, the velocities of all molecules are not the same, even when bulk parameters like pressure, volume and temperature are fixed. Collisions change the direction and speed of the molecules, but in a state of equilibrium, the distribution of speed is constant.
It is observed that the molecular speed distribution gives the number of molecules dN(v) between speeds v and v + dv, which is proportional to dv (difference in velocities) is called Maxwell distribution.
Following graph shows the distribution of velocity at different temperatures.

The fraction of the molecules with speed v and v + dv is equal to the area of the strip shown.
Previous Topic: Assumptions of Kinetic Theory of Gases
Next Topic: Numerical Problems on Kinetic Theory