More Problems on Form of Physical Equation

Science > Physics > Units and Measurements > Form of Physical Equation

In this article, we shall study the use of principle of homogeneity to derive the form of the physical equation.

Example – 01:

The hydrostatic pressure P of a liquid column depends upon density (d) and height of liquid (h) and acceleration due to gravity (g), using dimensional analysis derive the formula for pressure.

Solution:

let  P  ∝  d^x,   P  ∝  h^y,   P  ∝  g^z,

Combining above relations we have  P  ∝  d^x h^y g^z,

P  = k  d^x h^y g^z …………..  (1)

By principle of homogeneity of dimensions we have

[P]  = [d]^x  [h]^y [g]^z 

∴  [L^-1M¹T^-2]  = [L^-3M¹T⁰]^x  [L¹M⁰T⁰]^y [L¹M⁰T^-2]^z 

∴  [L^-1M¹T^-2]  = [L^-3xM^xT⁰][L^yM⁰T⁰][L^zM⁰T^-2z]

∴  [L^-1M¹T^-2]  = [L^{-3x + y + z} M^xT^-2z]

Considering equality of two sides we have

3x +y +z = -1 , x = 1 , -2z = -2 i.e. z = 1

∴ 3x +1+1 = -1

∴ 3x  = – 3

∴ x  = 1

Substituting x =1, y = 1 and z = 1 in equation (1) we get

P  = k  dh g

The value of constant in this case is 1, i.e. k = 1

P  = h d g

This is the formula for the pressure

Example – 02:

Derive an expression for kinetic energy of a body of mass ‘m’ moving with a velocity ‘v’, using dimensional analysis. Or Using dimensional analysis, show that the kinetic energy of a body of mass m moving with a velocity v varies as mv².

Solution:

Let us represent kinetic energy by a symbol E

let  E  ∝  m^x,   E  ∝  v^y

Combining above relations we have  E  ∝  m^x v^y 

E  =  k m^x v^y   …………..  (1)

By the principle of homogeneity of dimensions we have

[E]  = [m]^x  [v]^y 

∴  [L²M¹T^-2]  = [L⁰M¹T⁰]^x  [L¹M⁰T^-1]^y

∴  [L²M¹T^-2]  = [L⁰M^xT⁰][L^yM⁰T^-y]

∴  [L²M¹T^-2]  = [L^yM^xT^-y]

Considering the equality of two sides we have

y = 2 and x = 1

Substituting x =1 and y = 2 in equation (1) we get

E  =  k m¹ v²

This is the form of the equation for the kinetic energy of a body.

E ∝  m v²

Ans: Thus the kinetic energy of a body varies as mv².

Example – 03: 

The frequency ‘n’ of vibration of a wire under tension depends on tension ‘T’, mass per unit length ‘m’ and vibrating length ‘l’ of wire. Using dimensional analysis, obtain dependence of frequency on these quantities. OR The frequency n of vibration of a string of length l under tension T depends upon l, T and m where m is the mass per unit length of the string. Show that

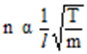
Solution:

Given  n  ∝  T^x,   n  ∝  m^y and n  ∝  l^z

Combining above relations we have  n  ∝  T^x m^y l^z

n  =  k T^x m^y l^z   …………..  (1)

By the principle of homogeneity of dimensions we have

[n]  =  [T]^x [m]^y [l]^z

∴  [L⁰M⁰T^-1]  = [L¹M¹T^-2]^x [L^-1M¹T⁰]^y  [L¹M⁰T⁰]^z

∴  [L⁰M⁰T^-1]  = [L^xM^xT^-2x][L^-yM^yT⁰][L^zM⁰T⁰]

∴  [L⁰M⁰T^-1]  = [L^{x – y+ z}M^{x + y}T^-2x]

Considering the equality of two sides we have

x – y + z = 0, x + y = 0 and – 2x = -1

∴ x = 1/2

Substituting in x + y = 0

1/2 + y = 0

∴ y = – 1/2

Substituting x = 1/2 and y = -1/2 in x – y + z = 0

∴  1/2 – (-1/2) + z = 0

∴ 1 + z = 0

∴ z = -1

Substituting x =1/2, y = -1/2 and z = – 1 in equation (1) we get

n  =  k T^1/2 m^-1/2 l^{– 1}

n  ∝    T^1/2 m^-1/2 l^{– 1}

n  ∝   (l^{– 1}) (T^1/2 /m^1/2)

n  ∝   (1/l) (T/m)^1/2

Proved as required

Example – 04:

For a small sphere falling through a viscous medium of infinite extent, the force(F) opposing the motion depends directly upon the velocity (v) coefficient of viscosity (η) of the medium and the radius (r) of the sphere. From the dimensional analysis, show that F = 6πηrv. where the constant k = 6π.

Solution:

Given  F  ∝  v^x,   F  ∝ η^y and F  ∝  r^z

Combining above relations we have  F  ∝  v^x η^y r^z

F  =  k v^x η^y r^z   …………..  (1)

By the principle of homogeneity of dimensions we have

[F]  =  [v]^x [η]^y [r]^z

∴  [L¹M¹T^-2]  = [L¹M⁰T^-1]^x [L^-1M¹T^-1]^y  [L¹M⁰T⁰]^z

∴  [L¹M¹T^-2]  = [L^xM⁰T^-x][L^-yM^yT^-y][L^zM⁰T⁰]

∴  [L¹M¹T^-2]  = [L^{x – y + z}M^yT^{-x – y}]

Considering the equality of two sides we have

x – y + z = 1,  y = 1 and x – y = – 2

Substituting y = 1 in x – y = 0

x – 1 = 0

∴ x = 1

Substituting x = 1 and y =1 in x – y + z = 1

∴ 1 – 1 + z = 1

∴ z = 1

Substituting x =1, y = 1 and z = 1 in equation (1) we get

F  =  k v¹ η¹ r ¹

Given k = 6π

∴  F = 6πηrv

Example – 05:

Using dimensional analysis, show that the velocity ‘v’ of a body falling freely under gravity varies with √gh . where ‘g’ is the acceleration due to gravity and ‘h’ is the distance through which the body falls.

Solution:

Given  v  ∝  g^x and   v ∝ h^y 

Combining above relations we have  v  ∝  g^x h^y

v  =  k g^x h^y   …………..  (1)

By the principle of homogeneity of dimensions we have

[v]  =  [g]^x [h]^y

∴  [L¹M⁰T^-1]  = [L¹M⁰T^-2]^x [L¹M⁰T⁰]^y

∴  [L¹M⁰T^-1]  = [L^xM⁰T^-2x][L^yM⁰T⁰]

∴  [L¹M⁰T^-1]  = [L^{x + y} M⁰T^-2x ]

Considering the equality of two sides we have

x + y = 1 and  – 2x = -1 i.e. x = 1/2

Substituting  in x + y = 1

1/2 + y = 1

∴ y =  1/2

Substituting x = 1/2 and y = 1/2  in equation (1) we get

v  =  k g^1/2 h^1/2 

∴ v  =  k (g h)^1/2 

∴ v  =  k √gh 

∴ v  ∝ √gh

Ans: The velocity ‘v’ of a body falling freely under gravity varies with √gh .

Example – 06:

The period T of revolution of the earth around the sun depends upon the orbital radius ‘R’, the mass ‘M’ of the Sun and gravitational constant ‘G’. Show by dimensional analysis that T² ∝ R³.

Solution:

Given  T  ∝  R^x,   T  ∝ M^y and T ∝  G^z

Combining above relations we have  T  ∝  R^x M^y G^z

T  =  k R^x M^y G^z   …………..  (1)

By the principle of homogeneity of dimensions we have

[T]  =  [R]^x [M]^y [G]^z

∴  [L⁰M⁰T¹]  = [L¹M⁰T⁰]^x [L⁰M¹T⁰]^y  [L³M^-1T^-2]^z

∴  [L⁰M⁰T¹]  = [L^xM⁰T⁰][L⁰M^yT⁰][L^3zM^-zT^-2z]

∴  [L⁰M⁰T¹]  = [L^{x + 3z} M^{y – z}T^-2z]

Considering the equality of two sides we have

x + 3z = 0, y – z = 0, -2z = 1 i.e. z = – 1/2,

Substituting z = – 1/2 in y – z = 0

∴ y – (-1/2) = 0

∴ y = -1/2

Substituting z = -1/2 in x + 3z = 0

∴ x + 3(-1/2) = 0

∴ x + – 3/2 = 0

∴ x = 3/2

Substituting x = 3/2, y = -1/2 and z = -1/2 in equation (1) we get

T  =  k R^3/2 M^-1/2 G ^-1/2

Squaring both the sides we get

T²  =  k² R³ M^-1 G ^-1

T²  =  k² (R³/GM)

Now the mass of the Sun M and G are constant

∴ T² ∝ R³

Example – 07:

The velocity v of sound in a gas depends upon the pressure P and density ρ, show by dimensional analysis that v ∝ √P/ρ.

Solution:

Given  v  ∝  P^x and   v ∝ ρ^y 

Combining above relations we have  v  ∝  P^x ρ^y

v  =  k P^x ρ^y   …………..  (1)

By the principle of homogeneity of dimensions we have

[v]  =  [P]^x [ρ]^y

∴  [L¹M⁰T^-1]  = [L^-1M¹T^-2]^x [L^-3M¹T⁰]^y

∴  [L¹M⁰T^-1]  = [L^-xM^xT^-2x][L^-3yM^yT⁰]

∴  [L¹M⁰T^-1]  = [L^{– x – 3y} M^{x + y}T^-2x ]

Considering the equality of two sides we have

x – 3y = 1, x + y = 0 and  – 2x = -1 i.e. x = 1/2

Substituting  in x + y = 0

1/2 + y = 0

∴ y =  -1/2

Substituting x = 1/2 and y = 1/2  in equation (1) we get

v  =  k P^1/2 ρ^-1/2 

∴ v  =  k (P/ρ)^1/2 

∴ v  =  k √P/ρ 

∴ v  ∝ √P/ρ 

Example – 08:

Reynold’s number R which determines the condition for streamline flow of a liquid through a tube depends upon the velocity ‘v’ of the liquid flow, the density ‘ρ’ of liquid, coefficient of viscosity of liquid ‘η’ and diameter ‘d’ of the tube. Using dimensional analysis show that R ∝ vρd/η.

Solution:

Example – 09:

Assuming a period of vibration of a tuning fork depends upon a length l of its prongs. density rho of the material and elastic constant E of the material. Find the formula for the period of vibrations using dimensional analysis?

Solution:

Previous Topic: Problems on Dimensional Analysis

Next Topic: Concept of Significant Figures

Science > Physics > Units and Measurements > Form of Physical Equation