Numerical Problems on S.H.M.- 01

Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on Displacement, Velocity, and Acceleration of Particle Performing S.H.M.

in this article, we shall study to calculate the initial phase, displacement, velocity, and acceleration of a body performing S.H.M.

Example – 1:

A particle performs a linear S.H.M along a path 10 cm long. The particle starts from a distance of 1 cm from the mean position towards the positive extremity. Find the epoch and the phase of motion when the displacement is 2.5 cm.

Given:  Path length = 10 cm, amplitude = path length /2 = 10/2 = 5 cm, Initial displacement = x₀ = 1 cm, Displacement = x = 2.5 cm.

To Find: Epoch = α =? and phase of S.H.M. = (ωt + α) = ?

Solution:

Epoch = α = sin^-1(x_o/a) = sin^-1(1/5) = sin^-1(0.2) = 11°32’

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  2.5 = 5 sin (ωt + α)

∴  sin (ωt + α) = 2.5/5 = 1/2

∴  (ωt + α) = sin^-1(1/2) = π/6

Ans: Initial phase is 11°32’ and phase of S.H.M. is π/6 or 30^o.

Example – 2:

The periodic time of a body executing S.H.M. is 2 s. After how much time interval from t =0 will its displacement be half the amplitude?

Given: Time period = T = 2 s, Displacement x = 1/2 a, particle passes through mean position, α = 0.

To Find: Time elapsed = t =?

Solution:

Angular velocity = ω = 2π/T = 2π/2 = π rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  1/2 a = a sin (πt + 0)

∴  1/2 =sin (πt)

∴  πt = sin^-1(1/2) = π/6

∴  t = 1/6 s

Ans: After 1/6 s the displacement will be half the amplitude

Example – 3:

A particle executes S.H.M.  of amplitude 25 cm and time period 1/3 seconds. What is the minimum time required for a particle to move between two points located at a distance of 12.5 cm on either side of the mean position?

Given: amplitude = a = 25 cm, x = 12.5 on either side, Period = T = 3 s, particle passes through mean position, α = 0.

To Find: Time required = 2t = ?

Solution:

Angular velocity = ω = 2π/T = 2π/3  rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  12.5 = 25 sin ((2π/3)t + 0)

∴  1/2 =sin ((2π/3)t)

∴  (2π/3)t = sin^-1(1/2) = π/6

∴  t = 1/4 s

Now the points are on either side of the mean position

Hence time taken to move between these two points = 2t = 2 x 1/4 = 0.5 s

Ans: the minimum time required is 0.5 s

Example – 4:

A particle executes S.H.M. of period 12 s and of amplitude 8 cm. What time will it take to travel 4 cm from the extreme position ?

Given: Period = T = 12 s, amplitude = a = 8cm, distance from extreme position = 4 cm, displacement = x = 8 cm – 4 cm = 4 cm, particle starts from extreme position, α = π/2.

To Find: time taken = t = ?, Velocity = v = ?

Solution:

Angular velocity = ω = 2π/T = 2π/12  = π/6 rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  4 = 8 sin ((π/6)t + π/2)

∴  1/2 =cos ((π/6)t)

∴  (π/6)t = cos^-1(1/2) = π/3

∴  t = 2 s

Ans: Time taken = 2 s

Example – 5

A particle performs S.H.M. of period 4 s. If the amplitude of its oscillations is 4 cm, find the time it takes to describe 1 cm from the extreme position.

Given: Period = T = 4 s, amplitude = a = 4cm, distance from extreme position = 1 cm, displacement = x = 4 cm – 1 cm = 3 cm, particle starts from extreme position, α = π/2.

To Find: time taken = t = ?

Solution:

Angular velocity = ω = 2π/T = 2π/4  = π/2 rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  3 = 4 sin ((π/2)t + π/2)

∴  3/4 = cos ((π/2)t)

∴  (π/2)t = cos^-1(3/4) = 41.41° = 41.41 x 0.0175= 0.7247 rad

∴  t = 0.7247 x 2 /3.142 = 0.4613 s

Ans:  Time taken = 0.4613 s

Example – 6

A particle performs S.H.M. of period 12 s along a path 16 cm long. If it is initially at the positive extremity, how much time will it take to cover a distance of 6 cm from that position?

Given: Period = T = 12 s, path length = 16 cm, amplitude = a = 16/2 = 8cm, distance from extreme position = 6 cm, displacement = x = 8 cm – 6 cm =2 cm, particle starts from extreme position, α = π/2.

To Find: time taken w.r.t. extreme position = t_e = ?

Solution:

Angular velocity = ω = 2π/T = 2π/12  = π/6 rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  2 = 8 sin ((π/6)t + π/2)

∴  2/8 = cos ((π/6)t)

∴  (π/6)t = cos^-1(1/4) = 75.52° =75.52 x 0.0175 = 1.322 rad

∴  t = 1.322 x 6 /3.142 = 2.52 s

Ans: Time taken =2.52 s

Example – 7:

The shortest distance traveled by a particle performing S.H.M. from its mean position in 2 seconds is equal to √3/2  of its amplitude. Find its period.

Given: Time elapsed = t = 2s, displacement = x = a √3/2, particle passes through mean position, α = 0.

To Find: Period = T = ?

Solution:

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  a √3/2  = a sin (ωt + 0)

∴  √3/2  = sin ωt

∴  ωt = sin^-1(√3/2 ) = π/3

∴  (2π/T)t = π/3

∴  (2π/T)x 2 = π/3

∴  T = 2 x 2 x 3 = 12 s

Ans: Period is 12 s

Example – 8:

A particle performing S.H.M. has a period of 6 s and amplitude of 8 cm. The particle starts from the mean position and moves towards the positive extremity. Find its displacement, velocity, and acceleration 0.5 s after the start.

Given:  Period = T = 6 s, amplitude = a = 8cm, time elapsed = t = 0.5 s, particle starts from mean position, α = 0.

To Find: Displacement = x = ?, Velocity = v =?, acceleration = f = ?

Solution:

Angular velocity = ω = 2π/T = 2π/6 = π/3 rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  x = 8 sin ( π/3 x 0.5 + 0)

∴  x = 8 sin ( π/6) = 8 x 1/2 = 4 cm

The magnitude of the velocity of a particle performing S.H.M. is given by

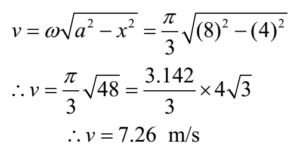
The magnitude of the acceleration of a particle performing S.H.M. is given by

f = ω²x = (π/3)² x 4 =  (3.142/3)² x 4 = 4.38 cm/s².

Ans: Displacement = 4 cm; velocity = 7.26 cm/; acceleration = 4.38 cm/s²

Example – 9:

A sewing machine needle moves in a path 4 cm long and the frequency of its oscillations is 10 Hz. What are its displacement and acceleration 1/120 s after crossing the centre of its path?

Given: Path length = 4 cm, amplitude = path length/2 = 4/2 = 2 cm, Frequency of oscillation = n = 10 Hz, Time elapsed = t = 1/120 s,  particle passes through mean position, α = 0.

To Find: Displacement = x =? acceleration = f =?

Solution:

Agular velocity = ω = 2πn = 2π x 10 = 20π rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴  x = 2 sin ( 20π x 1/120 + 0)

∴  x = 2 sin ( π/6) = 2 x 1/2 = 1 cm

The magnitude of the acceleration of a particle performing S.H.M. is given by

f = ω²x = (20π)² x 1 =  (20 x 3.142)² = 3944 cm/s².

Ans: Displacement =1 cm and acceleration = 3944 cm/s²

Previous Topic: Theory of Simple Harmonic Motion

Next Topic: Numerical Problems on Maximum Velocity and Maximum Acceleration of S.H.M.

Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on Displacement, Velocity, and Acceleration of Particle Performing S.H.M.