Science > Physics > Oscillations: Simple Harmonic Motion > Simple Harmonic Motion
In this article, we shall study, the concept of linear simple harmonic motion (S.H.M.) and derive expressions for displacement, velocity, acceleration, and period of n object performing the linear simple harmonic motion.
Linear simple harmonic motion is defined as the motion of a body in which
- the body performs an oscillatory motion along its path.
- the force (or the acceleration) acting on the body is directed towards a fixed point (i.e. means position) at any instant.
- the force (or the acceleration) acting on a body is directly proportional to the displacement of the body at every instant.
e.g. the motion of heavy bob of the simple pendulum.
Examples of Linear Simple Harmonic Motion:
- The motion of the heavy bob of the pendulum.
- The motion of pivoted magnetic needle in the uniform magnetic field.
- The Motion of molecules of solid due to thermal energy.
- The motion of the needle of a sewing machine.
- The motion of prongs of tuning fork.
- The motion of medium particles, when a longitudinal or transverse wave travels through it.
Terminology of Linear Simple Harmonic Motion:
Displacement of Simple Harmonic Motion:
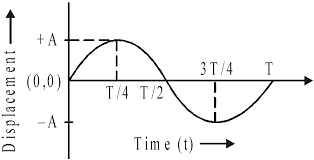
The distance of the body performing S.H.M. from its mean position is called as a displacement. It is denoted by the letter ‘x’. Its S.I. unit is metre.
Amplitude of Simple Harmonic Motion:
The maximum displacement of the body performing S.H.M. from the mean position is called as the amplitude of S.H.M. It is denoted by the letter ‘a’. Its S.I. unit is metre.
Path length or range of Simple Harmonic Motion:
The total length of the path over which the body performing linear S.H.M. moves is called the path length or range of linear S.H.M. Path length or range is twice the amplitude and in one oscillation body covers a total distance of ‘4a’. Thus, path length = 2 × amplitude
Period of Simple Harmonic Motion:
The time taken by the body performing S.H.M. to complete one oscillation is called as a period of S.H.M. It is denoted by a letter ‘T’ and its S.I. unit is second.
Frequency of Simple Harmonic Motion:
The number of oscillations performed by the body performing S.H.M in unit time (one second) is called a frequency of S.H.M. It is denoted by the letter ‘n’. Its S.I. unit is hertz (Hz).
Defining Equation of Linear Simple Harmonic Motion:
Linear simple harmonic motion is defined as the motion of a body in which
- the body performs an oscillatory motion along its path.
- the force (or the acceleration) acting on the body is directed towards a fixed point (i.e. means position) at any instant.
- the force (or the acceleration) acting on a body is directly proportional to the displacement of the body at every instant.
The force acting on the body, which is directed towards the mean position at every instant, it is called as a restoring force.
From the definition of S.H.M.
F ∝ – x
∴ F = – k x
The negative sign indicated that it is restoring force,
Where, F = restoring force, x = displacement
k is constant called force constant
This equation is known as the defining equation of linear S.H.M.
Differential Equation of Linear S.H.M.:
By definition of linear S.H.M., the force acting on a particle performing S.H.M. is given by
F = – kx ….. (1)
Where k is force per unit displacement, which is constant.
The negative sign indicates that it is a restoring force.
By Newton’s second law of motion
F = m f ….. (2)
Where m = mass of the body
f = acceleration of the body, F = restoring force acting on the body
By definition of linear acceleration,

From equations (2) and (5) we have

The equations (7) (8) and (9) (different forms) are known as differential equations of linear S.H.M. which is a second-order homogeneous differential equation.
Expression for Acceleration of a Particle Performing Linear S.H.M.:
The differential equation of S.H.M. is

Where k = Force constant, m = Mass of a body performing S.H.M.
This is an expression of an acceleration of a body performing linear S.H.M. Negative sign indicates the direction of acceleration towards the mean position or it is opposite to the direction of displacement.
Irrespective of the position of the particle performing S.H.M., the direction of acceleration is always towards the mean or equilibrium position.
Special Cases:
Case – I: When the body is at the mean position, its displacement x = 0.
f min = 0
Thus at the mean position, acceleration is minimum and i.e. zero.
Case – II: When the body is at an extreme position. The magnitude of its displacement x = a
f = ω²a
Thus at the extreme position, the magnitude of the acceleration is maximum
Expression for Velocity of a Particle Performing Linear S.H.M.:
The differential equation of S.H.M. is

Where k = Force constant, m = Mass of a body performing S.H.M.

Integrating both sides of the equation

Where C = Constant of integration, v = velocity of the body.
x = Displacement of the body.
At extreme position x = ± a and v = 0
Substituting these values in equation (1) we have

This is an expression of the velocity of the particle performing S.H.M.
Where a = amplitude of S.H.M., x = displacement of body.
The direction of velocity may be towards the mean position or away from the mean position.
Special Cases:
Case – I: When particle is at mean position i.e. x = 0

The velocity of the particle performing S.H.M. is maximum at the mean position.
Vmax = ωa
Case – II: When particle is at extreme position i.e. x = a.

The velocity of the particle performing S.H.M. is minimum and i.e. zero at the extreme position
The expression for Displacement of a Particle Performing Linear S.H.M.:
The magnitude of the velocity of the particle performing S.H.M. is given by

where a = amplitude of S.H.M., x = displacement of body.
ω = Angular velocity

Integrating both sides

Case – 1: When the particle is starting from mean position, x = 0 at t = 0.
Substituting these values in equation (1)

This is an expression for displacement of the particle performing S.H.M. and starting from mean position.
Case 2: If particle is starting from extreme position i.e. x = ± a at t = 0.
Substituting these values in equation (1)

This is is an expression for displacement of the particle performing S.H.M. and starting from an extreme position.
Case – 3: If the particle is starting from any other position than extreme or mean position. Let x = x0 when t = 0.
Substituting these values in equation (1).

This is an expression for displacement of the particle performing S.H.M. and starting from any position.
Value of α depends upon the initial conditions. If body starts from mean position α = 0. If body starts from extreme position α =± π/2.
α is called an initial phase or epoch of S.H.M. and x0 = initial displacement of the particle. It is also denoted by letter øo.
The direction of displacement is always away from the mean position.
Expression for Velocity and Acceleration of a Particle Performing S.H.M. Using Expression of Displacement:
The general equation of displacement of a particle is
x = a sin (ωt + α) ………….. (1)
The velocity of the particle can be obtained by differentiating both sides w.r.t. t,

This is an expression for the velocity of a particle performing linear S.H.M.
We can get the acceleration of the body by differentiating equation (2) again w.r.t. t.

This is an expression for the acceleration of a particle performing linear S.H.M.
Phase of S.H.M.:
Displacement of a particle performing S.H.M. is given by x = a sin (ωt + α)
where x = displacement, a = amplitude of S.H.M., = angular velocity
t = time, α = initial phase (epoch)
The quantity (ωt + α) is called as the phase of S.H.M. Phase of a body performing linear S.H.M. is defined as the state of the body w.r.t. the mean position at instant ‘t’.
When the particle is at mean position quantity (ωt + α) is zero when it is at extreme position quantity (ωt + α) is π/2. It means if particle starts moving from mean position to extreme position (ωt + α) starts increasing from zero to π/2.
When the body is at the mean position, then its phase is kπ where k = 0,1,2,3,….. and when body is at the extreme position then its phase is kπ. where k = 1,3,5,7,…..
From the value of (ωt + α), we can get an idea of the exact position and state of motion of the particle performing S.H.M.
Time Period of a Particle Performing Linear S.H.M.:
The differential equation of S.H.M. is

Where k = Force constant, m = Mass of a body performing S.H.M.

This is an expression for the time period of a particle performing linear S.H.M.
The expression for Time Period of a Particle Performing Linear S.H.M. in Terms of Force Constant:
By differential equation of S.H.M.,

Where T = Period of S.H.M.

This is an expression for the time period of S.H.M. in terms of force constant.
Uniform circular motion is a special case of linear S.H.M.:
Consider particle ‘P’ moving along a circular path with uniform angular velocity w. Let M be its projections on diameter AB of the circular path as shown in fig. The x components of displacement, velocity, and acceleration of particle P are same as x components of displacement, velocity, and acceleration of projection M respectively.
Suppose the particle P starts from the initial position with initial phaseα at time t = 0. In time t the angle between OP and x-axis is (ωt + α).

From figure,

This is an expression for displacement of particle M at time t.
The velocity of the particle M is given by

Thus the acceleration of particle M is directly proportional to the displacement of the particle and its direction is opposite to that of displacement. But this is the defining character of linear S.H.M. Hence uniform circular motion is a special case of linear S.H.M.
Restoring Force and Force Constant:
The force acting on the body performing linear S.H.M., which is directed towards the mean position (equilibrium position) at every instant, it is called as a restoring force.
From the definition of S.H.M.
F ∝ – x
∴ F = – k x
The negative sign indicated that it is restoring force,
Considering magnitude only
F = k x
k is constant called force constant
∴ k = F/x = Restoring force/displacement
S.I. Unit of force constant is N/m.
Previous Topic: Introduction to Oscillations
One reply on “Simple Harmonic Motion”
This is the best page I have all loved reading through…. because of the deep proof and highlights… Thank you so much