Simple Harmonic Progressive Wave

Science > Physics > Wave Motion > Simple Harmonic Progressive Wave

In this article, we shall study the concept of a simple harmonic progressive wave, its characteristics and its equation.

Wave in a medium may be defined as the disturbance moving through the medium without change of form. e.g. ripple in water formed due to dropping a stone in water. Wave motion is a mode of transfer of energy or a form of disturbance travelling through an elastic medium due to the repeated oscillations of the particles of the medium about their mean positions.

When a stone is dropped in water, it transfers part of its kinetic energy to the particles of water with which it comes into contact. These particles are set into vibration. Now, these vibrating particles give their energy to the neighbouring particles. Thus neighbouring particles are set into vibrations.  Thus each particle receives energy from the previous particle and passes it to the next particle. Thus wave transfer energy from one point to another.

Simple Harmonic Progressive Wave:

A simple harmonic progressive wave is a wave which continuously advances in a given direction without change of form and the particles of the medium perform simple harmonic motion about their mean position with the same amplitude and period, when the waves pass over them.

Expression for One Dimensional Simple Harmonic Progressive Wave:

Consider a simple, harmonic progressive wave travelling along the positive direction of the x-axis.  Let the vibration of the particles of the medium be parallel or perpendicular to the x-axis.  At any instant t, the displacement of the particles of the medium situated at the origin is given by,

y    =    a sin ωt

Where a is the amplitude and 2π/ω is the period of oscillation.

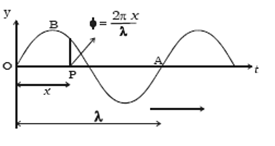
Now consider a particle of the medium situated at a point P at a distance of x from O. This particle also performs S.H.M. with the same amplitude and period, however, the disturbance from O will reach P only after some time.  In other words, the particle at P lags behind the particle at O in phase.  Hence the displacement of the particle at P at the instant t is given by

y    =    a sin (ωt – ∅).

Where, ∅ is the phase difference between O and P.

The angle ∅ depends on the distance OP. In wave motion, two particles separated by a distance λ differ in phase by 2π radians.  In other words, the path difference λ corresponds to a phase difference of 2p radians.  Therefore, the path difference x will correspond to a phase difference of ∅ = 2πx / λ. Hence, the displacement of the particle at P is given by,

This is the equation of a one dimensional simple harmonic progressive wave travelling along the positive x-axis in terms of the period of the wave.

If n is the frequency of oscillation of the particle, then T = 1/n, substituting in equation (1) we get

This is an expression for a simple harmonic progressive wave in terms of frequency of a wave.

If v is the velocity of the wave in the medium,

This is an expression for a simple harmonic progressive wave in terms of velocity of a wave. Equation (2) and (3) are two different forms of the equation of a one dimensional simple harmonic progressive wave travelling along the positive x-axis.

Equation of Simple Harmonic Progressive Wave Travelling in the Negative X – Direction:

Characteristics of a Simple Harmonic Progressive Wave:

• All particles of medium perform S.H.M. when the wave passes through the medium.
• All particles vibrate with the same amplitude.
• All particles vibrate with the same frequency.
• The propagation of the simple harmonic progressive wave is a doubly periodic phenomenon, periodic in time and periodic in space.
• Energy is transmitted through the medium.

Numerical Problems on Formation of Equation of Simple Harmonic Progressive Wave:

Example – 01:

The equation of simple harmonic progressive wave from a source is y =15 sin 100πt. Find the equation of the wave generated if it propagates along the + X-axis with a velocity of 300 m/s.

Given: Equation of source y =15 sin 100πt, Direction = + X-axis, Velocity of wave v = 300 m/s.

To Find: Equation of the wave =?

Solution:

Equation of Source wave is y =15 sin 100πt

Comparing with y =15 sin 2πnt

a = 15 m and 2πn = 100 π

∴ n = 50 Hz

Now, v = nλ

∴ λ = v/n = 300/50 = 6 m

The equation of simple harmonic progressive wave is given by

Example – 02:

Write down the equation of a transverse wave travelling along a stretched string. Given: amplitude 3 m, wavelength = 40 m and frequency = 25 Hz.

Given: Amplitude = a = 3 m, wavelength = λ = 40m, Frequency n = 25 Hz

To Find: Equation of the wave =?

Solution:

The equation of progressive wave is in the form

Example – 03:

Write down the equation of a wave moving in the positive direction of the x-axis and of amplitude 0.05 m and period 0.04 s traveling along a stretched string with a velocity 12.5 m/s.

Given: Amplitude = a = 0.05 m, Period = T = 0.04 s, Velocity = v = 12.5 m/s, Direction = + X-axis.

To Find: Equation of the wave =?

Solution:

We have v = n λ

∴  λ = v/n  = v T = 12.5 × 0.04 = 0.5 m

The equation of progressive wave is in the form

Previous Topic: Sound waves

Next Topic: Numerical Problems on Progressive waves

Science > Physics > Wave Motion > Simple Harmonic Progressive Wave