Sound Waves

Science > Physics > Wave Motion > Sound Waves

In this article, we shall study sound waves and their nature. Similarly, we shall derive the velocity of sound in air and studying the factors affecting the velocity of sound in air.

Longitudinal Nature of Sound waves:

Sound waves are the longitudinal waves. It can be explained as follows.

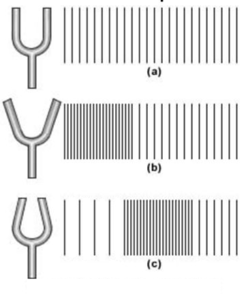
Consider vibrating tuning fork. When the prongs of the tuning fork at rest the layers of medium (air) are at normal pressure. Now let us assume that the prongs of the fork are vibrating and the prongs are parting away. During this process, the prong will push the layers of air one over other and the air in this region gets compressed. Thus in this region pressure is maximum. This region is called compression.

When the prongs return back to their normal position the pressure also becomes normal. Now, when the prongs try to come near to each other the pressure on the layers of air decreases. And layers also get parted i.e. spacing between them increases. And this condition is called a rarefaction. Again the prongs come back to their normal position and the pressure of medium again becomes normal. This process repeats continuously.

Thus alternate compression and rarefaction are formed at the same point. Thus the particles of the medium vibrate about their mean position. There is no actual migration of medium particles. Thus sound waves move forward in the form of alternate compressions and rarefactions.

Sound Waves as Audible Longitudinal Waves:

Longitudinal waves can have any possible frequencies but, a normal human ear can hear the frequencies in the range 20 Hz to 20 kHz. Therefore the longitudinal waves having frequencies in the range 20 Hz to 20 kHz are called audible longitudinal waves. These frequencies are also referred as sonic frequencies. The frequencies 20 Hz and 20kHz are known as the limits of audibility for a normal human hearing. Frequencies less than 20 Hz are called infrasonic frequencies. While the frequencies more than 20kHz are called the ultrasonic frequencies.

Newton’s Formula for Velocity of Sound waves in Air:

A change in volume of a gas carried out at a constant temperature of a gas is called isothermal change. A change in volume of a gas carried with a change in the temperature of a gas is called adiabatic change.

Newton studied the propagation of longitudinal waves through isotropic media and obtained a formula for the speed of sound in the medium

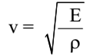
Where, E = Coefficient of elasticity of the medium

ρ = Density of the medium.

In the case of solid the elasticity, constant E is replaced by Y, The Young’s modulus of elasticity. In the case of fluids i.e. liquids and gases the elasticity constant E is replaced by K, the Bulk modulus of elasticity. Hence the formula is changed for gases as

Newton assumed the propagation of sound in air as an isothermal process. At compression, the temperature of the medium increases while the temperature at rarefaction decreases. But Newton said that there is enough time to exchange heat between the compression and rarefaction. Thus as a whole temperature of the medium remains constant and the propagation of the sound wave is an isothermal process.

For isothermal process, by Boyle’s law

PV = Constant

differentiating both sides

P dV + V. dP = 0

∴ P dV = – V. dP

∴ P = – V. dP/dV

∴ P = volumetric stress/Volumetric strain

∴ P = Bulk modulus of elasticity

For an isothermal process, the bulk constant (K) is equal to the pressure of the medium (P). Therefore, the velocity of the sound wave in the air is given by

At N.T.P. the density of air is 1.29 kg / m³. And P  = 0.76 x 13600 x 9.8 N/m².

Therefore the velocity of sound in air is given by

v = 280 m/s

But experimentally the velocity of sound is found to be 332 m/s. Thus there is a considerable difference between the actual velocity of sound in air and calculated velocity of sound in air. Hence Newton’s formula for velocity requires correction.

Laplace’s Correction to Newton’s Formula for Velocity of Sound Waves in Air:

Newton assumed the propagation of sound in air as an isothermal process. At compression, the temperature of the medium increases while the temperature at rarefaction decreases.

Laplace corrected the formula assuming the process of propagation of sound as an adiabatic process. He said that the formation of compression and rarefaction is so rapid that there is not enough time to exchange heat between compression and rarefaction. In the adiabatic process, the heat of the system remains the same. Thus no heat is lost to the surroundings and no heat is gained from the surroundings.

For adiabatic process

PV^γ = constant

Differentiating both sides

P. γV^γ-1 dV + V. dP = 0

P. γV^γ-1 dV = – V. dP

∴ γP = volumetric stress/Volumetric strain

∴ γP = Bulk modulus of elasticity = K

Where γ = Ratio of specific heats of a gas = C_P/C_V

Thus, for an adiabatic process, the bulk constant (K) is equal to γ times the pressure of the medium (P).

Therefore, the velocity of the sound wave in the air is given by

At N.T.P. the density of air is 1.29 kg / m³. And P  = 0.76 x 13600 x 9.8 N/m², and ϒ = 1.41

Therefore the velocity of sound in air is given by

v = 332 m/s

Experimentally the velocity of sound is found to be 332 m/s. the actual velocity of sound in air is almost the same as the calculated velocity of sound in air.

Numerical Problems:

Example 01:

Estimate speed of sound in air at STP using a) Newton’s formula and b) Laplace’s formula

Solution:

a) By Newton’s formula

At S.T.P. the density of air is 1.29 kg / m³. And P  = 0.76 x 13600 x 9.8 N/m².

Therefore the velocity of sound in air is given by

v = 280 m/s

b) By Laplace’s formula

At N.T.P. the density of air is 1.29 kg / m³. And P  = 0.76 x 13600 x 9.8 N/m², and ϒ = 1.41

Therefore the velocity of sound in air is given by

v = 332 m/s

Example 02:

At normal temperature and pressure 4 g of helium occupies 22.4 litres. Determine the speed of sound in helium. For helium γ = 1.67 and 1 atmospheric pressure = 10⁵ N m^-2.

Given: γ = 1.67 and P = 1 atmospheric pressure = 10⁵ N m^-2, Mass of gas = 4 g = 4 x 10^-3 kg, Volume of a gas = V = 22.4 litres = 22.4 x 10^-3 m³.

To Find: Speed of sound = v =?

Solution:

Density of gas = ρ = Mass/Volume = 4 x 10^-3 /22.4 x 10^-3 = 0.1786 kg m^-3

By Laplace’s formula

Ans: The speed of sound in helium is 967 m s^-1.

Example 03:

Calculate the speed of sound in air at atmospheric pressure taking P = 1.01 x 10⁵ N m^-2, γ = 1.40, and ρ = 1.2 kg m^-3.

Given: pressure = P = 1.01 x 10⁵ N m^-2, ratio of specific heats = γ = 1.40, and Density = ρ = 1.2 kg m^-3.

To Find: Velocity of sound = v =?

Solution:

The velocity of sound in air is given by

Ans: The speed of sound in air at atmospheric pressure is 343 m s^-1.

Example 04:

At normal temperature and pressure   1 mole (4 g) of helium occupies volume of 22.4 litres. Determine the speed of sound in helium. Given: γ for helium = 1.67, Atmospheric pressure = 10⁵ N m^-2.

Given: Mass = M = 4 g = 4 x 10^-3 kg, Volume = V = 22.4 litres = 22.4 x 10^-3 m³, γ for helium = 1.67, Atmospheric pressure = P = 10⁵ N m^-2.

To Find: Speed of sound in helium = v =?

Solution:

Density of helium = (4 x 10^-3)/(22.4 x 10^-3)

ρ = 0.1786 kg m^-3

The velocity of sound in air is given by

Ans: The speed of sound in helium is 967 m s^-1.

Previous Topic: Introduction to wave Motion

Next Topic: Simple harmonic Progressive wave

Science > Physics > Wave Motion > Sound Waves