Science > Physics > Photoelectric Effect > Thomson’s Experiment
In this article, we shall study Thomson’s experiment to find the velocity of the electron in cathode rays and the specific charge ratio of an electron.
Concept of Work Function:
When an electron tries to come out of a metal surface (atom) the remaining part of the surface (atom) acquires a positive charge. This positive charge on the remaining part of the surface pulls back the negatively charged outgoing electron. Thus certain minimum energy is to be supplied to the electron from the external agency so that the electron can escape the surface of the metal. This energy is called the work function. It is denoted by the symbol ∅. Its practical unit is eV and the S. I. unit is joule (J).
This minimum energy can be supplied to the electron by following physical processes.
- Thermionic emission: In this process, the metal is heated and sufficient thermal energy is supplied to the electrons to get emitted from the surface.
- Field Emission: By applying a very strong electric field of order 108 V/m, the emission of an electron can be achieved.
- Photoelectric Emission: When the light of a certain frequency illuminates a metal surface, the emission of an electron can be achieved.
Discovery of Electron:
J.J. Thomson discovered cathode rays during his experiment of discharge of electricity through gases at low pressure. Further studies by J.J. Thomson, W. Crooke, and J. Perin proved that the cathode rays are made up of identical negatively charged particles. These particles were called as electrons. Further J.J. Thomson in his experiments found the velocity and specific charge i.e. e/m ratio of the electron.
He proved that the specific charge or e/m ratio is the same irrespective of the material of cathode and irrespective of the nature of the gas in the discharge tube. From these observations, he concluded that electrons are fundamental particles of an atom of all substances
Effect of Electric Field on Cathode Rays Particles:
When cathode rays are passed through an electric field created by applying a potential across the plates P1 and P2, it is found that the cathode rays particles get deflected towards the positive plate. This indicates that the cathode rays particles carry a negative charge on them.
Let ‘e’ be the charge on the particle and let E’ ‘be the intensity of the electric field applied. Then the electrical force acting on the particle is given by
FE = eE
Under the action of this electric force, the particle moves in the parabolic path in the electric field. The particle leaves the electric field in the straight line in the direction tangent to the parabola at the point of leaving.
Effect of Magnetic Field on Cathode Rays Particles:
When cathode rays are passed through a magnetic field created by applying a strong magnetic field, it is found that the cathode rays particles get deflected in a circular path.
Let ‘e’ be the charge on the particle and let ‘B’ be the intensity of the magnetic field (magnetic induction) applied. Let ‘v’ be the velocity of cathode-ray particle in the field. Then the magnetic force acting on the particle is given by
FM = Bev
Under the action of this magnetic force, the particle moves in a circular path in the magnetic field. The particle leaves the magnetic field in the straight line in the direction tangent to the circular path at the point of leaving.
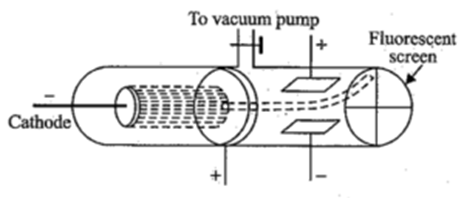
Thomson’s Experiment to Determine Specific Charge (e/m Ratio):
The velocity of the electron was first found by J.J. Thomson in 1897. Using the same experiment he found the specific charge ratio.
Construction:

The apparatus consists of a discharge tube containing gas at a very low pressure of about 0.01 mm of mercury. The discharge tube has a cathode at one end and a fluorescent screen at the other. The anode consists of a cylinder with a fine bore. The electric field can be applied between the plates P1 and P2. Plate P1 is positive and plate P2 is negative. A magnetic field can be applied perpendicular to the electric field and perpendicular to the plane of the diagram and into the plane.
Working :
Cathode emits electrons and they are collimated by cylindrical fine bore anode. The velocity of electrons depends on the potential difference between the cathode and the anode. When no field is applied. The electrons move in a straight line and form spot at B at the centre of the screen.
Effect of Electric Field:
The cathode rays are passed through only electric field created by applying a potential across the plates P1 and P2, it is found that the cathode rays particles get deflected towards the positive plate and strike the screen at A. Let e be the charge on the particle and let E be the intensity of electric field applied. Then the electrical force acting on the particle is given by
FE = eE
Under the action of this electric force, the particle moves in a parabolic path in the electric field. The particle leaves the electric field in the straight line in the direction tangent to the parabola at the point of leaving.
Effect of Magnetic Field :
The cathode rays are passed through the only magnetic field created by applying a strong magnetic field, it is found that the cathode rays particles get deflected in a circular path and strike the screen at C. Let e be the charge on the particle and let B be the intensity of magnetic field (magnetic induction) applied. Let v be the velocity of the cathode-ray particle in the field. Then the magnetic force acting on the particle is given by
FM = Bev
Under the action of this magnetic force, the particle moves in a circular path in the magnetic field. The particle leaves the magnetic field in the straight line in the direction tangent to the circular path at the point of leaving.
Determination of Velocity:
Thomson applied both the fields simultaneously and adjusted its value such that the spot remains at the centre of the screen at B. At this point
FE = FM
∴ e E = Bev
∴ v = E/B
Using this formula the velocity of the electron in the discharge tube can be determined.
Determination of e/m Ratio (Specific Charge)by Applying Electric Field Only:
If D.C. potential of V is applied between cathode and anode then the potential energy of electron entering the field is given by eV. In the field this potential energy gets converted into kinetic energy

This is the expression for determining e/m ratio
Determination of e/m Ratio (Specific Charge) by Applying Magnetic Field Only:
When the only magnetic field is applied the electron moves in a circular orbit. Necessary centripetal force is provided by the magnetic force due to the magnetic field. Let r be the radius of the circular path of an electron.

This is the expression for determining e/m ratio (Specific Charge)
Next Topic: Numerical Problems on Specific Charge