Science > Physics > Gravitation > Numerical Problems on Critical Velocity and Period of Satellite
In this article, we shall study to solve problems to calculate time period and orbital speed of satellite.
Example – 01:
Calculate the speed and period of revolution of a satellite orbiting at a height of 700 km above the earth’s surface. Assume the orbit to be circular. Take the radius of the earth as 6400 km and g at the surface of the earth to be 9.8 m/s2.
Given: height of satellite above the surface of earth = h = 700 km, Radius of earth = R = 6400 km, G = 6.67 x 10-11 N m2/kg2 ; g = 9.8 m/s2.
To Find: speed of satellite = vc = ?, Period = T = ?
Solution:
r = R + h = 6400 + 700 = 7100 km = 7.1 x 106 m,
The speed of a satellite orbiting around the earth is given by
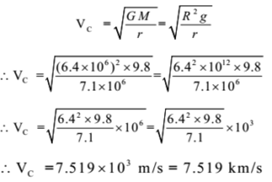
The time period of a satellite orbiting around the earth is given by
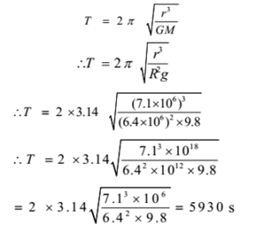
Ans: The speed of the satellite is 7.519 km/s and the period of revolution of the satellite is 5930 s.
Example – 02:
From the following data, calculate the period of revolution of the moon around the earth: Radius of earth = 6400 km; Distance of moon from the earth = 3.84 x 105 km; g = 9.8 m/s2.
Given: radius of earth = R = 6400 km = 6.4 x 108 m, radius of orbit of moon = r = 3.84 x 105 km = 3.84 x 108 m, g = 9.8 m/s2.
To find: Period of revolution of moon = T =?
Solution:
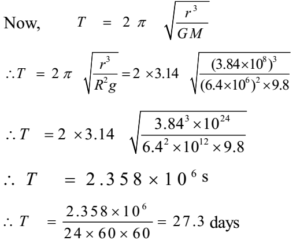
Ans: Period of the moon around the earth is 27.3 days
Example – 03:
A satellite is revolving around the earth in a circular orbit in the equatorial plane at a height of 35850 km. Find its period of revolution. What is the possible use of such a satellite? In what direction is such a satellite projected and why must it be in the equatorial plane? Given g = 9.81 m/s2; Radius of earth 6.37 x 106 m
Given: Radius of orbit of the earth =R = 6.37 x 106 m, height of satellite above the surface of the earth = h = 35850 km = 35850 x 103 m = 35.85 x 106 m, G = 6.67 10-11 N m2/kg2, g = 9.8 m/s2.
To Find: T =?
Solution:
r = R + h = 6.37 x 106 m + 35.85 x 106 m = 42.22 x 106 m

Ans: Period of the satellite is 24 hr.
Such a satellite is called geosynchronous satellite and is used for communication, broadcasting and weather forecasting. Such a satellite moves in the same direction as that of the rotation of the earth and its orbit is in the equatorial plane. If this satellite is not in the equatorial plane, it will appear to move up and down of the equatorial plane and thus it will not be stationary w.r.t. an observer on the Earth.
Example – 04:
With what velocity should a satellite be launched from a height of 600 km above the surface of the earth so as to move in a circular path?. Given: G = 6.67 x 10-11 N m2/kg2; radius of earth = 6.4 x 106 m, Mass of the earth = 5.98 x 1024 Kg.
Given: G = 6.67 x 10-11 N m2/kg2; radius of earth = R = 6.4 x 106 m = 6400 km, Mass of the earth = M = 5.98 x 1024 Kg, height of satellite above the surface of earth = 600 km, raius of orbit = 6400 + 600 = 7000 km = .7 x 106 m
To find: critical velocity = vc = ?
Solution:
The critical velocity of a satellite orbiting around the earth is given by

Ans: The velocity of the satellite for launching is 7.545 km/s.
Example – 05:
A satellite is revolving around the earth in a circular orbit at a distance of 107 m from its centre. Find the speed of the satellite. Given G = 6.67 x 10-11 N m2/kg2, Mass of the earth = M =6 x 1024 Kg,
Given: radius of orbit = 107 m, G = 6.67 x 10-11 N m2/kg2, Mass of the earth = M = 6 x 1024 Kg,
To Find: speed of satellite = vc =?
Solution:
The critical velocity of a satellite orbiting around the earth is given by

Ans: The speed of the satellite is 6.326 km/s.
Example – 06:
A body is raised to a height of 1600 km above the surface of the earth and projected horizontally with a velocity of 6 km/s. Will it revolve around the earth as a satellite? Given G = 6.67 x 10-11 N m2/kg2; radius of earth = 6.4 x 106 m, Mass of the earth = 6 x 1024 Kg.
Given: radius of earth = 6.4 x 106 m = 6400 km, Mass of the earth = 6 x 1024 Kg, height of satellite above the surface = h = 1600 km, horizontal velocity given to the satellite = v = 6 km/s, r = R + h = 6400 + 1600 = 8000 km, r = 8 x 106 m .
To find: the condition of orbiting of satellite = ?
Solution:
The critical velocity of a satellite orbiting around the earth is given by

The horizontal velocity given to satellite is 6 km/s which is less than the critical velocity of 7.073 km/s. Hence the satellite will not revolve around the earth in circular orbit but will fall back on the earth in a parabolic path.
Example – 07:
A body is raised to a height equal to the radius of the earth above the surface of the earth and projected horizontally with a velocity 7 km/s. Will it revolve around the earth as a satellite? If yes what is the nature of the orbit? Given G = 6.67 x 10-11 N m2/kg2; radius of earth = 6.4 x 106 m, Mass of the earth = 5.98 x 1024 Kg.
Given: radius of earth = 6.4 x 106 m = 6400 km, Mass of the earth = 6 x 1024 Kg, height of satellite above the surface = h = R, horizontal velocity given to the satellite = v = 7 km/s, r = R + R = 2R = 2 x 6400 = 12800 km, r = 12.8 x 106 m .
To find: the nature of the orbit of satellite =?
Solution:
The critical velocity of a satellite orbiting around the earth is given by

The horizontal velocity given to satellite is 7 km/s which is greater than the critical velocity 5.582 km/s and less than the escape velocity (11.2 km/s). Hence the satellite will revolve around the earth in an elliptical orbit.
Example – 08:
An artificial satellite is revolving around the earth in circular orbit at a height of 1000 km at a speed of 7364 m/s. Find its period of revolution if R = 6400 km
Given: Radius of earth =R = 6400 km = 6.4 x 106 m, height of satellite above the surface of the earth = h = = 1000 km = 1.0 x 106 m, radius of orbit of satellite = r = R + h = 6.4 x 106 + 1.0 x 106 m = 7.4 x 106 m, critical velocity = vc =7364 m/s..
To Find: T =?
Solution:

Ans: The period of revolution of the satellite is 1.75 hr.
Example – 09:
Moon takes 27 days to complete one revolution around the earth. Calculate its linear velocity. If the distance between the earth and the moon is 3.8 x 105 km.
Given: Radius of orbit of moon = r = 3.8 x 105 km =3.8 x 108 m, Period of moon = T = 27 days = 27 x 24 x 60 x 60 s.
To find: critical velocity = vc =?
Solution:

Ans: The linear velocity of the moon is 1.023 km/s
Example – 10:
Find the radius of the moon’s orbit around the earth assuming the orbit to be circular. Period of revolution of the moon around the earth = 27.3 days, g at the earth’s surface = 9.8 m/s2. Radius of earth = 6400 km.
Given: Radius of earth = R = 6400 km = 6.4 x 106 m, Time period = T = 27.3 days = 27.3 x 24 x 60 x 60, g = 9.8 m/s6.
To Find: radius of the orbit = r =?
Solution:


Ans: The radius of the moon’s orbit is 3.841 x 105 km
Example – 11:
Venus is orbiting around the sun in 225 days. Calculate the orbital radius and speed of the planet. Mass of sun is 2 x 1030 kg, G = 6.67 x 10-11 S.I. units.
Given: Mass of sun = M = 2 x 1030 kg, Period of venus = T = 225 days = 225 x 24 x 60 x 60 s, G = 6.67 x 10-11 S.I. units.
To Find: radius of orbit = r =? Orbital velocity = vc =?
Solution:



Ans: Orbital radius of Venus = 1.085 x 1011 m and its orbital speed = 3.506 x 104 m/s
Example – 12
An observer situated at the equator finds that a satellite is always overhead. What must be its distance from the centre of the earth? Given g at earth’s surface = 9.81 m/s2; radius of earth = 6.4 x 106 m. What is the KE of such a satellite w.r.t. an observer on earth? What must be its height above the surface of the earth?
Given: Period of Earth = T = 24 hr = 24 x 60 x 60 s, Radius of the cearth = R = 6.4 x 106 m, g = 9.8 m/s2.
To Find: radius of the orbit = r =?
Solution:


Now, r = R + h
Hence, h = r – R = 42350 – 6400 = 35950 km
Ans: Radius of the orbit of the satellite is 42350 km. The height of the satellite above the surface of the earth is 35950 km.
As the satellite is stationary w.r.t. observer, the kinetic energy of satellite w.r.t. the observer is zero.
Example – 13:
Calculate the height of the communication satellite above the surface of the earth? Given G = 6.67 x 10-11 N m2/kg2; radius of earth = 6.4 x 106 m, Mass of the earth = 6 x 1024 Kg.
Given: Period of satellite = T = 24 hr = 24 x 60 x 60 s, G = 6.67 x 10-11 N m2/kg2; radius of earth = R = 6.4 x 106 m, mass of earth = M = 6 x 1024 Kg
To Find: height of satellite above the surface of the earth = h =?
Solution:


Now, r = R + h
Hence, h = r – R = 42.35 x 106 – 6.4 x 106 = 35.92 x 106 m
h = 35920 x 106 m = 35920 km
Ans: The height of satellite above the surface of the earth is 35920 km.
Example – 14:
A satellite makes ten revolutions per day around the earth. Find its distance from the earth assuming that the radius of the earth is 6400 km and g at the earth’s surface is 9.8 m/s2.
Given: radius of earth = R = 6400 km = 6.4 x 106 m, g = 9.8 m/s2, Number of revolutions = 10 per day
To Find: radius of orbit of satellite = r =?
Solution:
T = 24/No. of revolutions per day = 24/10 = 2.4 hours


Ans: The radius of the orbit of the satellite is 9125 km
Example – 15:
A satellite is revolving around a planet in a circular orbit with a velocity of 8 km/s at a height where the acceleration due to gravity is 8 m/s2. How high is the satellite from the planet’s surface? Radius of planet = 6000 km.
Given: velocity of satellite vc = 8 km/s, R = 6400 km = 6.4 x 106 m, acceleration due to gravity at height = gh = 8 m/s2.
To Find: height of the satellite above the surface = h = ?,
The critical velocity of a satellite orbiting around the earth is given by

Now, r = R + h
Thus h = r – R = 8000 – 6400 = 1600 km
Ans: The height of the satellite above the surface of the earth is 1600 km.
Example – 16:
The critical velocity of a satellite is 5 km/s. Find the height of satellite measured from the surface of the earth given G = 6.67 x 10-11 Nm2 kg-2; R=6400 km and M = 5.98 x 1024 kg
Given: critical velocity = vc = 5 km/s, 5 x 103 m, radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 kg-2; mass of earthM = 5.98 x 1024 kg
To find: height of satellite above the surface of the earth = h = ?,
Solution:
The critical velocity of a satellite orbiting around the earth is given by

Thus h = r – R = 15950 – 6400 = 9550 km
Ans: The height of satellite above the surface of the earth is 9550 km.
Example – 17:
A satellite is revolving around a planet in a circular orbit with a velocity of 6.8 km/s. Find the height of the satellite from the planet’s surface and the period of its revolution. g = 9.8 m/s2 , R = 6400 km.
Given: velocity of satellite = vc = 6.8 km/s = 6.8 x 103 m/s, R = 6400 km = 6.4 x 106 m, g = 9.8 m/s2.
To find: height of the satellite above the surface = h =?
Solution:
The critical velocity of a satellite orbiting around the earth is given by

r = 8681 km
r = R + h
Thus h = r – R = 8681 – 6400 = 2281 km
Now,

Ans: The height of the satellite above the surface of the earth is 2281 km and the period of the satellite is 8017 s
Previous Topic: Theory of Critical Velocity and Period of Satellite
Next Topic: More Problems on Critical Velocity and Period of Satellite