Formation of Stationary waves

Science > Physics > Stationary Waves > Introduction to Stationary Waves

Waves are classified as progressive waves and stationary waves. In this article, we shall study the meaning of stationary waves, their formation, and their characteristics.

Mechanical waves:

The waves which require an elastic medium for their propagation is called mechanical waves e.g. sound waves.

Progressive Wave:

The wave advancing in the given direction continuously is called a progressive wave e.g. sound waves. In an unbounded (infinite)) medium, the progressive wave travels in a given direction continuously until it gets dissipated.

Characteristics of Progressive Waves:

• They are produced when a disturbance is created in an elastic medium.
• They continuously travel away from the source.
• They transfer energy through the medium.
• All the particles of the medium perform SHM with the same amplitude.
• Every particle of the medium is set into vibrations.
• Different particles have got different phases at a given instant.
• Equation of the wave is

y = a sinn2π(t/T – x/ λ )

Characteristics of Beats:

• They are produced due to interference between the progressive waves which need not be traveling in opposite directions.
• Interfering waves must have slightly different frequencies.
• At a given point, amplitude changes with time.
• At a given point, the intensity of sound varies from a maximum to a minimum.
• Waxing and waning of the sound of resulting intensity are produced.
• The resultant wave travels in the forward direction.

Reflection of a Wave:

In an unbounded (infinite) medium the wave travels in a given direction continuously until its energy is dissipated. In bounded (finite) medium, the wave arrives at a boundary of the medium and reflects back. Production of an echo is an example of the reflection of sound waves. Wave when reflected from the boundary of a rigid surface, has a phase difference of π radian and when reflected from the unbounded medium, has a phase difference of zero radians.

Stationary Waves:

When two, identical, progressive waves of equal amplitudes and equal wavelengths and traveling in the same medium, along the same straight line, but in opposite directions, interfere, then the wave formed is called a standing wave or a stationary wave.

As the velocities of the two interfering waves are equal and opposite, the resultant wave does not travel either forward or backward and hence no energy is transported through the medium. Such a wave is called a stationary wave.

Explanation of Formation of Stationary Waves:

Let the two interfering waves be represented by the equations.

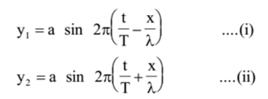
They are of the same amplitude ‘a’ and have the same period ‘T’ and are traveling with the same velocity ‘v’ along x-axis but in opposite directions. When they superimpose, the resultant displacement is given by

y = y₁ + y₂

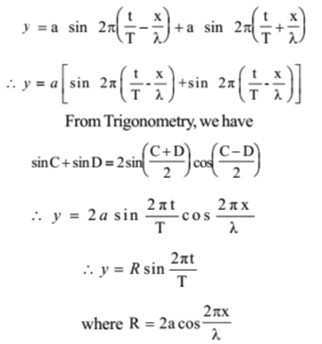
Thus the resultant motion is also S. H. M. of the same period. The absence of ± x/λ in the phase term indicates that the wave is traveling neither forwards nor backward.  The amplitude R is not constant but varies periodically with the distance x.  We call the motion wave motion because we can think of it as a superposition of two waves traveling in opposite directions.

Case – I (Maxima)

Case- II (Minima)

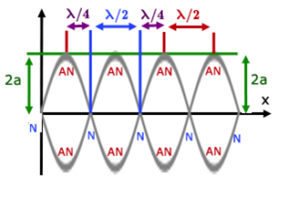
The overall appearance of the wave is therefore as shown in the figure.

The points at which the amplitude becomes zero are the nodes. The points at which the amplitude becomes maximum are the antinodes. The distance between the two successive nodes or two successive antinodes is λ/2.  Also, an antinode is situated exactly midway between two adjacent nodes and vice-versa.  In other words, the distance between a node and an adjacent antinode is λ/4. Also, we can conclude that the nodes and antinodes are alternate and equally spaced.

Displacement Nodes or Nodes:

When a stationary wave passes through a medium, the points of the medium at which the displacement is minimum i.e. zero thus amplitude becomes zero are called displacement nodes simply nodes. The displacement nodes are pressure antinodes. At these points pressure is maximum.

Displacement Antinodes or Antinodes:

When a stationary wave passes through a medium, the points of the medium at which the displacement is maximum i.e. amplitude is maximum are called displacement antinodes or simply antinodes. The displacement antinodes are pressure nodes. At these points pressure is minimum.

Characteristics of Stationary Waves:

• They are produced due to the interference of two identical progressive waves traveling along the same path but in opposite directions.
• They move neither forward nor backward.
• In a stationary wave, the energy is not transported from one point to another.
• The particles of the medium perform S. H. M. of the same period but the amplitude of the oscillations varies periodically in space.
• There are some particles of the medium which do not at all vibrate i.e. their amplitude is zero.  These are called nodes. Some particles vibrate with maximum amplitude and are called antinodes.
• All the particles in the same loop have the same phase at a given instant.
• Equation of the wave is

• The distance between two successive antinodes, or two successive nodes is constant and equal to l/2.
• The distance between a node and the adjacent antinodes is λ/4.
• There is no progressive change of phase from particle to particle.  In fact, all the particles in any one segment or loop vibrate in the same phase, while particles in any two adjacent segments are in the opposite phase.
• Stationary waves can be produced by the interference of either longitudinal or transverse waves.

Next Topic: Vibrations of String

Science > Physics > Stationary Waves > Introduction to Stationary Waves