Stefan’s Law of Radiation

Science > Physics > Radiation > Stefan’s Law of Radiation

In this article, we shall study Stefan’s law of radiation, Newton’s law of cooling, derivation of Newton’s law of cooling from Stefan’s law and to calculate the temperature of the solar surface.

Stefan’s Law:

Statement:

The heat energy radiated per unit time per unit area of a perfectly black body is directly proportional to the fourth power of its absolute temperature.

Explanation: 

Let E_b, the heat radiated per unit time per unit area of a perfectly black body whose absolute temperature is T.

So by Stefan’s Law,

E_b ∝ T⁴

E_b   = σ T⁴

Where σ is a constant known as Stefan’s constant.

The value of σ in S.I. system is 5.67 × 10^-8 Jm^-2 K^-4s^-1 or 5.67 x 10^-8 Wm^-2 K^-4. The value of σ in c.g.s system is 5.67 × 10^-5 erg cm^-2 C°^-4s^-1. Dimensions of σ are [M¹L⁰T^-3K^-4]

Expression for the Rate of Loss of Heat to the Surrounding:

Let T be the absolute temperature of a perfectly black body. Let T_o be the absolute temperature of the surrounding.

So by Stefan’s Law,

Heat radiated per unit time per unit area of a perfectly black body   = σ T⁴

Let A be the surface area of the perfectly black body. Then,

Heat lost by the body per   unit   time = A σ T⁴

Where σ is a constant known as Stefan’s constant.

Heat   received  from the surrounding per unit time = A σ T_o⁴

The net rate of loss of heat = A σ T⁴ – A σ T_o⁴

= A σ(  T⁴ – T_o⁴)

This is an expression for the rate of loss of heat to the surrounding.

Newton’s Law of Cooling:

Statement:

The rate of loss of heat by a body is directly proportional to its excess temperature over that of the surroundings provided that this excess is small.

Explanation: 

Let θ and θ_o, be the temperature of a body and its surroundings respectively. Let dQ / dt be the rate of loss of heat, So from Newton’s Law of Cooling,

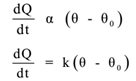
Where k is a constant.

Alternate Statement:

By Newton’s law of cooling, mathematically

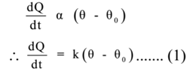
Where, θ and θ_o, are the temperature of the body and its surroundings respectively and

dQ / dt is the rate of loss of heat. K is constant.

Let ‘m’ be the mass of the body, c be its specific heat.

Thus, the rate of fall of a temperature of a body is directly proportional to its excess temperature over that of the surroundings.

Derivation of Newton’s Law of Cooling from Stefan’s Law:

Let us consider a body whose surface area is A having absolute temperature T and kept in the surrounding having absolute temperature T_o.  Let e be the emissivity (or coefficient of emission) of the surface of the body.

Let (T  -T_o) =  x,  where  x  is Small.

∴ T   =  T_o  +    x.

Let dQ/ dt be the rate of loss of heat by the body. We know that

E / E_b = e

∴ E = e E_b

Where E & E_b, are the emissive powers of the body and perfectly black body respectively.

Using Stefan’s Law we know that for a perfectly black body rate of loss of heat = Aσ(  T⁴   –  T_o⁴ )

Therefore, for a given body,

As x /T_o is small so higher powers of x /T_o will be very small and hence those terms can be neglected.

This is Newton’s Law of cooling i.e. the rate of loss of heat of a body is directly proportional to its excess temperature over the surroundings provided the excess is small. Thus Newton’s Law of Cooling is derived (or deduced) from Stefan’s Law.

Limitations of Newton’s Law of Cooling:

• This law is applicable when the excess temperature of a body over the surroundings is very small (about 40^oC)
• When the body is cooling the temperature of the surrounding is assumed to be constant. Which is not true.
• The law is applicable for higher temperature using forced convection.

Solar Constant:

The solar constant is the rate at which solar radiant energy is intercepted by the earth per unit area at the outer limits of the earth’s atmosphere at the earth-sun mean distance.

The solar constant, S = 1353 W/m².

Calculation of Surface Temperature of the Sun:

The central portion of the sun is very hot. It has a temperature of 10⁷ K. It can be estimated using concepts of nuclear reactions.

The outer surface of the sun is comparatively cooler this region is called the photosphere. Its temperature can be estimated using solar constant.

Let T be the absolute temperature of the surface of the sun. Let Rs be its radius. By Stefan’s law, the total power radiated per second is given by

Where σ = Stefan’s constant

Let r be the earth-sun mean distance. r = 1.496 × 10¹¹ m,

Now the energy radiated by the sun is distributed over a sphere of surface area 4πr². By definition of the solar constant

Previous Topic: Concept of Black Body

Next Topic: Numerical Problems on Newton’s Law of Cooling

Science > Physics > Radiation > Stefan’s Law of Radiation