Science > Physics > Photoelectric Effect >Numerical Problems on Einstein’s Photoelectric Equation
In this article. we are going to study to calculate the stopping potential and maximum kinetic energy of the photoelectron using Einstein’s photoelectric equation.
Example 01:
A metal whose work function is 4.2 eV is irradiated by radiation whose wavelength is 2000 A. Find the maximum kinetic energy emitted electron.
Given: Work function Φ = 4.2 eV = 4.2 x 1.6 x 10-19 J = 6.72 x 10-19 J, wavelength of radiation = l = 2000 A = 2000 x 10-10 m = 2 x 10-7 m, Planck’s constant = 6.63 x 10-34 Js.
To find: maximum kinetic energy = K.E.max = ?
Solution:
By Einstein’s photoelectric equation
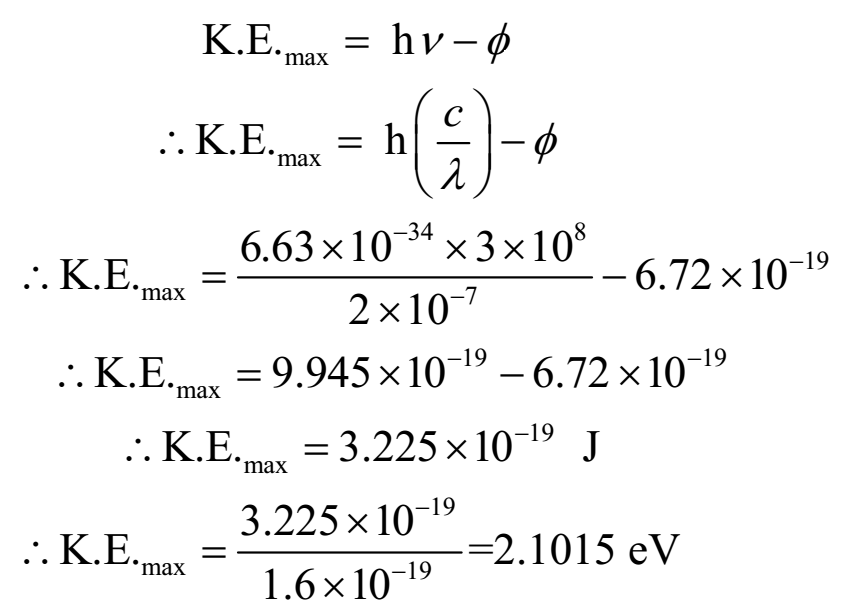
Ans: Thus maximum kinetic energy of emitted electron is 2.015 eV
Example 02:
If photoelectrons are to be emitted from potassium surface with speed of 6 x 105 m/s, what frequency of radiation must be used? Threshold frequency for potassium is 4.22 x 1014 Hz.
Given: speed of electron = v = 6 x 105 m/s, Threshold frequency = νo = 4.22 x 1014 Hz. Planck’s constant = h = 6.63 x 10-34 Js.
To find: Frequency of incident radiation = n = ?
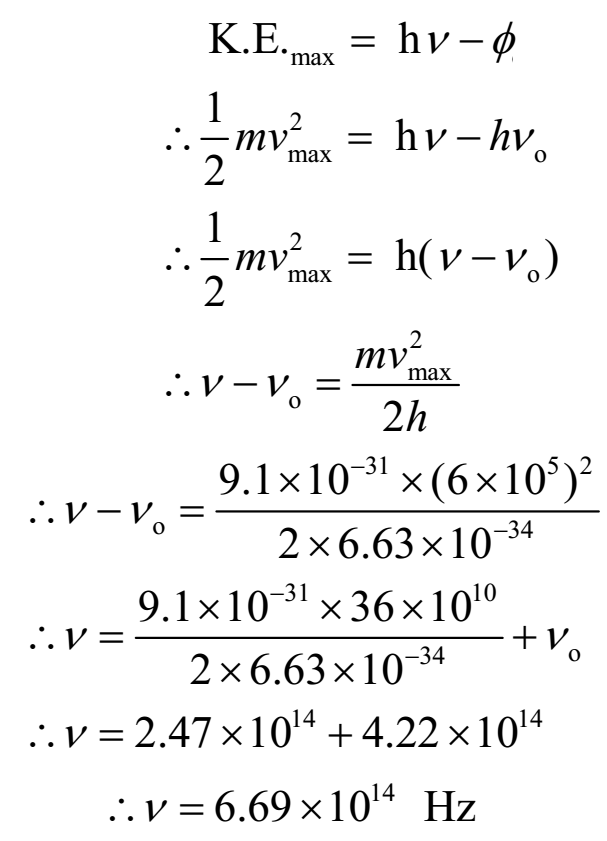
Ans: Frequency of incident radiation is 6.69 x 1014 Hz.
Example – 03:
When radiation of certain wavelength shines on the cathode of the photoelectric cell, the photocurrent produced can be reduced to zero by applying stopping potential of 2.63 V. If the work function of the photo emitter is 4 eV, find the wavelengths of radiation.
Given: Stopping potential = Vs = 2.63 V, work function = Φ = 4 eV = 4 x 1.6 x 10-19 J = 6.4 x 10-19 J, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: Wavelength of radiation = λ =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – Φ
But K.E. max = eVs
eVs = hc/λ – Φ
∴ (1.6 x 10-19) x (2.63) = (6.63 x 10-34) (3 x 108)/λ – 6.4 x 10-19
∴ 4.21 x 10-19 + 6.4 x 10-19 = (19.89 x 10-26)/λ
∴ 10.61 x 10-19 = (19.89 x 10-26)/λ
∴ λ = (19.89 x 10-26) / (10.61 x 10-19)
∴ λ = 1.871 x 10-7 = 1871x 10-10 m = 1871 Å
Ans: The wavelength of radiation is 1871 Å
Example – 04:
Radiation of wavelength 3000 A falls on a photoelectric surface for which work function is 1.6 eV. What is the stopping potential for emitted electron?
Given: Wavelength of radiation = λ = 3000 Å = 3000 x 10-10 m, work function = Φ = 1.6 eV = 1.6 x 1.6 x 10-19 J = 2.56 x 10-19 J, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: Stopping potential = Vs =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – Φ
But K.E. max = eVs
eVs = hc/λ – Φ
∴ (1.6 x 10-19) x Vs = (6.63 x 10-34) (3 x 108)/(3000 x 10-10) – 2.56 x 10-19
∴ (1.6 x 10-19) x Vs = 6.63 x 10-19 – 2.56 x 10-19
∴ Vs = 4.07 x 10-19
∴ Vs = (4.07 x 10-19)/(1.6 x 10-19)
∴ Vs = 2.54 V
Ans: The stopping potential is 2.54 V.
Example – 05:
When radiation of certain wavelength shines on the cathode of the photoelectric cell, the photocurrent produced can be reduced to zero by applying stopping potential of 3 V. If the work function of the photo emitter is 3.63 eV, find the frequency of radiation.
Given: Stopping potential = Vs = 3 V, work function = Φ = 3.63 eV = 3.63 x 1.6 x 10-19 J, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: frequency of radiation = ν =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – Φ
But K.E. max = eVs
eVs = hν – Φ
∴ (1.6 x 10-19) x (3) = (6.63 x 10-34) ν – 3.63 x 1.6 x 10-19
∴ 4.8 x 10-19 = (6.63 x 10-34) ν – 5.808 x 10-19
∴ 4.8 x 10-19 + 5.808 x 10-19 = (6.63 x 10-34) ν
∴ 10.608 x 10-19 = (6.63 x 10-34) ν
∴ ν = (10.61 x 10-19)/(6.63 x 10-34)
∴ ν = 1.6 x 1015 Hz
Ans: The frequency of radiation is 1.6 x 1015 Hz
Example – 06:
Photoelectrons emitted by a surface have maximum kinetic energy of 4 x 10-19 J. What is the stopping potential for photo emission from the surface for the incident radiation?
Given: Maximum kinetic energy of photoelectron = K.E. max = 4 x 10-19 J, Charge on electron = e = 1.6 x 10-19 C.
To Find: frequency of radiation = ν =?
Solution:
K.E. max = eVs
Vs = K.E. max/e
∴ Vs = (4 x 10-19)/(1.6 x 10-19) = 2.5 V
Ans: The stopping potential = 2.5 V
Example – 07:
Light of wavelength 2000 Å is incident on the cathode of a photocell. The current in the photocell is reduced to zero by stopping potential of 2 V. Find the threshold wavelength of the material of cathode.
Given: Stopping potential = Vs = 2 V, wavelength of incident light = λ = 2000 Å = 2000 x 10-10 m, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: frequency of radiation = ν =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – Φ
But K.E. max = eVs
eVs = hc/λ – Φ
∴ (1.6 x 10-19) x 2 = (6.63 x 10-34) (3 x 108)/(2000 x 10-10)- Φ
∴3.2 x 10-19 = 9.945 x 10-19 – Φ
∴ Φ = 9.945 x 10-19 – 3.2 x 10-19 = 6.745 x 10-19 J
We have Φ = h νo = hc/λo
∴ λo = hc/Φ =(6.63 x 10-34) x (3 x 108) / ( 6.745 x 10-19) = 2.949 x 10-7 m
∴ λo= 2949 x 10-10 m = 2949 Å
Ans: The threshold wavelength is 2949 Å
Example – 08:
Photoelectrons are ejected from metal surface when radiation of wavelength 160 nm is incident on the surface. Find stopping potential of emitted electrons if the limiting wavelength is 240 nm for photoelectric emission from the surface.
Given: Stopping potential = Vs = 2 V, wavelength of incident light = λ = 160 nm = 160 x 10-9 m, Threshold wavelength = λo = 240 nm = 240 x 10-9 m, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: Stopping potential = Vs =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – hc/λo
But K.E. max = eVs
∴ eVs = hc/λ – hc/λo
∴ eVs = hc(1/λ – 1/λo)
∴ (1.6 x 10-19) x Vs = (6.63 x 10-34)(3 x 108)(1/(160 x 10-9) – 1/(240 x 10-9))
∴ (1.6 x 10-19) x Vs = (6.63 x 10-34)(3 x 108)x 109 x (1/160 – 1/240 )
∴ (1.6 x 10-19) x Vs = 19.89 x 10-17 x (240 -160)/(160 x240 )
∴ (1.6 x 10-19) x Vs = 19.89 x 10-17 x 80/(160 x240 )
∴ (1.6 x 10-19) x Vs = 4.143 x 10-19
∴ Vs = 4.143 x 10-19/ (1.6 x 10-19) = 2.59 eV
Ans: the stopping potential is 2.59 eV
Example – 09:
Calculate the change in stopping potential when the wavelength of light incident on photoelectric surface is reduced from 4000 Å to 3600 Å.
Given: Initial wavelength = λ1 = 4000 Å = 4000 x 10-10 m = 4 x 10-7 m, Final wavelength = λ2 = 3600 Å = 3600 x 10-10 m = 3.6 x 10-7 m, speed of light = c = 3 x 108 m/s, Planck’s constant = h = 6.63 x 10-34 Js, Charge on electron = e = 1.6 x 10-19 C.
To Find: Stopping potential = Vs =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ = hc/λ – Φ
But K.E. max = eVs
∴ eVs1 = hc/λ1 – Φ ……….. (1)
∴ eVs2 = hc/λ2 – Φ ……….. (2)
Subtracting equation (1) from (2)
∴ eVs2 – eVs1 = (hc/λ2 – Φ) – (hc/λ1 – Φ)
∴ e (Vs2 – Vs1) = hc/λ2 – hc/λ1
∴ e (Vs2 – Vs1) = hc(1/λ2 – 1/λ12)
∴ (1.6 x 10-19) (Vs2 – Vs1) = (6.63 x 10-34) (3 x 108)(1/(3.6x 10-7) – 1/(4 x 10-7))
∴ (1.6 x 10-19) (Vs2 – Vs1) = (6.63 x 10-34) (3 x 108) x 107 x (1/3.6 – 1/4)
∴ (1.6 x 10-19) (Vs2 – Vs1) = 19.89 x 10-19 x (4 – 3.6)/1(3.6 x 1/4)
∴ (1.6 x 10-19) (Vs2 – Vs1) = 19.89 x 10-19 x 0.4/1(3.6 x 1/4)
∴ (1.6 x 10-19) (Vs2 – Vs1) = 5.525 x 10-20
∴ (Vs2 – Vs1) = 5.525 x 10-20/(1.6 x 10-19) = 0.3453 V
Ans: the change in stopping potential is 0.3453 eV
Example – 10:
When light of frequency 2.2 x 1015 Hz is incident on a metal surface, photoelectric current can be stopped by a retarding potential of 6.6 V. For light of frequency 4.6 x 1015 Hz the reverse potential is 16.5 V. Find h
Given: Initial frequency = ν1 = 2.2 x 1015 Hz, initial stopping potential = Vs1 =6.6 V, Final frequency = ν2 = 4.6 x 1015 Hz, Final stopping potential = Vs2 = 16.5 V, Charge on electron = e = 1.6 x 10-19 C.
To Find: Planck’s constant = h =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ
But K.E. max = eVs
∴ eVs = hν – Φ
∴ eVs1 = hc/λ1 – Φ ……….. (1)
∴ eVs2 = hc/λ2 – Φ ……….. (2)
Subtracting equation (1) from (2)
∴ eVs2 – eVs1 = (hν2 – Φ) – (hν1 – Φ)
∴ e (Vs2 – Vs1) = hν2 – hν1
∴ e (Vs2 – Vs1) = h(ν2 – ν2)
∴ (1.6 x 10-19) (16.5 – 6.6) = h (4.6 x 1015 – 2.2 x 1015)
∴ 1.6 x 10-19 x 9.9 = h (2.4 x 1015)
∴ h = (1.6 x 10-19 x 9.9) / (2.4 x 1015)
∴ h = 6.6 x 10-34 Js
Ans: the value of Planck’s constant is 6.6 x 10-34 Js
Example – 11:
When light of frequency 2 x 1015 Hz is incident on a metal surface, photoelectric current can be stopped by a retarding potential of 6 V. For light of frequency 1015 Hz the reverse potential is 2 V. Find Planck’s constant, work function and threshold frequency.
Given: Initial frequency = ν1 = 2 x 1015 Hz, initial stopping potential = Vs1 = 6 V, Final frequency = ν2 = 1015 Hz, Final stopping potential = Vs2 = 2 V, speed of light = c = 3 x 108 m/s, Charge on electron = e = 1.6 x 10-19 C.
To Find: Planck’s constant = h =?
Solution:
By Einstein’s photoelectric equation
K.E. max = hν – Φ
But K.E. max = eVs
∴ eVs = hν – Φ
∴ eVs1 = hν1 – Φ ……….. (1)
∴ eVs2 = hν2 – Φ ……….. (2)
Subtracting equation (2) from (1)
∴ eVs1 – eVs2 = (hν1 – Φ) – (hν2 – Φ)
∴ e (Vs1 – Vs2) = hν1 – hν2
∴ e (Vs1 – Vs2) = h(ν1 – ν2)
∴ (1.6 x 10-19) (6 – 2) = h (2 x 1015 – 1015)
∴ 1.6 x 10-19 x 4 = h (1 x 1015)
∴ h = (1.6 x 10-19 x 4)/1 x 1015)
∴ h = 6.4 x 10-34 Js
From equation (1) we have
eVs1 = hν1 – Φ
∴ 1.6 x 10-19 x 6 = 6.4 x 10-34 x 2 x 1015 – Φ
∴ 9.6 x 10-19 = 12.8 x 10-19 – Φ
∴ Φ = 12.8 x 10-19 – 9.6 x 10-19
∴ Φ = 3.2 x 10-19 J
∴ Φ = (3.2 x 10-19) / (1.6 x 10-19) = 2 eV
Φ = hνo
νo = Φ /h = (3.2 x 10-19 )/(6.4 x 10-34) = 5 x 1014 Hz
Ans: the value of Planck’s constant is 6.4 x 10-34 Js,
work function = 2 eV and Threshold frequency = 5 x 1014 Hz
Previous Topic: Einstein’s Photoelectric Equation (Theory)
Next Topic: Applications of Photoelectric Effect
9 replies on “Numerical Problems on Einstein’s Photoelectric Equation”
perfect have real learnt a lot
It was a great experience
thanks, i understand to calculate the stopping potential very well from your numericals
oh gosh! it was so interesting, i like it
Thanks, i understand to calculate the stopping voltage very well from your examples . thank you 💙💙
Thanks; I have learn a lot from your solutions. May God bless
I really understood your question and it’s helping
This is awesome faa… Thanks for every time
I really understood your question and it’s helping