Expansion of Solids

Science > Physics > Thermal Properties of Matter and Thermodynamics > Expansion of Solids

Whenever there is an increase in the dimensions of a body due to heating, then the body is said to be expanded and the phenomenon is known as expansion of solids. Solids undergo three types of expansions a) Linear (Longitudinal) expansions, b) Superficial expansions (Arial) and c) Cubical expansions (Volumetric)

LIST OF SUB-TOPICS:

• Linear Expansion of Solids
• Characteristics of Coefficient of Linear Expansion
• Factors Influencing the Coefficient of Linear Expansion
• Coefficient of Linear Expansion for Different Materials
• Superficial Expansion of Solids
• Cubical Expansion of Solids
• Relation Between α and β
• Relation Between α and γ
• Relation Between α, β and γ
• Molecular Explanation of Expansion of Solids:

Linear Expansion of Solid:

Linear expansion or longitudinal expansion refers to the increase in length of a solid material when its temperature rises. This phenomenon occurs due to the increased thermal energy within the material, causing its constituent particles to vibrate more vigorously, thereby increasing the average distance between them.

Expression for the Coefficient of Linear Expansion of Solids:

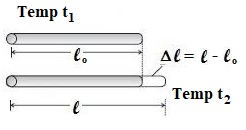
Consider a metal rod of length ‘l₀’ at temperature 0 °C. Let the rod be heated to some higher temperature say t °C. Let ‘l’ be the length of the rod at temperature t °C.

∴ Change in temperature = t₂ – t₁ = t – 0 = t

and Change in length = l – l₀

Experimentally it is found that the change in length ( l – l₀) is

Directly proportional to the original length (l₀)

l – l₀   ∝  l₀   ………………. (1)

Directly proportional to the change in temperature (t)

l – l₀   ∝  t …………… (1)

Dependent upon the material of the rod.

From equation (1) and (2)

l – l₀   ∝  l₀ t

∴   l – l₀   =  α l₀ t    …………… (3)

Where ‘α’ is a constant called a coefficient of linear expansion

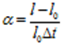
This is an expression for the coefficient of linear expansion of a solid.

The coefficient of linear-expansion is defined as the increase in length per unit original length at 0⁰c per unit rise in temperature.

From equation (3) we get

∴   l   = l₀ + α l₀ t

∴   l   = l₀ (1 + α t) ………….. (4)

This is an expression for the length of rod at t °C

Note: The magnitude of the coefficient of linear expansion is so small that it is not necessary to take the initial temperature at 0 °C.

Consider a metal rod of length ‘l₁’ at temperature t₁0 °C. Let the rod be heated to some higher temperature say t °C. Let ‘l₂’ be the length of the rod at temperature t₂ °C. Let l₀’ be the length of the rod at the temperature of 0 °C. Let α be the coefficient of linear expansion, then we have

l₁ = l₀ (1 + α t₁) ………….. (2)

l₂ = l₀ (1 + α t₂) ………….. (2)

Dividing equation (2) by (1) we get

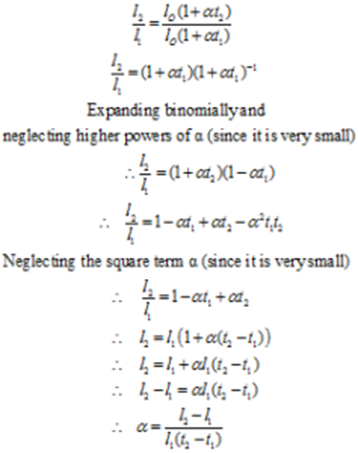
The coefficient of linear expansion is different for different material

Back to List of Sub-Topics

Characteristics of Coefficient of Linear Expansion:

The coefficient of linear expansion is a material property that describes how much a material will expand or contract in length for a given change in temperature. The change in length of the material is directly proportional to the original length, the change in temperature, and the coefficient of linear expansion. Key characteristics of the coefficient of linear expansion are as follows:

• Material Specific: The coefficient of linear expansion varies from one material to another. Different materials have different rates of expansion or contraction for the same change in temperature.
• Temperature Dependence: While the coefficient of linear expansion is often treated as a constant over a small temperature range, it can vary slightly with temperature. However, for most materials and within normal temperature ranges, this variation is negligible for practical purposes. Coefficient of linear expansion generally decreases with the increase in temperature.
• Directionality: The coefficient of linear expansion is directional and applies along a specific axis of the material. For instance, in an anisotropic material like wood, the coefficient of linear expansion can be different along different axes.
• Units: The coefficient of linear expansion is typically expressed in units of per degree Celsius or per Kelvin
• Thermal Stress Inducer: Differences in the coefficients of linear expansion between materials can lead to thermal stresses when they are bonded together. These stresses can cause mechanical failure or deformation in structures or devices.
• Measurement: Coefficients of linear expansion can be determined experimentally through techniques such as dilatometry, which involves measuring the change in length of a material for known changes in temperature.

Understanding the coefficient of linear expansion is crucial in engineering and construction to design structures that can accommodate thermal expansion and contraction without causing damage or failure. The coefficient of linear expansion is an essential parameter for understanding how materials respond to temperature changes and for designing systems that can withstand such thermal effects.

Back to List of Sub-Topics

Factors Influencing the Coefficient of Linear Expansion:

The coefficient of linear expansion of a material is influenced by several factors, including:

• Chemical Composition: The chemical composition of a material significantly affects its coefficient of linear expansion. Different materials have different atomic and molecular structures, which lead to variations in their expansion behaviour.
• Crystal Structure: The crystal structure of a material can influence its coefficient of linear expansion. For example, crystalline materials may have different expansion characteristics along different crystallographic directions.
• Temperature Range: The coefficient of linear expansion can vary depending on the temperature range over which it is measured. In some materials, the coefficient of linear expansion may change with temperature, especially at extreme temperatures.
• Impurities and Alloying Elements: The presence of impurities or alloying elements in a material can alter its coefficient of linear expansion. Alloying elements may introduce lattice distortions or changes in the bonding behaviour, affecting the material’s expansion properties.
• Phase Transitions: Phase transitions, such as melting or solid-state transformations, can affect the coefficient of linear expansion. Different phases of a material may exhibit different expansion behaviours.
• Anisotropy: Some materials exhibit anisotropic behaviour, meaning their properties vary depending on the direction of measurement. Anisotropy can result from the material’s crystal structure or processing methods and can lead to different coefficients of linear expansion along different axes.
• Microstructure: The microstructure of a material, including factors such as grain size, grain boundaries, and defects, can influence its coefficient of linear expansion. Grain boundaries and defects may act as obstacles to atomic movement and affect the material’s expansion behaviour.
• External Stress and Strain: The coefficient of linear expansion may change under the influence of external stress or strain. Mechanical deformation or stress can alter the material’s atomic arrangement and affect its expansion properties.
• Environmental Conditions: Environmental factors such as humidity, pressure, and the presence of reactive gases can influence the coefficient of linear expansion. Changes in these environmental conditions may affect the material’s structure and expansion behaviour.

Understanding the factors that influence the coefficient of linear expansion is crucial for predicting and engineering the thermal behaviour of materials in various applications, including construction, manufacturing, and thermal management systems.

Back to List of Sub-Topics

Coefficient of Linear Expansion for Different Materials:

Metals	Coefficient of linear expansion at 20 °C ()
Aluminium	23.1 x 10-6 K-1
Benzocyclobutene	42 x 10-6 K-1
Brass	19 x 10-6 K-1
Carbon steel	10.8 x 10-6 K-1
Concrete	12 x 10-6 K-1
Copper	17 x 10-6 K-1
Diamond	1 x 10-6 K-1
Ethanol	250 x 10-6 K-1
Gallium(III) Arsenide	5.8 x 10-6 K-1
Gasoline	317 x 10-6 K-1
Gold	14 x 10-6 K-1
Ice	51 x 10-6 K-1
Iron	11.8 x 10-6 K-1
Lead	29 x 10-6 K-1
Magnesium	26 x 10-6 K-1
Mercury	61 x 10-6 K-1
Nickel	13 x 10-6 K-1
Platinum	9 x 10-6 K-1
Water	69 x 10-6 K-1
Silicon	2.56 x 10-6 K-1
Silver	18 x 10-6 K-1

Back to List of Sub-Topics

Superficial Expansion of Solids:

Whenever there is an increase in the area of a solid body due to heating then the expansion is called superficial or Arial expansion.

Expression for the Coefficient of Superficial Expansion of Solids:

Consider a thin metal plate of area ‘A₀’ at temperature 0 °C. Let the plate be heated to some higher temperature say t °C. Let ‘A’ be the area of the plate at temperature t °C.

∴ Change in temperature = t₂ – t₁ = t – 0 = t

and Change in area = A- A₀

Experimentally it is found that the change in the area (A- A₀) is

Directly proportional to the original area (A₀)

A – A₀   ∝ A₀   ………………. (1)

Directly proportional to the change in temperature (t)

A – A₀   ∝ t ………….. (1)

Dependent upon the material of the plate

From equation (1) and (2)

A – A₀   ∝ A₀ t

∴   A – A₀   = β A₀ t    …………… (3)

Where ‘β’ is a constant called a coefficient of superficial expansion

This is an expression for the coefficient of superficial expansion of a solid.

The coefficient of superficial expansion is defined as the increase in area per unit original area at 0⁰c per unit rise in temperature.

From equation (3) we get

∴ A   = A₀ + β A₀ t

∴ A   = A₀ (1 + β t) ………….. (4)

This is an expression for the area of the plate at t °C

Note: The magnitude of the coefficient of superficial expansion is so small that it is not necessary to take the initial temperature as 0 °C.

Consider a thin metal plate of area ‘A₁’ at temperature t₁0 °C. Let the plate be heated to some higher temperature say t °C. Let ‘A₂’ be the area of the plate at temperature t₂ °C. Let ‘A₀’ be the area of the plate at a temperature of 0 °C. Let β be the coefficient of superficial expansion, then we have

A₁ = A₀ (1 +    β t₁) ………….. (2)

A₂ = A₀ (1 +    β t₂) ………….. (2)

Dividing equation (2) by (1) we get

The coefficient of superficial expansion is different for different material

Back to List of Sub-Topics

Cubical Expansion of Solids:

Whenever there is an increase in the volume of the body due to heating the expansion is called cubical or volumetric expansion.

Expression for the Coefficient of Cubical Expansion of Solids:

Consider a solid body of volume ‘V₀’ at temperature 0 °C. Let the body be heated to some higher temperature say t °C. Let ‘V’ be the volume of the body at temperature t °C.

∴ Change in temperature = t₂ – t₁ = t – 0 = t

and Change in volume = V – V₀

Experimentally it is found that the change in the volume (V – V₀) is

Directly proportional to the original volume (V₀)

V – V₀  ∝  V₀   ………………. (1)

Directly proportional to the change in temperature (t)

V – V₀  ∝  t………………. (1)

Dependent upon the material of the body.

From equation (1) and (2)

V – V₀  ∝  V₀ t

∴ V – V₀   =  γ V₀ t    …………… (3)

Where ‘γ’ is a constant called a coefficient of cubical expansion

This is an expression for the coefficient of cubical expansion of a solid.

The coefficient cubical expansion is defined as an increase in volume per unit original volume at 0⁰c per unit rise in temperature.

From equation (3) we get

∴   V = V₀  +  γ V₀ t

∴   V   = V₀ (1 +    γ t) ………….. (4)

This is an expression for the volume of the body at t °C

Note: The magnitude of the coefficient of cubical expansion is so small that it is not necessary to take the initial temperature as 0 °C.

Consider a solid body of volume ‘V₁’ at temperature t₁0 °C. Let the body be heated to some higher temperature say t °C. Let ‘V₂’ be the volume of the body at temperature t₂ °C. Let ‘V0’ be the volume of the body at the temperature of 0 °C. Let γ be the coefficient of cubical-expansion, then we have

V₁  = V₀ (1 +   γ t₁) ………….. (2)

V₂  = V₀ (1 +  γ t₂) ………….. (2)

Dividing equation (2) by (1) we get

Back to List of Sub-Topics

Relation Between α and β:

Consider a thin metal plate of length, breadth, and area l₀, b₀, and A₀ at temperature 0 °C. Let the plate be heated to some higher temperature say t °C. Let l, b and A be the length, breadth, and area of the plate at temperature t °C.

Then original area   =   A₀ =   l₀ b₀ ……………..  (1)

Consider linear expansion

Length,   l =   l₀ (1+ αt)

Breadth, b = b₀ (1 + αt)

where α = coefficient of linear expansion

Final area   =    A    = l  b  =  l₀ (1+ αt) × b₀ (1 + αt)

∴   A    = l₀ b₀  (1+ 2 αt + α²t²)

Now α is very small hence α² is still small, hence quantity α²t² can be neglected

∴   A    = A₀ (1+ 2 αt)  …………  (2)

Consider superficial expansion of the plate area.

A = A₀( 1+ βt) …………  (3)

From (2) and (3)

β = 2α

Thus the coefficient of superficial expansion is twice the coefficient of linear expansion.

Back to List of Sub-Topics

Relation Between α and γ:

Consider a thin rectangular parallelopiped solid of length, breadth, height, and volume l₀, b₀, h₀, and V₀ at temperature 0 °C. Let the solid be heated to some higher temperature say t °C. Let l, b, h and V be the length, breadth, height, and volume of the solid at temperature t °C.

Then original volume    =   V₀ =   l₀ b₀ h₀   ………… (1)

Consider linear expansion

Length,   l =   l₀ (1+ αt)

Breadth, b = b₀ (1 + αt)

Height   h  = h₀ (1 + αt)

where α = coefficient of linear expansion

Final volume    =    V    =  l  b h  =  l₀ (1+ αt) × b₀ (1 + αt)× h₀ (1 + αt)

∴   V    =  l₀ b₀  h₀ (1+ 3 αt + 3 α²t² + α³t³ )

Now α is very small hence α² is still small, hence quantity α²t², α³t³ can be neglected

∴   V    =  V₀ (1+ 3 αt)  ,,,,,,,,,,,,,,,,,,  (2)

Consider cubical expansion of the solid.

V = V₀( 1+ γt) ,,,,,,,,,,,,,,,,,  (3)

From (2) and (3)

γ = 3α

Thus the coefficient of cubical expansion is the thrice coefficient of linear expansion.

Back to List of Sub-Topics

Notes: 

We have β = 2α   hence α = β/2   ………………… (1)

We have γ = 3α   hence α = γ/3   ………………… (2)

From relations (1) and (2) we get

α = β/2 = γ/3

Hence 6 α = 3 β   = 2γ

Back to List of Sub-Topics

Molecular Explanation of Expansion of Solids:

The expansion of solids at the molecular level can be understood through the principles of thermal expansion and the behaviour of atoms and molecules within the solid lattice structure.

• Vibrational Motion: Atoms and molecules within a solid are constantly in motion due to thermal energy. As the temperature of the solid increases, the average kinetic energy of the atoms and molecules also increases. This increased thermal energy causes the atoms and molecules to vibrate more vigorously about their equilibrium positions within the solid lattice.
• Increased Average Distance: The increased vibrational motion of atoms and molecules leads to an increase in the average distance between them. This phenomenon occurs because the atoms and molecules push against each other as they vibrate, causing the overall dimensions of the solid to expand.
• Interatomic Forces: The expansion of solids is influenced by the strength and nature of the interatomic or intermolecular forces within the material. In solids held together by stronger bonds, such as metallic bonds or covalent bonds, the expansion may be less pronounced compared to materials with weaker bonds, such as those held together by van der Waals forces.
• Anisotropic Expansion: Some solids exhibit anisotropic expansion, meaning they expand unequally along different crystallographic directions. This behaviour arises from the anisotropic arrangement of atoms or molecules within the crystal lattice structure. For example, in materials with layered or fibrous structures, expansion may be greater along certain directions than others.
• Phase Transitions: Phase transitions, such as melting or solid-state transformations, can also affect the expansion behaviour of solids. During phase transitions, the arrangement of atoms or molecules within the solid lattice undergoes significant changes, leading to alterations in the material’s expansion properties.
• Coefficient of Thermal Expansion: The coefficient of thermal expansion (CTE) quantifies the extent to which a material expands or contracts in response to changes in temperature. The CTE is a material-specific property that depends on factors such as the material’s composition, crystal structure, and bonding characteristics.

Thus, the expansion of solids at the molecular level is a result of the increased vibrational motion of atoms and molecules within the solid lattice structure as the temperature rises. Understanding the molecular mechanisms underlying thermal expansion is essential for various applications in materials science, engineering, and thermal management.

Back to List of Sub-Topics

For More Topics in Thermal Properties of Matter and Thermodynamics Click Here

For More Topics in Physics Click Here