Science > Physics > Stationary Waves > Vibrations of Air Columns
In this article, we shall study the vibrations of air columns in a pipe closed at one end, opened at other and in a pipe open at both ends.
Vibrations of Air Columns in a Pipe Closed at One End:
Consider a pipe closed at one end and open at the other. If a vibrating tuning fork of proper frequency is held near its open end, it sends longitudinal waves in the pipe. They are reflected from the closed end. The incident and reflected waves interfere and stationary waves are formed.
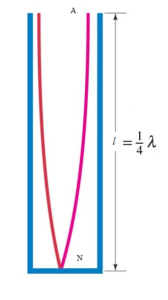
The closed-end acts as a rigid wall. The air at the closed end is not free to vibrate. Hence a node is formed at the closed end. Air at the open end is free to vibrate with maximum amplitude and antinode is formed at the open end. This is the simplest mode of vibration of an air column closed at one end and is called the fundamental mode.
If v is the velocity of sound in air at room temperature, then
v = n λ
In the fundamental mode L = λ/4, hence λ = 4 l
∴ V = nλ = 4 n l
∴ n = v /4 l
This is the frequency of the fundamental mode. Where ‘l’ is length of vibrating air column
Now consider the following figure. The same air column can also be made to vibrate so that there is a node at the closed end, an antinode at the open end, with one more node and antinode in between. In this case, the air column is said to be emitted the first overtone. If n1 is the frequency and λ1 the wavelength for the first overtone,
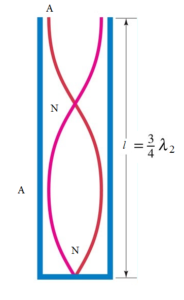

Thus the first overtone is the third harmonic.
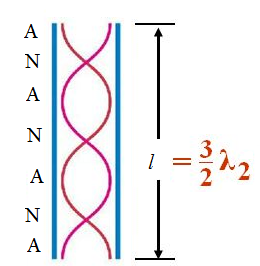
Now consider the following figure. In this case, the air column is shown emitting the second overtone. If n2 is the frequency and λ2 the wavelength for the second overtone, then


Therefore, the second overtone is the fifth harmonic.
Thus, for an air column closed at one end, only the odd harmonics are present as overtones.
For air column in a pipe closed at one end pth overtone is (2p + 1) th harmonic and the frequency of pth overtone = (2p+1)n.
Vibrations of Air Column in a Pipe Open at Both Ends:
Consider a tube open at both ends. A vibrating tuning fork held near anyone end produces longitudinal waves in the air column. They are reflected from the other end. The incident and reflected waves interface with each other and stationary waves are formed.
When an air column open at both ends is set up into vibrating, both the ends become antinodes. In the fundamental mode, as shown in the following figure, there is only one node midway between the two antinodes. Therefore, the length of the air column,


This is the fundamental frequency.
Now consider the following figure. When the air column is emitting the first overtone, there are two nodes and one antinode in between the two antinodes at the ends. Therefore, if n1 is the frequency and λ1 is the wavelength for the first overtone,


Hence, in this case, the first overtone is the second harmonic.
In the following figure, the air column is shown emitting the second overtone. If n2 is the frequency and λ2 the wavelength for the second overtone, then


The second overtone is the third harmonic.
Thus for an air column open at both ends, both odd, as well as even harmonics, are present as overtones i.e. all harmonics are present.
For air column in a pipe open at both ends pth overtone is (p + 1)th harmonic and the frequency of pth overtone = (p+1)n.
Note:
The frequency of the fundamental note of an open pipe is double that for a closed pipe of the same length.
End Correction:
It was shown by Regnault, that the antinode is not formed exactly at the open end but at a distance 0.3 d above the open end where d is the internal diameter of the tube. This additional distance called the end correction,
End correction is necessary, as the wave spreads out slightly, just above the open end, and the air particles just outside the open end are also set into vibrations. For a pipe open at one end and closed at the other
Corrected length = l + 0.3d
Hence, the velocity of sound in air at room temperature is
∴ v = nλ = 4n (l + 0.3d)
Hence, knowing n, l and d, the velocity of sound in air is determined.
For a pipe open at both ends, end correction = 2 × 0.3 d = 0.6 d
Corrected length = l + 0.6 d
Hence, the velocity of sound in air at room temperature is
∴ v = nλ = 2n ( l + 0.6d)
Elimination of End Correction:
By the usual method, we find the first resonating length (l1). Similarly, we find the second resonating length (l2) for which a loud sound is heard once again. If “e” is the end correction, then
l1 + e = λ/4 …………. (1)
l2 + e = 3λ/4 …………. (1)
Subtracting equation (1) from (2)
l2 – l1 = 3λ/4 – λ/4
∴ l2 – l1 = λ/2
∴ λ = 2( l2 – l1 )
Now, v = n λ = 2n( l2 – l1 )
Using this formula velocity of sound can be found without considering end correction.
End Correction for a Pipe Closed at One End:
If v is the velocity of sound in air, λ is the wavelength of sound. ‘l’ is the vibrating length of a pipe closed at one end, n is the frequency of vibration in the fundamental mode which is equal to the frequency of the tuning fork at time of resonance. Let ‘e’ be the end correction. This end correction depends on the diameter of the tube. we have
V = nλ= 4n ( l + e)
For the first case
V = 4n1 ( l1+ e) ………… (1)
Where l1 is a length of vibrating air column vibrating in unison with a tuning fork of frequency n1.
For the second case
V = 4n2 ( l2+ e) ………… (2)
Where l2 is a length of vibrating air column vibrating in unison with a tuning fork of frequency n2.
From (1) and (2)
4n1 ( l1+ e) = 4n2 ( l2+ e)
∴ l1n1 + en1 = l2n2 + en2
∴ l1n1 – l2n2 = en2 – en1
∴ l1n1 – l2n2 = e(n2 – n1)

End Correction for a Pipe Open at Both Ends:
If v is the velocity of sound in air, λ is the wavelength of sound. ‘l’ is the vibrating length of a pipe open at both the ends, n is the frequency of vibration in the fundamental mode which is equal to the frequency of the tuning fork at time of resonance. Let ‘e’ be the end correction. This end correction depends on the diameter of the tube. we have
V = nλ= 2n ( l + 2e)
For the first case
V = 2n1 ( l1+ 2e) ………… (1)
Where l1 is a length of vibrating air column vibrating in unison with a tuning fork of frequency n1.
For the second case
V = 2n2 ( l2+ 2e) ………… (2)
Where l2 is a of vibrating air column vibrating in unison with a tuning fork of frequency n2.
From (1) and (2)
2n1 ( l1+ 2e) = 2n2 ( l2+ 2e)
∴ l1n1 + 2en1 = l2n2 + 2en2
∴ l1n1 – l2n2 = 2en2 – 2en1
∴ l1n1 – l2n2 = 2e(n2 – n1)

Previous Topic: Melde’s Experiment
Next Topic: Concept of Resonance