Science > Physics > Wave Theory of Light > Numerical Problems on wave Theory of Light
In this article, we shall study to solve the problems on the calculation of the refractive index, angle of refraction, the wavelength of light and wavenumber of waves using snell’s law and the definition of the refractive index of the medium.
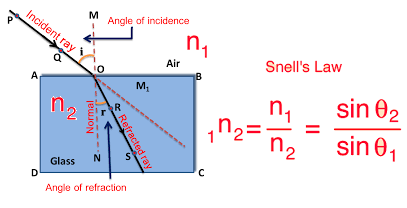
Example – 16:
The wavelength of blue light in air is 4500 Å. What is its frequency? If the refractive index of glass for blue light is 1.55, what will be the wavelength of blue light in glass?
Given: Wavelength in air = λa = 4500 Å. = 4.5 x 10-7 m, Refractive index of glass = μ = 1.55, ca = 3 x 108 m/s.
To Find: Frequency = ν =?, Wavelength in glass = λg =?
Solution:
ca = νa λa
∴ νa = ca/λa = 3 x 108/4.5 x 10-7 = 6.667 x 1015 Hz
μg = λa / λg
∴ λg = λa /μg = 4500/1.55 = 2903 Å
Ans: The frequency and wavelength of blue light are 6.667 x 1015 Hz and 2903 Å respectively.
Example 17:
A ray of light travels from air to liquid by making an angle of incidence 24° and angle of refraction of 18°. Find R.I. of liquid. Determine the wavelength of light in air and in liquid if the frequency of light is 5.4 x 1014 Hz, c = 3 x 108 m/s.
Given: Frequency of light in air = νa = 5.4 x 1014 Hz, Angle of incidence = i = 24°, Angle of refraction = r = 18°, Velocity of light in air = ca = 3 x 108 m/s.
To Find: Refractive index = μ =? Wavelength of red light in air and medium, λm = ?, λa = ?
Solution:
Refractive index of medium
μ = sin i / sin r = sin 24° / sin18° = 0.4067 / 0.3090= 1.316
In air ca = νa λa
∴ λa = ca / νa = 3 x 108 / 5.4 x 1014 = 5.555 x 10-7 m
∴ λa = 5555 x 10-10 m = 5555 Å
Now, μm = λa / λm
λm = λa / μm = 5555/1.316 = 4221 Å
Ans: Refractive index of medium = 1.316, wavelength in air is 5555 Å, wavelength in medium is 4221 Å
Example 18:
Monochromatic light of wavelength 6000 Å enters glass of R.I. 1.6. Calculate its velocity, frequency and wavelength in glass. c = 3 x 108 m/s.
Given: Wavelength of light in air = λa = 6000 Å = 6000 x 10-10 m = 6 x 10-7 m, Refractive index of medium = μ = 1.6, Velocity of light in air = ca = 3 x 108 m/s.
To Find: velocity in medium = cm=? Frquency in medium = νm = ?, Wavelength in medium, λm = ?,
Solution:
We have, μ = ca / cm
cm = ca / μm = 3 x 108 /1.6 = 1.875 x 108 m/s
In air ca = νa λa
∴ νa = ca / λa = 3 x 108 / 6 x 10-7 = 5 x 1014 Hz
If medium changes, frequency remains the same, νm = νa = 5 x 1014 Hz
Now, μ = λa / λm
λm = λa / μm = 6000/1.6 = 3750 Å
Ans: Velocity of light in medium = 1.875 x 108 m/s, frequency in medium is 5 x 1014 Hz, wavelength in medium is 3750 Å
Example 19:
Light of wavelength 5000 A.U. is incident on water surface of R.I. 4/3. . Find the frequency and wavelength of light in water if its frequency in air is 6 x 1014 Hz.
Given: Wavelength of light in air = λa = 5000 Å = 5000 x 10-10 m = 5 x 10-7 m, Refractive index of water = μ = 4/3, Velocity of light in air = ca = 3 x 108 m/s. Frequency in air = νa = 6 x 1014 Hz
To Find: Frquency in water = νw =? Wavelength in water, λw = ?,
Solution:
If medium changes, frequency remains the same, νw = νa = 6 x 1014 Hz
Now, μ = λa / λm
λm = λa / μm = 5000/(4/3) = 3750 Å
Ans: Frequency in medium is 6 x 1014 Hz, wavelength in water is 3750 Å
Example 20:
The R.I. of glass w.r.t. water is 9/8. If velocity and wavelength of light in glass are 2 x 108 m/s and 4000 Å respectively, find its velocity and wavelength in water.
Given: Wavelength of light in glass = λg = 4000 Å = 4000 x 10-10 m = 4 x 10-7 m, Refractive index of glass w.r.t. water = wμg = 9/8, Velocity of light in glass = cg = 2 x 108 m/s.
To Find: velocity in water = cw =? Wavelength in water, λw = ?,
Solution:
we have, wμg = vw / vg
vw = vg x wμg = 2 x 108 x (9/8) = 2.25 x 108 m/s
Now, wμg = λw / λg
λw = λa x wμg = 4000x(9/8) = 4500 Å
Ans: Velocity of light in water is 2.25 x 108 m/s, wavelength in water is 4500 Å
Example 21:
Find the change in wavelength of a ray of light during its passage from air to glass if the refractive index of glass is 1.5 and the frequency of the ray is 4 x 1014 Hz. Also find wave number in glass. c = 3 x 108 m/s.
Given: Frequency of light in air = νg = 4 x 1014 Hz, Refractive index of glass = μ = 1.5, Velocity of light in air = ca = 3 x 108 m/s.
To Find: Change in wavelength of light = | λa – λg | =?
Solution:
We have ca = νa λa
For air, λa = c/ν
λa = ca/νa= 3x 108 / 4 x 1014 = 7.5 x 10-7 m
λa = 7500 x 10-10 m = 7500 Å
Now, μ = λa / λg
λg = λa / μ= 7500/ 1.5= 5000 Å
Change in wavelength = λa – λg = 7500 – 5000 = 2500 Å
Wave number in glass = 1/λg = 1 /5 x 10-7 = 2 x 106 m-1.
Ans: Change in the wavelength of light is 2500 Å, Wavenumber in glass = 2 x 106 m-1.
Example 22:
The difference in velocities of a light ray in glass and in water is 2.5 x 107 m/s. R.I. of water and glass are 4/3 and 1.5 respectively. Find c.
Given: Difference in velocities = | cg – cw | = 2.5 x 107 m/s, R.I. of water = μw = 4/3, R.I. of glass = μg = 1.5
To Find: Velocity of light in air = ca =?
Solution:
μg (1.5) > μw (4/3)
Hence, cw > cg
cw – cg = 2.5 x 107
We have, for water μw = ca/cw and for glass μg = ca/cg
Hence for water cw = ca/μw and for glass cg = ca/μg
cw – cg = 2.5 x 107
∴ ca/μw – ca/μg = 2.5 x 107
∴ ca(1/μw – 1/μg) = 2.5 x 107
∴ ca(3/4 – 2/3) = 2.5 x 107
∴ ca(1/12) = 2.5 x 107
∴ ca = 12 x 2.5 x 107 = 3 x 108 m/s
Ans: Speed of light = c = 3 x 108 m/s
Example – 23:
The refractive indices of water for red and violet colours are 1.325 and 1.334 respectively. Find the difference between velocities of these two colours in water.
Given: Refractive index of red colour = μr = 1.325, Refractive index of violet colour = μv = 1.3334, Velocity of light in air = ca = 3 x 108
To Find: Difference in velocities = | cr – cv | =?
Solution:
μv (1.334) > μr (1.325)
Hence, cr > cv
We have for red light μr = ca/cr and for violet light μv = ca/cv
Hence for red light cr = ca /μr and for violet light cv = ca/μv
cr – cv = ca /μr – ca/μv
cr – cv = ca (1/μr – 1/μv)
cr – cv =3 x 108(1/1.325 – 1/1.334)
cr – cv =3 x 108(0.7547 – 0.7496)
cr – cv = 3 x 108(0.0051) = 1.53 x 108 m/s
Ans: Difference in velocities of red and violet colour in water is 1.53 x 108 m/s
Example – 24:
A parallel beam of monochromatic light is incident on glass slab at an angle of incidence of 60°. Find the ratio of the width of the beam in the glass to that in the air if the refractive index of glass is 1.5.
Given: Angle of incidence = i = 60°, Refractive index of glass = μ = 1.5.
To Find: The ratio of the width of the beam in the glass to that in the air =?
Solution:
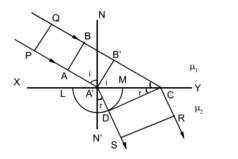
We have to find ratio CD/AB’
μ = sin i / sinr
∴ sin r = sin i / μ = sin 60o / 1.5 = 0.8660/1.5 = 0.5773
∴ r = sin-1 (0.5773) = 35o16’
In Δ AB’C, cos i = AB’ / AC ………….. (1)
In Δ ADC, cos r = CD / AC ………….. (2)
Dividing equation (2) by (1)
cos r / cos i = CD/AB’
CD/AB’ = cos 35o16’ / cos 60o
CD/AB’ = 0.8165 / 0.5 = 1.633
Ans: The ratio of the width of the beam in the glass to that in the air is 1.633
Example – 25:
A parallel beam of monochromatic light is incident on a glass slab at an angle of 45°. Find the ratio of width of beam in glass to that in air if R.I. for glass is 1.5.
Solution:
Given: Angle of incidence = i = 45°, Refractive index of glass = μ = 1.5.
To Find: The ratio of the width of the beam in the glass to that in the air =?

We have to find ratio CD/AB’
μ = sin i / sinr
∴ sin r = sin i / μ = sin 45o / 1.5 = 0.7070/1.5 = 0.4713
∴ r = sin-1 (0.4713) = 28o7’
In Δ AB’C, cos i = AB’ / AC ………….. (1)
In Δ ADC, cos r = CD / AC ………….. (2)
Dividing equation (2) by (1)
cos r / cos i = CD/AB’
CD/AB’ = cos 28o7’ / cos 45o
CD/AB’ = 0.8820 / 0.7070 = 1.25
Ans: The ratio of the width of the beam in the glass to that in the air is 1.25
Example – 26:
The wavelength of a certain light in air and in a medium is 4560 Å and 3648 Å respectively. Compare the speed of light in air with its speed in the medium.
Given: λ1 = 4560 Å, λ2 = 3648 Å.
To Find: ca/cm =?
Solution:
We have for air ca = νaλa ………….. (1)
for medium cm = νmλm ………….. (2)
Dividing equation (1) by (2)
ca / cm = λa / λm = 4560/3648 = 1.25
If medium changes, the frequency remains the same. Hence νa = νm
Hence for red light cr = ca /μr and for violet light cv = ca/μv
Ans: The ratio of the speed of light in the air with its speed in the medium is 1.25
Example – 27:
Light of wavelength 6400 Å is incident normally on a plane parallel glass slab of thickness 5 cm and μ = 1.6. The beam takes the same time to travel from the source to the incident surface as it takes to travel through the slab. Find the distance of the source from the incident surface. What is the frequency and wavelength of light in glass? c = 3 x 108 m/s.
Given: Wavelength of light = λa = 6400 Å = 6400 x 10-10 m, μ = 1.6, c = 3 x 108 m/s.
To Find: Distance of source from surface =?
Solution:
μg = ca / cg
∴ cg = ca / μg = 3 x 108 / 1.6 = 1.875 x 108 m/s
Let t be the time taken by light to travel through glass slab.
Distance travelled in glass = Speed in glass x time
time = distance /speed = (5 x 10-2)/(1.875 x 108) = 2.667 x 10-10 s
Distance of source from slab = speed x time = 3 x 108 x 2.667 x 10-10
Distance of source from slab = speed x time = 8 x 10-2 m = 8 cm
We have for air ca = νaλa
νa = ca / λa = 3 x 108 / 6400 x 10-10 =4.69 x 1014
μg = λa / λg
λg = λa / μg = 6400/1.6 = 4000 Å
Ans: Distance of source from slab = 8 cm; frequency in glass = 4.69 1014 Hz, wavelength in glass =4000 Å
Previous Topic: More Numerical Problems on wave Theory of Light
Next Topic: Polarization of Light