Kelly’s Method and Walsh Method

Management > Managerial Statistics > Index Number By Kelly’s Method and Walsh’s Method

Kelly’s Method:

Truman L. Kelly has suggested the following formula for constructing index number. Here weights are the quantities which may refer to some period, not necessarily the base year or current year. Thus the average quantity of two or more years may be used as weights. This method is known as a fixed-weighted aggregative index and is currently in great favour n the construction of index number series.

Steps Involved:

1. Denote prices of the commodity in the current year as P1 and its quantity consumed in that year by Q1.
2. Denote prices of the commodity in the base year as P₀ and its quantity consumed in that year by Q₀.
3. Find q = (Q₀ + Q₁)/2 for each commodity
4. Find the quantities P₀q and P₁q for each commodity.
5. Find sum of each column of P₀q and P₁q and denote the sums by ∑ P₀q and ∑ P₁q respectively.
6. Use following formula to find the Price index number

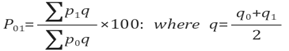
Example – 01:

Compute Price index by Kelly’s Method from the following data.

Commodity	Base Year		Current Year
	Price	Quantity	Price	Quantity
A	3	25	5	28
B	1	50	3	60
C	2	30	1	30
D	5	15	6	12

Solution:

Commodity	Base Year		Current Year
	P0	Q0	P1	Q1	q=(Q0+Q1)/2	P0q	P1q
A	3	25	5	28	16.5	49.5	82.5
B	1	50	3	60	31.5	31.5	94.5
C	2	30	1	30	31	31	15.5
D	5	15	6	12	45	45	54
Total						∑P0q=157	∑P1q=246.5

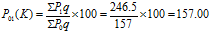
By Kelly’s method the price index number is 157.00

Walsh’s Method:

Here weights are the geometric mean of quantities of two or more years may be used as weights.

Steps Involved:

1. Denote prices of commodity in the current year as P₁ and its quantity consumed in that year by Q₁.
2. Denote prices of commodity in the base year as P₀ and its quantity consumed in that year by Q₀.
3. Find q = (Q₀ x Q₁)^1/2 = Square root of (Q₀ x Q₁) for each commodity
4. Find the quantities P₀q and P₁q for each commodity.
5. Find sum of each column of P₀q and P₁q and denote the sums by ∑ P₀q and ∑ P₁q respectively.
6. Use following formula to find the Price index number

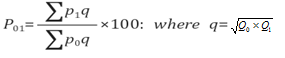
Example – 02:

Compute Price index by Walsh’s Method from the following data.

Commodity	Base Year		Current Year
	Price	Quantity	Price	Quantity
A	3	25	5	28
B	1	50	3	60
C	2	30	1	30
D	5	15	6	12

Solution:

Commodity	Base Year		Current Year
	P0	Q0	P1	Q1	q=(Q0 x Q1)1/2	P0q	P1q
A	3	25	5	28	26.46	79.37	132.29
B	1	50	3	60	54.77	54.77	164.32
C	2	30	1	30	30.00	60.00	30.00
D	5	15	6	12	13.42	67.08	80.50
Total						∑P0q=261.23	∑P1q=407.10

Thus Walsh’s price index number is 155.84

An important advantage of these formulae is that like Laspeyres index it does not demand yearly changes in the weights. Moreover, the base period can be changed without necessitating a corresponding change in the weights. This is very important because the construction of appropriate quantity weights for a general propose index usually requires a considerable amount of work.

Previous Topic: Marshall Edgeworth Method

Next Topic: Test of Adequacy of Index Number

Management > Managerial Statistics > Index Number By Kelly’s Method and Walsh’s Method