In the last article, we have studied the concept of the function and the terminology associated with it. In this article, we shall study different types of functions.
Real Function:
A function whose domain and co-domain are the set or subset of real numbers R, then the function is called a real function.
Thus if ƒ: R → R then ƒ is a real function.
Example:
Consider function y = ƒ(x) = x2 + 3x + 2
For every x ∈ R, y = ƒ(x) = x2 + 3x + 2 ∈ R,
Thus the function y = ƒ(x) = x2 + 3x + 2 is a real function.
Constant Function:
If a real function ƒ is defined as ƒ(x) = k, k is constant for all x ∈ R Then is called a constant function.
Examples:
ƒ(x) = 3, ƒ(x) = – 4 etc.
Note:
- The domain for the constant function is a set of real number R, i.e. Dƒ = R, while its range is {k}
- The range contains only one element. i.e. Rƒ = {k}
- Constant function is many-one function
- The graph for a constant function is as follows.
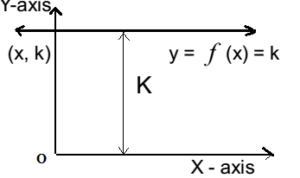
Zero Function:
For constant function k = 0 then the function is called zero function.
Example:
ƒ(x) = 0, g(x) = 0 etc
Note:
- The domain for zero function is a set of real number R i.e. Dƒ = R, while its range is {0}.
- The range contains only one element i.e. zero. i.e. Rƒ = {0}
- Zero function is many-one function.
- The graph for the zero function is as follows.
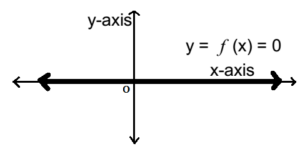
The graph is x-axis
Identity Function:
If real function ƒ is defined as ƒ(x) = x, for all x ∈ R Then ƒ is called identity function.
Example:
y = x
Note:
The domain and range for identity function is a set of real number R i.e. Dƒ = R.
The graph for the zero function is as follows.
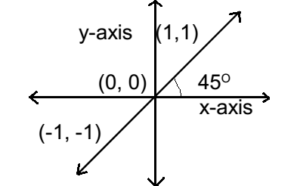
Absolute value function:
A function ƒ is defined by ƒ(x) = |x|, Where

is called an absolute value function.
Note:
The domain for absolute value function is a set of real number R i.e. Dƒ = R.
The graph for the absolute value function is as follows.

Signum function:
A function is defined by

is called signum function.
Note:
- The domain for signum function is a set of real number R i.e. Dƒ = R.
- The range of signum function contains three elements only. = {-1, 0, 1}
- The graph for the signum function is as follows.

Greatest integer function:
The greatest integer function ƒ is defined as [x], the greatest integer ≤ x, for each x ∈ R. Thus, [x] = x if x is integer and [x] = an integer immediately on the left side of x if x is not an integer.
Examples:
[5] = 5, [-6.9] = -7, [0] = 0, [2.3] = 2, [17/3] = 5
Note:
- The domain for greatest integer function is a set of real number R i.e. Dƒ = R.
- The range of greatest integer function is a set of integers. Rƒ = I
- The graph for the greatest integer function is as follows.

Fractional part function:
A functionƒ defined by ƒ(x) = x – [x], is called fractional part function.
Examples:
(3.9) =3.9 -3 = 0.9 and (-6.9) = -6.9 – (-7) = 0.1
Note:
- The domain for fractional part function is a set of real number R i.e. Dƒ = R.
- Range of fractional part function is Rƒ = [0, 1) i.e. 0 ≤ f(x) < 0
- The graph for the fractional part function is as follows.

Linear function:
A function defined by ƒ(x) = mx + c, where m, c ∈ R and m ≠ 0 is called a linear function.
Example:
ƒ(x) = y = 3x + 5
Note:
- The domain for a linear function is a set of real number R i.e. Dƒ = R.
- The range of a linear function is a set of real numbers. Rƒ = R
- The graph of a linear function is a straight line.
- If c = 0 then the graph passes through the origin.
Polynomial Function:
If real function ƒ is defined as ƒ(x) = a0 + a1x + a2x2 + a3x3 + ……… +anxn. Where a0, a1, a2, a3, …,an ∈ R and n is a whole number. Then ƒ is called as a polynomial function.
Example :
ƒ(x) = x2 + 3x + 2
Note:
- The domain and range for a polynomial function is a set of real number R. Thus, Dƒ = R. and Rƒ = = R
Reciprocal function:
A function ƒ defined by ƒ(x) = 1/x, Where x ∈ R and x ≠ 0. is called reciprocal function.
Note:
- The domain for reciprocal function is a set of real number R except x ≠ 0 i.e. Dƒ = R – {0}.
- The graph for the reciprocal function is as follows.

Exponential function:
A function ƒ defined by ƒ(x) = ex is called exponential function.
Note:
- The domain for the exponential function is a set of real number R i.e. Dƒ = R
- The graph for the exponential function is as follows.

Logarithmic function:
A function ƒ defined by ƒ(x) =log x, x > 0 is called logarithmic function.
Note:
- The domain for the logarithmic function is a set = {x| x ∈ R and x > 0}
- The graph for the logarithmic function is as follows.

Trigonometric functions:

Graphs of Trigonometric Functions:

Inverse trigonometric functions:

Some Important Results of Inverse Functions:
SET – I
- sin(sin-1x) = x, for |x|<1
- sin-1(sin x) = x, for |x| ≤ π/2
- cos(cos-1x) = x, for |x|<1
- cos-1(cos x) = x, for x = [0, π]
- tan(tan-1x) = x, ∀ x ∈ R
- tan-1(tan x) = x, for x ∈ (- π/2, π/2)
- cot(cot-1x) = x, x ∈ R
- cot-1(cot x) = x, for x ∈ (0, π)
- sec(sec-1x) = x, |x| ≥ 1
- sec-1(sec x) = x, for x ∈ [0, – π/2) ∪ (π/2, π]
- cosec(cosec-1x) = x, |x| ≥ 1
- cosec-1(cosec x) = x, for x ∈ [- π/2, 0) ∪ (0, π/2]
SET- II
- cosec-1x = sin-1(1/x)
- sec-1x = cos-1(1/x)
- cot-1x = tan-1(1/x)
SET – III
1. sin-1x + cos-1x = π/2
2. tan-1x + cot-1x = π/2
3. sec-1x + cosec-1x = π/2
SET – IV

SET – V

Rational functions:
A function ƒ of the form p(x)/q(x) = 0, q(x) ≠ 0 is called rational function. Its domain is R except for q(x) ≠ 0