Concept of a Function

Function or Mapping:

Let A and B two non-empty set and If each and every element x of set A is related by the relation ‘ƒ’ to one and only one element y of the set B such that y = ƒ(x) then such a relation ƒ from set A to set B is called a function.

In short, this is written as ƒ: A → B

Example:

Consider function y = ƒ(x) = x² + 3x + 2

Here we should know that y is an element of set B and x is an element of set A. They are related to each other by the given function ƒ(x)

Characteristics of Function:

• For each element x ∈ A, there exists a unique element y ∈ B.
• The element y ∈ B is called the image of x under the function ‘ƒ’.
• If there is an element in A which has more than one image in B then ƒ: A → B is not a function.
• If there is an element in A which has no image in B then ƒ: A → B is not a function.

Value of Function:

The value ƒ(x) = y is called the value of the function at x. Sometimes the value of the function is also referred as the image of x under function ƒ. x is known as preimage or inverse image of y.

Example:

Consider function,y = ƒ(x) = x² + 3x + 2, then

ƒ(2) = (2)² + 3(2) + 2

∴ ƒ(2) = 4 + 6 + 2

∴ ƒ(2) = 12

Thus the value of function at x = 2 is 12 or y = 12 when x = 2

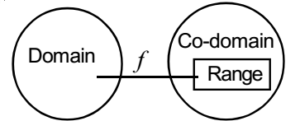
Domain and Co-domain of a Function:

The set A is called the domain of the function ‘ƒ’. The set B is called the co-domain of the function.

Example:

Consider a function y = ƒ(x) = x²

Consider set A = {1,2,3} and set B = {1,4,9,16.25}

Here we can see each and every element of set A is related to only one element in set B. hence there is a function ƒ. Then the set A is called the domain and set B is called the co-domain.

Range of Function:

The set of all values of ƒ at x i.e. {ƒ(x) = y | x ∈ A} is called the range of ƒ and it may or may not be whole of B.

Example:

Consider a function y = ƒ(x) = x²

Consider set A = {1,2,3}, then

Range = {1, 4, 9}

Range of function is a subset of co-domain of function

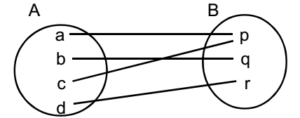
Onto Function:

If the range of ƒ = Co-domain of ƒ, then the function ƒ is called onto function.

Example:

Consider a function y = ƒ(x) = x²

Consider set A = {1,2,3} and set B = {1,4,9}

Set B is co-domain of function,

Range = {1, 4, 9}

Here Range of ƒ = Co-domain of function ƒ, hence the function is onto function.

Notes:

• On to function is also called as a surjective function or surjection.
• If ƒ: A → B then every element in B is an image of at least one element in X. Diagrammatically,

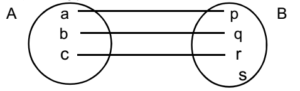
Into Function:

If the range of ƒ ≠ Co-domain of ƒ, then the function is called into function

Example:

Consider a function y = (x) = x²

Consider set A = {1,2,3} and set B = {1,4,9,16, 25}

Set B is co-domain of function,

Range = {1, 4, 9}

Here Range of ƒ ≠ Co-domain of function ƒ, hence the function is into function.

Note:

• If the function is not onto then it is into function ƒ: A →B. Diagramatically,

Method for checking whether the function ƒ: A → B is onto or into:

• Find the range of function ƒ.
• If the range of ƒ = B then the function ƒ is onto, otherwise into.

One-One Function:

When ƒ relates one element of set A to one element of set B, then the function ƒ is called one-one function,

Example:

Consider a function y = ƒ(x) = x²

Consider set A = {1,2,3} and set B = {1,4,9,16, 25}

Here function ƒ is one-one function.

Notes:

• One-one function is also called as injective function.
• For one – one function, x₁ ≠ x₂, ƒ(x₁) ≠ ƒ(x₂) for all x₁ , x₂ ∈ A
• For one – one function, x₁= x₂, ƒ(x₁) = ƒ(x₂) for all x₁ , x₂ ∈ A

One-one Correspondence:

A function ƒ from A to B is said to be one-one correspondence (bijective) iff ƒ is both one-one (injective) and onto (surjective)

Example:

Let A = {a, b, c, d} and B = {p, q, r, s}

The function ƒ: A → B defined by ƒ(a) = p, ƒ(b) = q, ƒ(c) r and ƒ(d) = s is one-one onto.

Therefore their exist a one-one correspondence. Diagrammatically

One – one onto function

One – one not onto function

The function ƒ is one-one but not onto because the element t has no preimage in A.

Neither one-one nor onto function:

The function ƒ is not one-one because the distinct elements a and c have the same image p and the function is not onto because the element r has no preimage in A.

Many – one onto function:

When ƒ relates many elements of set A to one element of set B, then the function ƒ is called many-one function,

Example:

Consider a function y = ƒ(x) = x²

Consider set A = {-1, 1, -2, 2, -3, 3}

And set B = {1,4,9,16, 25}

Here function ƒ is a many-one function.

Method for checking whether the function ƒ: A → B is one – one or many-one:

Test – 01:

• Consider any two points x, y ∈ A.
• Put ƒ(x) = ƒ(y) and solve the equation.
• If we get x = y only, then ƒ is one-one, otherwise, it is many-one.

Test – 02:

• If function ƒ is either strictly increasing or strictly decreasing in the whole domain i.e. ƒ’(x) > 0 or ƒ’(x) < 0, for all x ∈ A respectively, then it is one-one otherwise it is many-one.

Test – 03:

• If any straight line parallel to x-axis intersects the graph of the function atmost at one point, then the function is one – one, otherwise, it is many-one. In case of many – one function the line cuts the graph atleast in two distinct points.

Other Tests:

• Any continuous function having local maxima or local minima is many – one.
• All even functions are many – one.
• All polynomial of even degree defined on R have atleast one local maxima or minima and hence many – one on the domain R. Polynomial of odd degree may be one – one or may be many – one.
• If A and B are any two finite sets having m and n elements respectively, then the number of one-one function from A to B

Concept of Intervals :

Closed Interval:

Let a and b be the two real numbers such that a < b. Then, the set of all real numbers between a and b and including a and b is called a closed interval. It is denoted as [a,b], Mathematically, [a,b] = {x ∈ R, a ≤ x ≤ b }

Open Interval:

Let a and b be the two real numbers such that a < b. Then, the set of all real numbers between a and b is called open interval.
It is denoted as (a,b), Mathematically, (a,b) = {x ∈ R, a < x < b }

Semi-open Interval:

Let a and b be the two real numbers such that a < b. Then, following sets represent semi-open interval It Mathematically
[a,b)= {x R, a ≤ x < b } and (a,b]= {x R, a < x ≤ b }

Note:

• The real numbers a and b are called the endpoints of interval. ‘a’ is called the left end point and ‘b’ is called right end point.

Neighbourhoods:

Let ‘a’ be any real number and ‘δ’ be any positive real number, then the open interval (a – δ, a + δ) is called the δ-neighbourhood of a and written as” δ-nbd of a”

If x δ-nbd of a

∴ x ∈ (a – δ, a + δ)

∴ a – δ < x < a + δ

∴ – δ < x – a < a

∴  | x – a| < δ

Thus a is center and 2δ is the length of δ-neighbourhood of a

Deleted δ-neighborhood of a:

If δ-neighbourhood of ‘a’ is defined by deleting the center a, then the neighbourhood obtained is called deleted δ-neighbourhood of a.
Mathematically, The deleted δ-neighbourhood of a is given by

{x ∈ (a – δ < x < a + δ), x ≠ a} or

{x | x (a – δ, a + δ) , x ≠ a}

In the modulus form, it is written as

0 < |x – a| < δ

One-sided neighborhoods:

If a, b, c R such that a < c < b then

• (a, c] is called left neighbourhood of c.
• [c, b) is called right neighbourhood of c.
• (a, c) is called left deleted neighbourhood of c.
• (c, b) is called right deleted neighbourhood of c.