Standard unit circle and its ue to find trigonometric ratios of angles

In this article, we shall find values of trigonometric ratios of standard angles in the third and the fourth quadrants using a standard unit circle.

Trigonometric Ratios of 210^o or (7π/6)^c:

Let us consider a standard unit circle

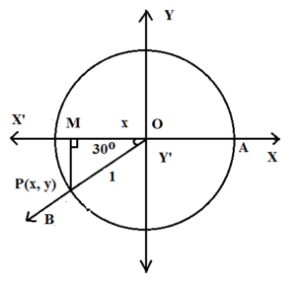
Let m∠ AOP = θ = 210^o = (7π/6)^c

m∠ POM = 30^o

Ray OA is the initial arm of the angle.

The terminal arm of the angle ray OP intersects the circle at P(x, y)

Let PM be perpendicular to OX’. Thus ΔOMP is 30^o-60^o-90^o triangle

PM = 1/2(OP) = 1/2 (1) = 1/2 (side opposite to 30^o)

OM = √3/2(OP) = √3/2 (1) = √3/2 (side opposite to 60^o)

Point P is in the third quadrant

Hence x = -√3/2 an y = -1/2. Thus

sin 210^o = y = – 1/2

cos 210^o = x = – √3/2

tan 210^o = y/x = (-1/2)/(-√3/2) = 1/√3

cosec 210^o = 1/y = 1/(-1/2) = – 2

sec 210^o = 1/x = 1/(-√3/2) = – 2/√3

cot 210^o = x/y = (-√3/2)/(-1/2) = √3

sin 210^o sin (7π/6)^c	cos 210^o cos (7π/6)^c	tan 210^o tan (7π/6)^c	cosec 210^o cosec (π/6)^c	sec 210^o sec (7π/6)^c	cot 210^o cot (7π/6)^c
– 1/2	– √3/2	1/√3	– 2	– 2/√3	√3

Trigonometric Ratios of 225^o or (5π/4)^c:

Let us consider a standard unit circle

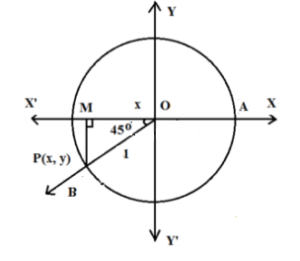
Let m∠ AOP = θ = 225^o = (5π/4)^c

m∠ POM = 45^o

Ray OA is the initial arm of the angle.

The terminal arm of the angle ray OP intersects the circle at P(x, y)

Let PM be perpendicular to OX’. Thus ΔOMP is 45^o-45^o-90^o triangle

PM = 1/√2(OP) = 1/√2 (1) = 1/√2 (side opposite to 45^o)

OM = 1/√2(OP) = 1/√2 (1) = √1/√2 (side opposite to 45^o)

Point P is in the third quadrant

Hence x = – 1/√2 an y = – 1/√2. Thus

sin 225^o = y = – 1/√2

cos 225^o = x = – 1/√2

tan 22^o = y/x = (-1/√2)/(- 1/√2) = 1

cosec 225^o = 1/y = 1/(-1/√2) = – √2

sec 225^o = 1/x = 1/(-1/√2) = – √2

cot 225^o = x/y = (-1/√2)/(-1/√2) = 1

sin 225^o sin (5π/4)^c	cos 225^o cos (5π/4)^c	tan 225^o tan (5π/4)^c	cosec 225^o cosec (5π/4)^c	sec 225^o sec (5π/4)^c	cot 225^o cot (5π/4)^c
– 1/√2	– 1/√2	1	– √2	– √2	1

Trigonometric Ratios of 240^o or (4π/3)^c:

Let us consider a standard unit circle

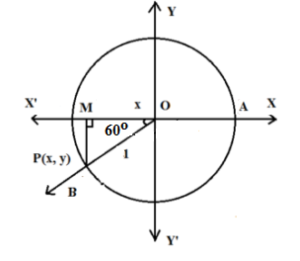
Let m∠ AOP = θ = 240^o = (4π/3)^c

m∠ POM = 60^o

Let PM be perpendicular to OX’. Thus ΔOMP is 30^o-60^o-90^o triangle

PM = √3/2(OP) = 1/2 (1) = √3/2 (side opposite to 60^o)

OM = 1/2(OP) = √3/2 (1) = 1/2 (side opposite to 30^o)

Point P is in the third quadrant

Hence x = – 1/2 an y = – √3/2. Thus

sin 240^o = y = – √3/2

cos 240^o = x = -1/2

tan 240^o = y/x = (-√3/2)/(-1/2) = √3

cosec 240^o = 1/y = 1/(-√3/2) = – 2/√3

sec 240^o = 1/x = 1/(-1/2) = – 2

cot 240^o = x/y = (-1/2)/(-√3/2) = 1/√3

sin 240^o sin (4π/3)^c	cos 240^o cos (4π/3)^c	tan 240^o tan (4π/3)^c	cosec 240^o cosec (4π/3)^c	sec 240^o sec (4π/3)^c	cot 240^o cot (4π/3)^c
– √3/2	-1/2	√3	– 2/√3	– 2	1/√3

Trigonometric Ratios of 270^o or (3π/2)^c:

Let us consider a standard unit circle

Let m∠ AOP = θ = 270^o = (3π/2)^c

Let PM be perpendicular to OX. M coicides with O

PM = 1 and OM = 0

Point P is on negative y-axis

Hence x = 0 an y = -1. Thus

sin 270^o = y = -1

cos 270^o = x = 0

tan 270^o = y/x (Not defined since x = 0)

cosec 270^o = 1/y = 1/-1 = -1

sec 270^o = 1/x (Not defined since x = 0)

cot 270^o = x/y = 0/-1 = 0

sin 270^o sin (π/2)^c	cos 270^o cos (π/2)^c	tan 270^o tan (π/2)^c	cosec 270^o cosec (π/2)^c	sec 270^o sec (π/2)^c	cot 270^o cot (π/2)^c
– 1	0	–	– 1	–	0

Trigonometric Ratios of 300^o or (5π/3)^c:

Let us consider a standard unit circle

Let m∠ AOP = θ = 300^o = (5π/3)^c

Let PM be perpendicular to OX. Thus ΔOMP is 30^o-60^o-90^o triangle

PM = √3/2(OP) = 1/2 (1) = √3/2 (side opposite to 60^o)

OM = 1/2(OP) = √3/2 (1) = 1/2 (side opposite to 30^o)

Point P is in the fourth quadrant

Hence x = 1/2 an y = – √3/2. Thus

sin 300^o = y = – √3/2

cos 300^o = x = 1/2

tan 300^o = y/x = (-√3/2)/(1/2) = – √3

cosec 300^o = 1/y = 1/(- √3/2) = – 2/√3

sec 300^o = 1/x = 1/(1/2) = 2

cot 300^o = x/y = (1/2)/(- √3/2) = – 1/√3

sin 300^o sin (5π/3)^c	cos 300^o cos (5π/3)^c	tan 300^o tan (5π/3)^c	cosec 300^o cosec (5π/3)^c	sec 300^o sec (5π/3)^c	cot 30^o cot (5π/3)^c
– √3/2	1/2	– √3	– 2/√3	2	– 1/√3

Trigonometric Ratios of 315^o or (7π/4)^c:

Let us consider a standard unit circle

Let m∠ AOP = θ = 315^o = (7π/4)^c

Ray OA is the initial arm of the angle.

The terminal arm of the angle ray OP intersects the circle at P(x, y)

Let PM be perpendicular to OX. Thus ΔOMP is 45^o-45^o-90^o triangle

PM = 1/√2(OP) = 1/√2 (1) = 1/√2 (side opposite to 45^o)

OM = 1/√2(OP) = 1/√2 (1) = 1/√2 (side opposite to 45^o)

Point P is in the fourth quadrant

Hence x = 1/√2 an y = -1/√2. Thus

sin 315^o = y = – 1/√2

cos 315^o = x = √1/√2

tan 315^o = y/x = (-1/√2)/(1/√2) = – 1

cosec 315^o = 1/y = 1/(-1/√2) = – √2

sec 315^o = 1/x = 1/(1/√2) = √2

cot 315^o = x/y = (1/√2)/(-1/√2) = – 1

sin 315^o sin (7π/4)^c	cos 315^o cos (7π/4)^c	tan 315^o tan (7π/4)^c	cosec 315^o cosec (7π/4)^c	sec 315^o sec (7π/4)^c	cot 315^o cot (7π/4)^c
– 1/√2	1/√2	– 1	– √2	√2	– 1

Trigonometric Ratios of 330^o or (11π/6)^c:

Let us consider a standard unit circle

Let m∠ AOP = θ = 330^o = (11π/6)^c

Ray OA is the initial arm of the angle.

The terminal arm of the angle ray OP intersects the circle at P(x, y)

Let PM be perpendicular to OX. Thus ΔOMP is 30^o-60^o-90^o triangle

PM = 1/2(OP) = 1/2 (1) = 1/2 (side opposite to 30^o)

OM = √3/2(OP) = √3/2 (1) = √3/2 (side opposite to 60^o)

Point P is in the fourth quadrant

Hence x = √3/2 an y = – 1/2. Thus

sin 330^o = y = – 1/2

cos 330^o = x = √3/2

tan 330^o = y/x = (-1/2)/(√3/2) = – 1/√3

cosec 330^o = 1/y = 1/(-1/2) = – 2

sec 330^o = 1/x = 1/(√3/2) = 2/√3

cot 330^o = x/y = (√3/2)/(-1/2) = – √3

sin 330^o sin (11π/6)^c	cos 330^o cos (11π/6)^c	tan 330^o tan (11π/6)^c	cosec 330^o cosec (11π/6)^c	sec 330^o sec (11π/6)^c	cot 330^o cot (11π/6)^c
– 1/2	√3/2	– 1/√3	– 2	2/√3	– √3

Trigonometric Ratios of 360^o or 2π^c:

Let us consider a standard unit circle

Let m∠ AOP = θ = 360^o = 2π^c

Ray OA is the initial arm of the angle.

The terminal arm of the angle ray OP intersects the circle at P(1, 0)

Hence x = 1 an y = 0. Thus

sin 360^o = y = 0

cos 360^o = x = 1

tan 360^o = y/x = 0/1 = 0

cosec 360^o = 1/y (Not defined since y = 0)

sec 360^o = 1/x = 1/1 = 1

cot 360^o = x/y (Not defined since y = 0)

sin 360^o sin (π)^c	cos 360^o cos (π)^c	tan 360^o tan (π)^c	cosec 360^o cosec (π)^c	sec 360^o sec (π)^c	cot 360^o cot (π)^c
0	1	0	–	1	–

Leave a Reply Cancel reply