In this article, we shall study to find signs of trigonometric ratios (Functions) in different quadrants formed due to co-ordinate axes.
Signs of Trigonometric Ratios in Different Quadrants:
| θ lies in Quadrant → | I | II | III | IV |
| Trigonometric Functions↓ | ||||
| sin θ | + ve | + ve | – ve | – ve |
| cos θ | + ve | – ve | – ve | + ve |
| tan θ | + ve | – ve | + ve | – ve |
| cosec θ | + ve | + ve | – ve | – ve |
| sec θ | + ve | – ve | – ve | + ve |
| cot θ | + ve | – ve | + ve | – ve |
Diagram Showing Signs of Trigonometric Ratios in Different Quadrants
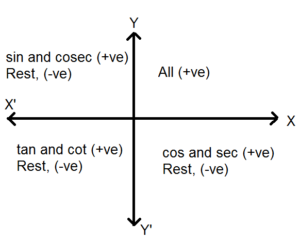
Diagram showing value of angle in different quadrants:

Examples Based on Signs of Trigonometric Ratios:
Example – 01:
State the signs of following Trigonometric Ratios (Functions)
sin 675o
sin 675 o = sin (360o + 315o) = sin (315o) = sin (270o + 45o)
Thus the angle 675o lies in the fourth quadrant, where sin function is negative.
Hence sin 675 o is negative
sin 159o
sin 159 o = sin (90o + 69o)
Thus the angle 159o lies in second quadrant, where sin function is positive.
Hence sin 159 o is positive
cos 573 o
cos 573 o = cos (360o + 213o) = cos (213o) = sin (180o + 33o)
Thus the angle 573o lies in the third quadrant, where cos function is negative.
Hence cos 573 o is negative
cos 250 o
cos 250 o = cos (180o + 70o)
Thus the angle 250o lies in the third quadrant, where cos function is negative.
Hence cos 250 o is negative
cos (-8π/3)c
cos(-8π/3)c = cos (-2π – 2π/3) = cos (- 2π/3) = cos (- π/2 – π/6)
Thus the angle (-8π/3)c lies in the third quadrant, where cos function is negative.
Hence cos(-8π/3)c is negative
cos (11π/9)c
cos(11π/9)c = cos (π + 2π/9)
Thus the angle (11π/9)c lies in the third quadrant, where cos function is negative.
Hence cos(11π/9)c is negative
sec (3π/5)c
sec(3π/5)c = sec (π/2 + π/10)
Thus the angle (3π/5)c lies in the second quadrant, where sec function is negative.
Hence sec(3π/5)c is negative
Example – 02:
Determine the quadrant in which θ lies from following trigonometric functions.
sin θ > 0 and sec θ < 0
Given, sin θ > 0 and sec θ < 0. i.e. sin θ is positive and sec θ is negative
Hence θ lies in the second quadrant.
cos θ < 0 and cot θ > 0
Given, cos θ < 0 and cot θ > 0, i.e. cos θ is negative and cot θ is positive
Hence θ lies in the third quadrant.
sec θ > 0 and cosec θ < 0
Given, sec θ > 0 and cosec θ < 0, i.e. sec θ is positive and cosec θ is negative
Hence θ lies in the fourth quadrant.
Example – 04:
If tan θ= -2 and θ lies in second quadrant, find values of other trigonometric functions.
Solution:
Given tan θ = -2
We have, 1+ tan2θ = sec2θ
∴ 1+ (-2)2 = sec2θ
∴ 5 = sec2θ
∴ sec θ = ± √5
Now θ lies in second quadrant where sec ratio is negative.
∴ sec θ = – √5
∴ cos θ = – 1/√5
Now, tan θ = sin θ / cos θ
∴ sin θ = tan θ x cos θ = (-2) x ( – 1/√5) = 2/√5
Now, cot θ = 1/ tan θ = 1/-2 = – 1/2
cosec θ = 1/sin θ = 1/(2/√5) = √5/2
Example – 05:
If tan θ = 5/12 and π < θ < 3π/2, find values of other trigonometric functions.
Solution:
Given tan θ = 5/12 and π < θ < 3π/2
We have, 1+ tan2θ = sec2θ
∴ 1+ (5/12)2 = sec2θ
∴ 1 + 25/144 = sec2θ
∴ (144 + 25)/144 = sec2θ
∴ 169/144 = sec2θ
∴ sec θ = ± 13/12
Now π < θ < 3π/2, hence θ lies in the third quadrant where sec ratio is negative.
∴ sec θ = – 13/12
∴ cos θ =1/(- 13/12) = – 12/13
Now, tan θ = sin θ / cos θ
∴ sin θ = tan θ x cos θ = (5/12) x ( – 12/13) = – 5/13
Now, cot θ = 1/ tan θ = 1/( 5/12 )= 12/5
cosec θ = 1/sin θ = 1/(- 5/13) = – 13/5
Example – 06:
If cos θ= 4/5 and 3π/2 < θ < 2π, find values of other trigonometric functions.
Solution:
Given cos θ= 4/5 and 3π/2 < θ < 2π
We have, sin2θ + cos2θ = 1
∴ sin2θ + (4/5)2 = 1
∴ sin2θ = 1 – 16/25
∴ sin2θ = (25 – 16)/25
∴ sin2θ = 9/25
∴ sin θ = ± 3/5
Now 3π/2 < θ < 2π, hence θ lies in the fourth quadrant where sin ratio is negative.
∴ sin θ = – 3/5
Now, tan θ = sin θ / cos θ
∴ tan θ = (- 3/5) / (4/5) = – 3/4
Now, cosec θ = 1/sin θ = 1/(- 3/5) = – 5/3
sec θ = 1/cos θ = 1/(4/5) = 5/4
cot θ = 1/ tan θ = 1/( -3/4 )= – 4/3
Example – 07:
If tan θ= – 4/3 and 3π/2 < θ < 2π, find values of 3 sec θ + 5 tan θ.
Solution:
Given tan θ = – 4/3 and 3π/2 < θ < 2π
We have, 1+ tan2θ = sec2θ
∴ 1+ (-4/3)2 = sec2θ
∴ 1 + 16/9 = sec2θ
∴ (9 + 16)/9 = sec2θ
∴ 25/9 = sec2θ
∴ sec θ = ± 5/3
Now 3π/2 < θ < 2π, hence θ lies in the fourth quadrant where sec ratio is positive.
∴ sec θ = 5/3
Now, 3 sec θ + 5 tan θ = 3 x (5/3) + 5 x (-4/3) = 5 – 20/3 = (15 – 20)/3 = – 5/3
Example – 08:
If sec θ= √2 and 3π/2 < θ < 2π, find values of
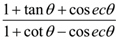
Solution:
Given sec θ= √2 and 3π/2 < θ < 2π
We have,1 + tan2θ = sec2θ
∴ 1 + tan2θ = (√2)2
∴ 1 + tan2θ = 2
∴ tan2θ = 1
∴ tan θ = ± 1
Now 3π/2 < θ < 2π, hence θ lies in the fourth quadrant where tan ratio is negative.
∴ tan θ = – 1
Now cot θ = 1/tan θ = 1 /(-1) = -1
cos θ = 1/sec θ = 1/√2
tan θ = sin θ / cos θ
∴ sin θ = tan θ x cos θ = (-1) x ( 1/√2) = – 1/√2
cosec θ = 1/sin θ = 1/(- 1/√2) = – √2

Example – 09:
If cos θ= – 3/5 and π < θ < 3π/2, find value of

Solution:
Given cos θ= – 3/5 and π < θ < 3π/2
We have, sin2θ + cos2θ = 1
∴ sin2θ + (- 3/5)2 = 1
∴ sin2θ = 1 – 9/25
∴ sin2θ = (25 – 9)/25
∴ sin2θ = 16/25
∴ sin θ = ± 4/5
Now π/ < θ < 3π/2, hence θ lies in the thir quadrant where sin ratio is negative.
∴ sin θ = – 4/5
Now, tan θ = sin θ / cos θ
∴ tan θ = (- 4/5) / (- 3/5) = 4/3
Now, cosec θ = 1/sin θ = 1/(- 4/5) = – 5/4
sec θ = 1/cos θ = 1/(- 3/5) = – 5/3
cot θ = 1/ tan θ = 1/( 4/3 )= 3/4

Example – 10:
If 5 tan A = √7 where π < A < 3π/2 and sec B = √11 where 3π/2 < B < 2π, find value of cosec A – tan B.
Solution:
Given 5 tan A = √7 where π < A < 3π/2
∴ tan A = √7/5
∴ cot A = 5/√7
We have,1 + cot2A = cosec2A
∴ 1 + (5/√7)2 = cosec2A
∴ 1 + (25/7) = cosec2A
∴ (7 + 25)/7 = cosec2A
∴ cosec2A = 32/7
∴ cosec A = ± √32/√ 7 = ± 4√2/√ 7
Now π < A < 3π/2, hence A lies in the third quadrant where cosec ratio is negative.
cosec A = – 4√2/√ 7
Given sec B = √11 where 3π/2 < B < 2π
We have,1 + tan2B = sec2B
∴ 1 + tan2B = (√11)2
∴ 1 + tan2B = 11
∴ tan2B = 10
∴ tan B = ± √10
Now 3π/2 < B < 2π, hence B lies in the fourth quadrant where tan ratio is negative.
∴ tan B = – √10
The value of the quantity cosec A – tan B = – 4√2/√7 – √10
Example – 11:
Find the value of 4 cos A + 3 cos B if angles A and B lies in second quadrants and

Solution:
sin A = 3/5 and sin B = 4/5
We have, sin2A + cos2A = 1
∴ (3/5)2 + cos2A = 1
∴ cos2A = 1 – 9/25
∴ cos2A = (25 – 9)/25
∴ cos2A = 16/25
∴ cosA = ± 4/5
Now A lies in the second quadrant where cos ratio is negative.
∴ cosA = – 4/5
sin B = 4/5
We have, sin2B + cos2B = 1
∴ (4/5)2 + cos2B = 1
∴ cos2B = 1 – 16/25
∴ cos2B = (25 – 16)/25
∴ cos2B = 9/25
∴ cosB = ± 3/5
Now A lies in the second quadrant where cos ratio is negative.
∴ cosA = – 3/5
The value of
4 cos A + 3 cos B = 4 x (- 4/5) + 3 x (- 3/5)= -16/5 – 9/5 = -25/5 = -1
Example – 12:
If 2 sin x = 1, π/2 < x < π and √2 cos y = 1, 3π/2 < y < 2π, find the value of

Solution:
2sin x = 1, hence sin x = 1/2, π/2 < x < π
We have, sin2x + cos2x = 1
∴ (1/2)2 + cos2x = 1
∴ cos2x = 1 – 1/4
∴ cos2x = (4-1)/4
∴ cos2x = 3/4
∴ cos x = ± √3/2
Now x lies in the second quadrant where cos ratio is negative.
∴ cos x = – √3/2
Now, tan x = sin x/ cos x = (1/2)/(- √3/2) = – 1/√3
√2 cos y = 1, hence cos y = 1/√2, 3π/2 < y < 2π
We have, sin2y + cos2y = 1
∴ sin2y + (1/√2)2 = 1
∴sin2y = 1 – 1/2
∴ sin2y = (2 – 1)/2
∴ sin2y = 1/2
∴ sin y = ± 1/√2
Now y lies in the third quadrant where sin ratio is negative.
∴ sin y = – 1/√2
Now, tan y = sin y/ cos y = ( – 1/√2)/(1/√2) = – 1

Example – 13:
If cos A = sin B = -1/3, where π/2 < A < π and π < B< 3π/2, then find the value of

Solution:
Given cos A = -1/3, π/2 < x < π
We have, sin2A + cos2A = 1
∴ sin2A + (-1/3)2 = 1
∴ sin2A = 1 – 1/9
∴ sin2A = (9-1)/9
∴ sin2A = 8/9
∴ sin A = ± 2√2/3
Now A lies in the second quadrant where sin ratio is positive.
∴ sin A = 2√2/3
Now, tan A = sin A/ cos A = (2√2/3) / (- 1/3)= – 2√2
sin B = – 1/3, π < B< 3π/2
We have, sin2B + cos2B = 1
∴(- 1/3)2 + cos2B = 1
∴ cos2B = 1 – 1/9
∴ cos2B = (9 – 1)/9
∴ cos2B = 8/9
∴ cos B = ± 2√2/3
Now y lies in the second quadrant where cos ratio is negative.
∴ cos B = – 2√2/3
Now, tan B = sin B/ cos B = ( – 1/3)/(- 2√2/3) = 1/2√2
