Science > Physics > Stationary Waves > Numerical Problems Vibration of String Set-01
In this article, we shall study to solve problems to calculate fundamental frequency of vibration of string and its higher frequencies.
Important Formulae:
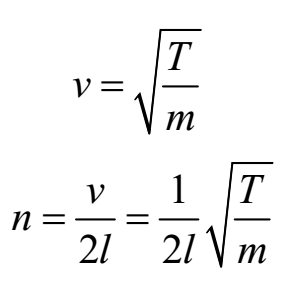
For vibrating string pth overtone is (p + 1)th harmonic
Frequency of qth harmonic = q x n
Frequency of qth overtone = (q + 1) x n
Law of length (Tension in wire T and Linear density of wire m constant):
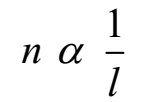
Law of tension (Length of wire l and linear density of wire m constant):
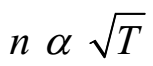
Law of mass (Length of wire l and Tension in wire T constant):

Law of diameter (Length of wire l and Tension in wire T constant):

Law of density (Length of wire l and Tension in wire T constant):

Where
n = Fundamental frequency of vibration of string
v = Velocity of wave in the string
T = Tension in the string
l = Vibrating length of string
m = M/L = Linear density of wire
M = Mass of wire
L = Length of wire
d = diameter of wire
ρ = Density of material of wire
Example 01:
When the length of wire between the bridges of a sonometer is 20 cm, it resonates with a frequency of 512 Hz. What is the velocity of transverse waves along the wire of the sonometer?
Given: Vibrating length of wire = l = 20 cm = 0.2 m, Frequency of vibration = n = 512 Hz,
To Find: Velocity of wave = v =?
Solution:
For fundamental mode of vibration wavelength of wave
λ = 2l = 2 × 0.2 = 0.4 m
We have v = nλ
∴ v = 512 × 0.4 = 204.8 m s-1
Ans: Velocity of the wave = 204.8 m s-1
Example 02:
The length of a stretched wire is 1 m and its fundamental frequency is 300 Hz. What is the speed of the transverse wave in the wire?
Given: Vibrating length of wire = l = 1 m, Frequency of vibration = n = 300 Hz,
To Find: Velocity of wave = v =?
Solution:
For fundamental mode of vibration wavelength of wave
λ = 2l = 2 × 1 = 2 m
We have v = nλ
∴ v = 300 × 2 = 600 m s-1
Ans: Velocity of the wave = 600 m s-1
Example 03:
A thin wire one metre long, weighing 0.002 kg, is stretched by a weight of 9 kg. Find the velocity of transverse waves set up on the wire when plucked. What is the frequency of the fundamental note emitted by the wire? What is the frequency of the second harmonic?
Given: Vibrating length of wire = l = 1 m, Mass of the wire = M = 0.002 kg, Tension in wire = T = 9 kg-wt = 9 × 9.8 N,
To Find: Velocity of wave = v =? Frequency of fundamental mode =?, Frequency of second harmonic = ?
Solution:
Linear density = m = M/l = 0.002/1
∴ m = 0.002 kg m-1
Velocity of wave in the wire is given by

Fundamental frequency of vibration is given by

Frequency of fundamental mode = 105 Hz
Frequency of second harmonic = 2n = 2 × 105 = 210 Hz
Ans: The velocity of wave = 210 m s-1, the frequency of fundamental mode = 105 Hz, and the frequency of second harmonic = 210 Hz
Example 04:
A thin wire 80 cm long, having linear density 4 x 10-5 kg m-1 is stretched by a weight of 8 kgf. Find the velocity of transverse waves set up on the wire when plucked. What is the frequency of the fundamental note emitted by the wire? What is the frequency of the second overtone?
Given: Vibrating length of wire = l = 80 cm = 80 x 10-2 m, Linear density of wire = 4 x 10-5 kg m-1, Tension in wire = T = 8 kgf = 8 x 9.8 N,
To Find: Velocity of wave = v =? Frequency of fundamental mode =?, Frequency of second overtone = ?
Solution:
Velocity of wave in the wire is given by

Fundamental frequency of vibration is given by

Frequency of fundamental mode = 875 Hz
For vibrating string second overtone is third harmonic
Frequency of second overtone = 3n = 3 x 875 = 2625 Hz
Ans: The velocity of wave = 1400 m/s, the frequency of fundamental mode = 875 Hz, and the frequency of second overtone = 2625 Hz
Example 05:
A sonometer wire is under tension of 40 N and the length between the bridges is 50 cm. A meter long wire of sonometer has mass of 1.0 g. Determine its fundamental frequency.
Given: Vibrating length of wire = l = 50 cm = 50 x 10-2 m, Mass of wire = M = 1.0 g = 1 x 10-3 kg , Length of Wire = L = 1 m, Tension in wire = T = 40 N,
To Find: Fundamental frequency =?
Solution:
Linear Density = M/ L = 1 x 10-3 /1 = 1 x 10-3 kg m-1

Ans: Fundamental frequency = 200 Hz
Example 06:
A wire of length 0.5 m is stretched by a weight of 2 kg. If the mass per unit length of the wire is 1.96 × 10-3 kg m-1, find the fundamental frequency of the wire and the frequency of its first overtone. (g = 9.8 m s-2)
Given: Vibrating length of wire = l = 0.5 m, Linear density of wire = 1.96 × 10-3 kg m-1, Tension in wire = 2 kg-wt = 2 × 9.8 N,
To Find: Frequency of fundamental mode =? Frequency of first overtone =?
Solution:
Fundamental frequency of vibration is given by

For vibrating string, the first overtone is second harmonic
Hence, frequency of first overtone = 2n = 2 × 100 = 200 Hz
Ans: Frequency of fundamental mode = 100 Hz and the frequency of first overtone = 200 Hz
Example 07:
A wire of length 0.5 m is stretched by a weight of 2 kg. If the mass per unit length of the wire is 1.96 × 10-3 kg m-1, find the fundamental frequency of the wire and the frequency of its first overtone. (g = 9.8 m s-2)
Given: Vibrating length of wire = l = 0.5 m, Linear density of wire = 1.96 × 10-3 kg m-1, Tension in wire = 2 kg-wt = 2 × 9.8 N,
To Find: Frequency of fundamental mode =? Frequency of first overtone =?
Solution:
Fundamental frequency of vibration is given by

For vibrating string, the first overtone is second harmonic
Hence, frequency of first overtone = 2n = 2 × 100 = 200 Hz
Ans: Frequency of fundamental mode = 100 Hz and the frequency of first overtone = 200 Hz
Example 08:
The mass of a 1 m long steel wire is 20 g. The wire is stretched under a tension of 800 N. What are the frequencies of its fundamental mode of vibration and the next three higher modes?
Given: Vibrating length of wire = l = 1 m, Mass of wire = M = 20 g = 20 x 10-3 kg , Length of Wire = L = 1 m, Tension in wire = T = 800 N,
To Find: Fundamental frequency =?
Solution:
Linear Density = M/ L = 20 x 10-3 /1 = 20 x 10-3 kg m-1

Fundamental frequency = 100 Hz
Frequency of second harmonic = 2n = 2 x 100 = 200 Hz
Frequency of third harmonic = 3n = 3 x 100 = 300 Hz
Frequency of fourth harmonic = 4n = 4 x 100 = 400 Hz
Example 09:
A metal wire of linear mass density of 9.8 g m-1 is stretched with a tension of 10 kg wt between two rigid supports 1 m apart. The wire passes at its middle point between the poles of permanent magnet and it vibrates in resonance, when carrying an alternating current of frequency n. Find the frequency of the alternating source.
Given: Vibrating length of wire = l = 0.5 m, Linear density of wire = 9.8 g m-1 = 9.8 × 10-3 kg m-1, Tension in wire = 10 kg-wt = 10 × 9.8 N,
To Find: Frequency of alternating source =?
Solution:
Fundamental frequency of vibration is given by

Now the vibrating string is in resonance with the alternating source.
Frequency of alternating source = 50 Hz
Example 10:
Calculate the fundamental frequency of a sonometer wire of length = 20 cm, tension 25 N, cross-sectional area = 10-2 cm2 and density of material of wire 104 kg m-3.
Given: Vibrating length of wire = 20 cm = 20 x 10-2 m, Tension = T = 25 N, Cross-sectional area = A = 10-2 cm2 = 10-2 x 10-4 m2 = 10-6 m2, Density of material of wire = rho = 104 kg m-3.
To Find: Fundamental frequency = n =?
Solution:
Linear density = m = A x 1 x rho
Linear density = m = 10-6 x 1 x 104 = 10-2 kg m-1
Fundamental frequency of vibration is given by

Ans: Fundamental frequency is 125 Hz
Example 11:
The length of sonometer wire is 0.75 m and density 9 x 103 kg m-3. It can bear stress of 8.1 x 108 N m-2 without exceeding the elastic limit. What is the fundamental frequency that can be produced in the wire?
Given: Vibrating length of wire = 0.75 m, Density of material of wire = rho = 9 x 103 kg m-3, Stress = 8.1 x 108 N m-2.
To Find: Fundamental frequency = n =?
Solution:
Let A be the cross-sectional area of the wire.
Stress = F/A = T/A
T = Stress x A ……. (1)
Linear density = m = A x 1 x ρ ……… (2)
Fundamental frequency of vibration is given by

Ans: Fundamental frequency = 200 Hz
Example 12:
What should be the tension applied to a wire of length 0.8 m and mass 5 g if it is to vibrate with a fundamental frequency of 100Hz?
Given: Length of wire = l = 0.8 m, Mass of wire = M = 5 g = 5 × 10-3 kg, Frequency of fundamental mode = n = 100 Hz
To Find: Tension in wire =?
Solution:
Linear density = m = M/l = 5 × 10-3/0.8 = 6.25 × 10-3 kg m-1
Fundamental frequency of vibration is given by

Ans: Tension applied = 160 N
Example 13:
A sonometer wire of length 0.5 m is stretched by a weight of 5 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of the material of wire.
Given: Length of wire = l = 0.5 m, Tension in wire = 5 kg = 5 × 9.8 N, Frequency of fundamental mode = n = 100 Hz
To Find: Linear density =?
Solution:
Fundamental frequency of vibration is given by

Ans: Linear density of material of wire = 4.9 × 10-3 kg m-1
Example 14:
A sonometer wire of length 0.7m is stretched by a weight of 4 kg. The fundamental frequency of vibration of the wire is 200 Hz. Determine the linear density of the wire.
Given: Vibrating length = l = 0.7 m, Tension = 4 kg-wt = 4 x 9.8 N, Fundamental frequency = n = 200 Hz.
To Find: Linear density of wire = m =?
Solution:
Fundamental frequency of vibration is given by

Ans: Linear density of wire 5 x 10-4 kg m-1
Example 15:
A metal wire of length 20 cm and diameter 0.2 mm is stretched by a load of 2 kg. The density of material of the wire is 8000 kg m-3. Find the fundamental frequency of vibrations of the wire. g = 9.8m s-2.
Given: Vibrating length = l = 20 cm = 20 x 10-2 m, Diameter of wire = d = 0.2 mm = 0.2 x 10-3 m = 2 x 10-4 m, Density of material of wire = ρ = 8000 kg m-3, Tension = 2 kg-wt = 2 x 9.8 N.
To Find: Fundamental frequency = n =?
Solution:
Fundamental frequency of vibration is given by

Ans: Fundamental frequency = 698.3 Hz
Example 16:
A metal wire of length 10√10 cm and radius 0.5 mm is stretched by a load of 3.14 kg. The density of material of the wire is 9.8 g cm-3. Find the fundamental frequency of vibrations of the wire. g = 9.8m s-2.
Given: Vibrating length = l = 10√10 cm = 10√10 x 10-2 m, Radius of wire = d = 0.5 mm = 0.5 x 10-3 m, Density of material of wire = ρ = 9.8 g cm-3=9.8 x 103 kg m-3, Tension = 3.14 kg-wt = 3.14 x 9.8 N.
To Find: Fundamental frequency = n =?
Solution:
Diameter of string = 2 r = 2 x0.5 x 10-3 m = 1 x 10-3 m
Fundamental frequency of vibration is given by

Ans: Fundamental frequency of vibration = 100 Hz