Science > Physics > Electrostatics > Mechanical force per Unit Area of Charge Conductor
In this article, we shall study the cause of mechanical force acting on a charged conductor and hence shall derive an expression for mechanical force per unit area of the conductor.
Expression for Mechanical Force per Unit Area of a Charged Conductor:
Every element of a charged conductor experiences a normal outward mechanical force. This is the result of repulsive force from similar charges present on the rest of the surface of the conductor.
Consider a small element, dS on the surface of a charged conductor. If σ is the surface charge density and the charge carried by the element dS be dq.
dq = σ .dS ….(1)
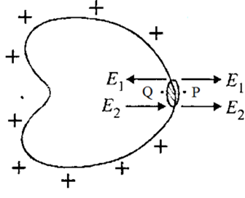
Consider a point P just outside the surface near the element dS. The electric intensity at a point P is given by
E = σ /εok ….(2)
The direction of the intensity is normally outwards.

Now, consider a point Q inside the conductor very near to element dS.

Here E2 is the electric intensity due to the charge on the rest of the conductor. Hence repulsive force experienced by element dS carrying charge dq due to is given by

This is the mechanical force over dS area of a charged conductor. S.I. unit of force per unit area is N/m².
Expression for Energy per Unit Volume (Energy Density) of a Medium:
During the process of charging a conductor, work has to be done to bring a charge on the surface of the conductor. This work is stored in the electric field surrounding the conductor in the form of electrostatic energy. A charged conductor is in an electric field.
The mechanical force acting on it over dS area is given by

The force is directed normally outwards.

Under the action of force, of the element dS moves outward through a distance dl, then the work done by the force is given by,

The work done dW is stored in the medium as electric potential energy dU. i.e. dW = dU. Then the energy per unit volume or energy density is given by

This is an expression for energy per unit volume (energy density) of a medium. Its S.I. unit is joule per cubic metre (J/m³)
Note:

Previous Topic: Numerical Problems on Electrical Intensity Due to Charged Sphere
Next Topic: Dielectrics (Dielectric Materials)