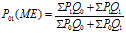Marshall Edgeworth Method

Management > Managerial Statistics > Index Number By Marshall Edgeworth Method

The Marshall Edgeworth Method for the index number, credited to Marshall (1887) and Edgeworth (1925), is a weighted relative of the current period to base period sets of prices. This index uses the arithmetic average of the current and based period quantities for weighting.

Price Index by Marshall Edgeworth Method:

Steps involved:

1. Denote prices of the commodity in the current year as P1 its quantity consumed in that year by Q1.
2. Denote prices of the commodity in the base year as P0 and its quantity consumed in that year by Q0.
3. Find the quantities P0Q0, P1Q0, P0Q1, and p1Q1 for each commodity.
4. Find the sum of each column of P0Q0, P1Q0 , P0Q1, and p1Q1 denote the sums by ∑ P0Q0, ∑ P1Q0, ∑ P0Q1, and ∑ P1Q1 respectively.
5. Use following formula to calculate the index number by Marshall Edgeworth Method.

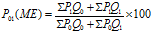
Example – 01:

Compute Price index by Marshall Edgeworth Method from the following data.

Commodity	Base Year		Current Year
	Price	Quantity	Price	Quantity
A	3	25	5	28
B	1	50	3	60
C	2	30	1	30
D	5	15	6	12

Solution:

Commodity	Base Year		Current Year
	P0	Q0	P1	Q1	P0Q0	P1Q0	P0Q1	P1Q1
A	3	25	5	28	75	125	84	140
B	1	50	3	60	50	150	60	180
C	2	30	1	30	60	30	60	30
D	5	15	6	12	75	90	60	72
Total					∑P0Q0=260	∑P1Q0=395	∑P0Q1=264	∑P1Q1=422

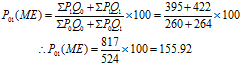
Marshall Edgeworth price index is 155.92

Quantity Index by Marshall Edgeworth Method:

Steps involved:

1. Denote prices of the commodity in the current year as P1 its quantity consumed in that year by Q1.
2. Denote prices of the commodity in the base year as P0 and its quantity consumed in that year by Q0.
3. Find the quantities P0Q0, P1Q0, P0Q1, and p1Q1 for each commodity.
   Find the sum of each column of P0Q0, P1Q0 , P0Q1, and p1Q1 denote the sums by ∑ P0Q0, ∑ P1Q0, ∑ P0Q1, and ∑ P1Q1 respectively.
4. Use the following formula to find Marshall Edgeworth index number.

Example – 02:

Compute Price index by Marshall Edgeworth Method from the following data.

Commodity	Base Year		Current Year
	Price	Quantity	Price	Quantity
A	3	25	5	28
B	1	50	3	60
C	2	30	1	30
D	5	15	6	12

Commodity	Base Year		Current Year
	P0	Q0	P1	Q1	Q0P0	Q1P0	Q0P1	Q1P1
A	3	25	5	28	75	84	125	140
B	1	50	3	60	50	60	150	180
C	2	30	1	30	60	60	30	30
D	5	15	6	12	75	60	90	72
Total					∑P0Q0=260	∑P1Q0=264	∑P0Q1=395	∑P1Q1=422

Marshall Edgworth quantity index is 104.73

Previous Topic: Fisher’s Ideal Index Number

Next Topic: Kelly’s Method

Management > Managerial Statistics > Index Number By Marshall Edgeworth Method