Science > Chemistry > Atomic Structure > Heisenberg’s Uncertainty Principle
In this article, we shall study Heisenberg’s uncertainty principle, the concept of quantum numbers, and the model of an atom based on the quantum numbers.
Heisenberg’s Uncertainty Principle:
Werner Heisenberg a German physicist in 1927, stated the uncertainty principle which is the consequence of dual behaviour of matter and radiation. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron. Mathematically, it can be given as
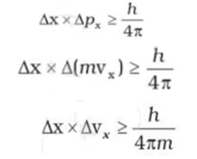
Where Δx is the uncertainty in position, Δp is the uncertainty in momentum and Δv is the uncertainty in velocity of the particle.
If the position of the electron is known with a high degree of accuracy (Δx is small), then the velocity of the electron will be
uncertain [Δ(vx) is large]. On the other hand, if the velocity of the electron is known precisely (Δ(vx ) is small), then the
position of the electron will be uncertain (Δx will be large).
Thus, if we carry out some physical measurements on the electron’s position or velocity, the outcome will always depict a
fuzzy or blur picture.
Notes:
The uncertainty principle can be best understood with the help of an example. Suppose you are asked to measure the thickness of a sheet of paper with an unmarked metre scale. Obviously, the results obtained would be extremely inaccurate and meaningless. In order to obtain any accuracy, you should use an instrument graduated in units smaller than the thickness of a sheet of paper. Analogously, in order to determine the position of an electron, we must use a scale calibrated in units of smaller than the dimensions of the electron ( the electron is considered as a point charge).
To observe an electron, we can illuminate it with “light” or electromagnetic radiation. The “light” used must have a wavelength smaller than the dimensions of an electron. The high momentum photons of such light would change the energy of electrons by collisions. In this process, we, no doubt, would be able to calculate the position of the electron, but we would know very little about the velocity of the electron after the collision.
Significance of Uncertainty Principle:
One of the important implications of the Heisenberg Uncertainty Principle is that it rules out existence of definite paths or
trajectories of electrons and other similar particles.
The trajectory of an object is determined by its location and velocity at various moments. If we know where a body is at a
particular instant and if we also know its velocity and the forces acting on it at that instant, we can tell where the body would
be sometime later. We, therefore, conclude that the position of an object and its velocity fix its trajectory.
Since for a subatomic object such as an electron, it is not possible simultaneously to determine the position and velocity at
any given instant to an arbitrary degree of precision, it is not possible to talk about the trajectory of an electron.
The effect of Heisenberg Uncertainty Principle is significant only for the motion of microscopic objects and is negligible for that of macroscopic objects.
Thus the classical picture of electrons moving in Bohr’s orbits (fixed) cannot hold good. It, therefore, means that the precise statements of the position and momentum of electrons have to be replaced by the statements of probability, that the electron has at a given position and momentum. This is what happens in the quantum mechanical model of an atom.
Schrodinger’s Wave Equation:
Schrodinger independently studied the nature of electron and gave equation which is known as Schrodinger wave equation.
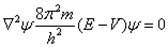
Where, E = Total energy of the system
V = Potential energy of the system
m = Mass of electron
h = Planck’s constant
∇ = Operator
ψ = Wave function and is the amplitude of the electron wave.
ψ 2 gives the probability of finding the electron at various places in a given region of space to another. Thus probabilities of finding the electron in different regions are different. This is in accordance with uncertainity principle.
The acceptable values of wave functions provide the regions around the nucleus in which probability of finding the electron is
maximum. These regions are called orbitals. Thus solving Schrodinger wave equation we can get the shape of the orbitals.This equation also gives certain specific numbers called quantum numbers which specify the location of an electron in an atom.
Concept of Orbitals:
The classical picture of electrons moving in Bohr’s orbits (fixed) cannot hold good. It, therefore, means that the precise statements of the position and momentum of electrons have to be replaced by the statements of probability, that the electron has at a given position and momentum. This is what happens in the quantum mechanical model of an atom.
After solving Schrodinger wave equation, the acceptable values of wave functions provide the regions around the nucleus in which probability of finding the electron is maximum. These regions are called orbitals. Thus solving Schrodinger wave equation we can get the shape of the orbitals.
- Thus electron is a cloud of negative charge with different shapes.
- The three-dimensional region in the space around the nucleus in which the probability of finding the electron is maximum is called orbital.
- In each orbital, the electron has a definite energy. The energy of an orbital is lower if it is concentrated near the nucleus.
- It is to be noted that orbital is not same as that of orbit.
There are four types of orbitals known to us till now, they are s, p, d and f orbitals