Science > Chemistry > Atomic Structure > Quantum Numbers and Shapes of Orbitals
In this article, we shall study the concept of quantum numbers and different types of orbitals and their shapes.
Difference Between Shell, Subshell, and Orbital:
- All electrons that have the same value for n (the principal quantum number) are in the same shell.Within a shell (same n), all electrons that share the same (the angular momentum quantum number, or orbital shape) are in the same subshell. The electrons in subshell have same principal quantum number, same azimuthal quantum number and differ in magnetic and spin quantum number
- When electrons share the same n, l, and m, we say they are in the same orbital (they have the same energy level, shape, and orientation). The electrons in orbital differ only in spin quantum number.
Shapes of Orbitals:
- Node: There is a region where the probability of finding the electron is zero. It is called a node.
- Nodal Plane: A plane passing through the nucleus on which the probability of finding an electron is zero is called the nodal plane. The number of nodal planes in an orbital is equal to the azimuthal quantum number.
- Spherical or Radial Node: A spherical surface within an orbital on which the probability of finding the electron is zero is called a spherical or radial node.
Types of Orbitals:
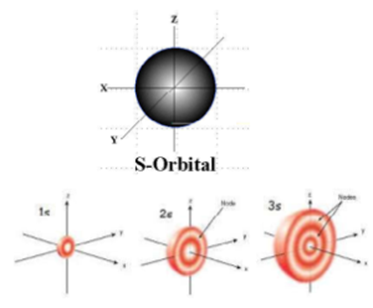
s – orbital:
- For s orbital Azimuthal quantum number = 0 and the magnetic quantum number m = 0 hence s orbitals have unique orientation in space. Thus s orbital corresponds to spherical shape with the atomic nucleus at its centre.
- For every value of ‘n’, there is one ‘s’ orbital i.e. s orbitals are present in all principal energy levels. Its radius depends on the value of n. As the value of n increases the size of the s orbital also increases.
- It has no nodal plane.
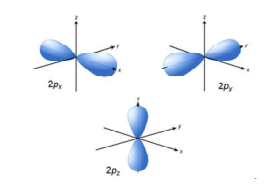
p – orbital:
- For p orbital Azimuthal quantum number l = 1 and the magnetic quantum number m = -1, 0, +1. Hence p orbitals have three orientations in space.
- Thus p orbital corresponds to dumb-belled shape with the atomic nucleus at its center.
- p orbitals have two lobes directed on opposite sides of the nucleus. P-orbitals are orientated in three different directions along X, Y and Z axis of the usual coordinate system. These orbitals are designated as Px, Py & Pz orbitals.
- p-orbital have one nodal plane.
d – orbital:
- For d orbital Azimuthal quantum number l = 2 and the magnetic quantum number m = -2, -1, 0, +1, +2. Hence d orbitals have five orientations in space.
- Thus d orbital corresponds to 4 double dumb-belled shapes (dxy, dyz, dzx, dx2y2) with the atomic nucleus at its centre and one dumb belled with dough nut shaped (dz2).
- d orbital has two nodal planes.

f – orbital:
- For f orbital Azimuthal quantum number l = 3 and the magnetic quantum number m = -3. -2, -1, 0, +1, +2, +3. Hence f orbitals have seven orientations in space.
- f orbital has complex shapes with the atomic nucleus at its centre.
- f orbital has three nodal planes.

Quantum Numbers of Electrons in First Three Shells (Orbits)
| Orbit or Shell No. | Principal Quantum Number n | Azimuthal Quantum Number l | Magnetic Quantum Number m | Spin Quantum Number s | Type Of Orbital |
| 1 | 1 | 0 | 0 | + 1/2 | s Orbital |
| 1 | 1 | 0 | 0 | – 1/2 | s Orbital |
| 2 | 2 | 0 | 0 | + 1/2 | s Orbital |
| 2 | 2 | 0 | 0 | – 1/2 | s Orbital |
| 2 | 2 | 1 | -1 | + 1/2 | px Orbital |
| 2 | 2 | 1 | -1 | – 1/2 | px Orbital |
| 2 | 2 | 1 | 0 | + 1/2 | py Orbital |
| 2 | 2 | 1 | 0 | – 1/2 | py Orbital |
| 2 | 2 | 1 | +1 | + 1/2 | pz Orbital |
| 2 | 2 | 1 | +1 | – 1/2 | pz Orbital |
| 3 | 3 | 0 | 0 | + 1/2 | s Orbital |
| 3 | 3 | 0 | 0 | – 1/2 | s Orbital |
| 3 | 3 | 1 | -1 | + 1/2 | s Orbital |
| 3 | 3 | 1 | -1 | – 1/2 | s Orbital |
| 3 | 3 | 1 | 0 | + 1/2 | px Orbital |
| 3 | 3 | 1 | 0 | – 1/2 | px Orbital |
| 3 | 3 | 1 | +1 | + 1/2 | py Orbital |
| 3 | 3 | 1 | +1 | – 1/2 | py Orbital |
| 3 | 3 | 2 | -2 | + 1/2 | d Orbital |
| 3 | 3 | 2 | -2 | – 1/2 | d Orbital |
| 3 | 3 | 2 | -1 | + 1/2 | d Orbital |
| 3 | 3 | 2 | -1 | – 1/2 | d Orbital |
| 3 | 3 | 2 | 0 | + 1/2 | d Orbital |
| 3 | 3 | 2 | 0 | – 1/2 | d Orbital |
| 3 | 3 | 2 | +1 | + 1/2 | d Orbital |
| 3 | 3 | 2 | +1 | – 1/2 | d Orbital |
| 3 | 3 | 2 | +2 | + 1/2 | d Orbital |
| 3 | 3 | 2 | +2 | – 1/2 | d Orbital |
4 replies on “Quantum Numbers and Shapes of Orbitals”
I must say that this is perfect
Well done!
This is great
Fantastic!!