Quantum Numbers and Quantum Model of an Atom

Science > Chemistry > Atomic Structure > Quantum Numbers and Quantum Model of an Atom

In this article, we shall study the concept of quantum numbers and the model of an atom based on the quantum numbers.

Concept of Quantum Numbers:

In 1926, Erwin Schrodinger put forward a theory of atom called as a quantum mechanical theory. Quantum mechanical theory is based on two principles. a) Wave-particle duality of subatomic particles and b) Uncertainty principle.

Wave-particle duality principle of subatomic particles was put forward by L. DeBroglie it states that “All the subatomic particles electrons, protons, and neutrons possess both particle and wave properties”.

Uncertainty principle was put forward by W. Heisenberg it states that “It is impossible to determine the position and momentum of a particle simultaneously”. It means that if the position of the electron in an atom is known then there is uncertainty about its momentum and when the momentum of an electron in an atom is known there is uncertainty about the position of the electron.

According to this theory, Each electron shell of an atom is composed of several subshells. To specify the position of the electron in an atom each electron is assigned four quantum numbers and these numbers give location and energy of the electron.

The numbers which assign the position and energy to an electron are called quantum numbers. There is a set of four quantum numbers associated with each electron of an atom. The four quantum numbers are a) Principal quantum number ‘n’  b) Azimuthal quantum number ‘l’ c) Magnetic quantum number ‘m’  d) Spin quantum number ‘s’

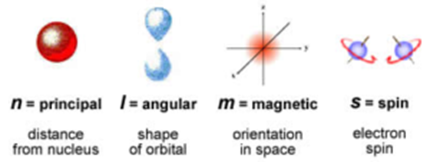
Principal Quantum Number (n):

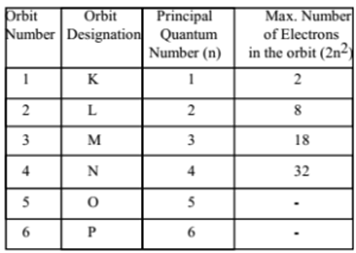
This quantum number was introduced by Neil Bohr. It is denoted by the letter ‘n’. It gives the main energy level (shell) to which the electron belongs. It defines the distance of the electron from the nucleus and energy level. These energy levels are also designated by letters as follows:

Azimuthal Quantum Number (l):

It was introduced by Somerfield.  This quantum number refers to the energy sub-level (subshell).  It is denoted by the letter ‘l’. It can have any integral value from 0 to (n – 1). This quantum number indicates the subshell in which the electron is present and the number of subshells present in a principal shell.

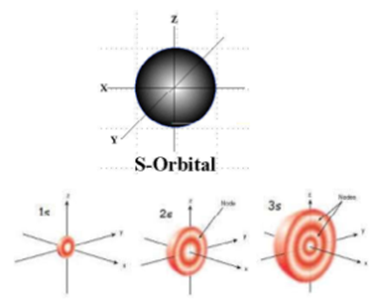
It is also responsible for the particular shape of the particular shell because it defines the spatial distribution of the electron cloud around the nucleus. Thus the subshell (Orbital) with l = 0 is called ‘s’ orbital. The subshell (Orbital) with l = 1 is called ‘p’ orbital. The subshell (Orbital) with l = 2 is called ‘d’ orbital. The subshell (Orbital) with l = 3  is called ‘f’ orbital

It is used to calculate angular momentum of an electron in particular shell using the formula

Each subshell contains maximum 2 (2l +1) electrons. It also decides the number of nodal planes of the orbital. For s orbital l = 0, hence s orbital there is no nodal plane. For p orbital l = 1, hence p orbital there is one nodal plane. For d orbital l = 2, hence d orbital there are two nodal planes.

Notes:

For the first orbit:

n = 1, then  l = 0 to (1 – 1) = 0 to 0,  then  l = 0. Thus in the first main energy level, there is only one subshell i.e. ‘s’ orbital.

For the second orbit:

n = 2 then  l = 0 to (2 – 1) = 0 to 1, then l = 0, 1. Thus in the second main energy level, there are two subshells i.e. ‘s’ orbital and ‘p’ orbital.For the Third orbit n = 3 Then  = 0 to (3 – 1) = 0 to 2 then             = 0, 1, 2. Thus in the third main energy level there

For the Third orbit:

n = 3 then  l = 0 to (3 – 1) = 0 to 2 then l = 0, 1, 2. Thus in the third main energy level, there are three subshells i.e. ‘s’ orbital, ‘p’ orbital and ‘d’ orbital.

For the fourth orbit:

n = 4 Then l = 0 to (4 – 1) = 0 to 3 then l  = 0, 1, 2, 3. Thus in the fourth main energy level, there are four subshells i.e. ‘s’ orbital, ‘p’ orbital, ‘d’ orbital, and ‘f’ orbital.

Magnetic Quantum Number (m):

This quqntum number is denoted by letter ‘m’. This number was introduced to explain the splitting of atomic spectra in a magnetic field (Zeeman effect).

For Azimuthal number ‘l’ possible values of magnetic quantum numbers are – l  to + l   through 0. i.e. m =  , …., -3, -2, -1, 0, 1, 2, 3, ….., . This quantum number gives the possible orientation of the orbital in the space. For a given value of l, there are (2l +1) values of m.

This number is also known as the orientation quantum number because it gives the distribution of electron clouds in space around the nucleus.

The magnetic quantum number tells to which orbital the electron belongs. It also tells the number of orbitals which corresponds to a particular shell. For example: s subshell l = 0 therefore m = 0. This means that s subshell contains only one orbital.

p subshell l = 1 therefore m = -1, 0, +1. This means that p subshell contains three orbitals. They are designated as Px, Py and Pz,  along the x-axis, along the y-axis and along the z-axis respectively. Thus p orbitals have three orientations in space along co-ordinate axes. In absence of magnetic field, these orbitals are equivalent in energy and are said to have three fold degenerate.

d subshell l = 2 therefore m = -2, -1, 0, +1, +2. This means that d subshell contains five orbitals. They are designated as dxy, dyz, dzx, dx2-y2, and dz2.   Thus d orbitals have five orientations in space. In absence of magnetic field, these orbitals are equivalent in energy and are said to have five fold degenerate.

f subshell l = 3 therefore m = -3, -2, -1, 0, +1, +2, +3. This means that f subshell contains seven orbitals and have seven orientations in space. In absence of magnetic field, these orbitals are equivalent in energy and are said to have seven fold degenerate.

Spin Quantum Number (s):

It is denoted by letter ‘s’. The electron in orbital motion can spin clockwise or anticlockwise about its own axis, hence two values of quantum number are possible.  These values are taken as + 1/2 and – 1/2.

Opposite spins are called antiparallel spins. The same spin is called the parallel spin. The spin quantum number indicates a magnetic moment associated with the electron.

Science > Chemistry > Atomic Structure > Quantum Numbers and Quantum Model of an Atom