Science > Mathematics > Statistics and Probability > Probability > Checking of Probability Mass Function
In this article, we shall study to check whether the given function is a probability mass function or not.
Example – 01:
| X = x | 1 | 2 | 3 | 4 |
| P(X=x) | 0.1 | 0.2 | 0.3 | 0.4 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, 1 ≤ x ≤ 4) = P(1) + P(2) + P(3) + P(4)
∴ ∑ P(X = x, 1 ≤ x ≤ 4) = 0.1 + 0.2 + ).3 + 0.4 = 1
Thus sum of all probabilities is 1. Hence the second condition is satisfied.
Hence given function is a p.m.f.
Example – 02:
| X = x | 0 | 1 | 2 | 3 |
| P(X=x) | 0.5 | 0.2 | 0.18 | 0.12 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, 0 ≤ x ≤ 3) = P(0) + P(1) + P(2) + P(3)
∴ ∑ P(X = x, 0 ≤ x ≤ 3) = 0.5 + 0.2 + 0.18 + 0.12 = 1
Thus sum of all probabilities is 1. Hence the second condition is satisfied.
Hence given function is a p.m.f.
Example – 03:
| X = x | -1 | 0 | 1 |
| P(X=x) | – 0.2 | 1 | 0.2 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that P(-1) = – 0.2 < 0 Hence the first condition is not satisfied.
Hence given function is not a p.m.f.
Example – 04:
| X = x | 0 | 1 | 2 |
| P(X=x) | 0.6 | 0.1 | 0.2 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, 0 ≤ x ≤ 1 = P(0) + P(1) + P(2)
∴ ∑ P(X = x, 0 ≤ x ≤ 2) = 0.6 + 0.1 + 0.2 = 0.9 ≠ 1
Thus sum of all probabilities is not equal to1. Hence the second condition is not satisfied.
Hence given function is not a p.m.f.
Example – 05:
| X = x | 2 | 4 | 6 | 8 |
| P(X=x) | 0.2 | 0.4 | 0.6 | 0.8 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, x = 2, 4, 6, 8) = P(2) + P(4) + P(6) + P(8)
∴ ∑ P(X = x, x = 2, 4, 6, 8) = 0.2 + 0.4 + 0.6 + 0.8 = 2 ≠ 1
Thus sum of all probabilities is not equal to 1. Hence the second condition is not satisfied.
Hence given function is not a p.m.f.
Example – 06:
| X = x | -2 | -1 | 1 | 2 |
| P(X=x) | 0.5 | -0.1 | 0.6 | 0 |
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that P(-1) = – 0.1 < 0 Hence the first condition is not satisfied.
Hence given function is not a p.m.f.
Example – 07:
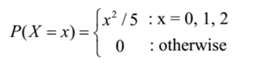
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
∴ P(X = 0) = 02/5 = 0/5 = 0
∴ P(X = 1) = 12/5 = 1/5
∴ P(X = 2) = 22/5 = 4/5
The probability distribution is
| X = x | 0 | 1 | 2 |
| P(X=x) | 0 | 1/5 | 4/5 |
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, x = 0, 1, 2) = P(0) + P(1) + P(2)
∴ ∑ P(X = x, x = 0, 1, 2) = 0 + 1/5 + 4/5 = 5/5 = 1
Thus sum of all probabilities is 1. Hence the second condition is satisfied.
Hence given function is a p.m.f.
Example – 08:

Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
∴ P(X = 0) = (1- 1)/3 = 0/3 = 0
∴ P(X = 1) = (2 – 1)/3 = 1/3
∴ P(X = 2) = (3 – 1)/3 = 2/3
The probability distribution is
| X = x | 1 | 2 | 3 |
| P(X=x) | 0 | 1/3 | 2/3 |
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, x = 1, 2, 3) = P(1) + P(2) + P(3)
∴ ∑ P(X = x, x = 1, 2, 3) = 0 + 1/3 + 2/3 = 1
Thus sum of all probabilities is 1. Hence the second condition is satisfied.
Hence given function is a p.m.f.
Example – 09:
The function is P( X = x) = (x – 5)/4, x = 5.5, 6.5, 7.5
Verify whether the function can be regarded as a probability mass function (p.m.f.)
Solution:
∴ P(X = 5.5) = (5.5 – 5)/4 = 0.5/4 = 1/8
∴ P(X = 6.5) = (6.5 – 5)/4 = 1.5/4 = 3/8
∴ P(X = 7.5) = (7.5 – 5)/4 = 2.5/4 = 5/8
The probability distribution is
| X = x | 5.5 | 6.5 | 7.5 |
| P(X=x) | 1/8 | 3/8 | 5/8 |
Checking of the first condition (P(X = x) ≥ 0, ∀ x)
We can see that all the values of P(X = x) ≥ 0. Hence the first condition is satisfied.
Checking of the second condition ∑ P(X = x) = 1
∑ P(X = x, x = 5.5, 6.5, 7.5) = P(5.5) + P(6.5) + P(7.5)
∴ ∑ P(X = x, x = 5.5, 6.5, 7.5) = 1/8 + 3/8 + 5/8 = 9/8 ≠ 1
Thus sum of all probabilities is not equal to 1. Hence the second condition is not satisfied.
Hence given function is not a p.m.f.