Science > Mathematics > Trigonometry > Angle Measurement > Measurement of Angle in Radians
In this article, we shall study to find a measure of an angle in radians and degrees.
Express following angles in degrees, minutes, and seconds
Degrees x 60 = Minutes
Minutes x 60 = Seconds
- 74.87°
74.87° = 74° + 0.87°
∴ 74.87° = 74° + 0.87 x 60′
∴ 74.87° = 74° + 52.2′
∴ 74.87° = 74° + 52′ + 0.2′
∴ 74.87° = 74° + 52′ + 0.2 x 60”
∴ 74.87° = 74° + 52′ + 12”
∴ 74.87° = 74°,52′,12”
- – 30.6947°
– 30.6947° = – (30° + 0.6947°)
∴ – 30.6947° = – (30° + 0.6947 x 60′)
∴ – 30.6947° = – (30° + 41.682′)
∴ – 30.6947° = – (30° + 41′ + 0.682′)
∴ – 30.6947° = – (30° + 41′ + 0.682 x 60”)
∴ – 30.6947° = – (30° + 41′ + 40.92”)
∴ – 30.6947° = – (30° + 41′ + 41”)
∴ – 30.6947° = – 30°,41′,41” approx.
- 321.9°
321.9° = 321° + 0.9°
∴ 321.9° = 321° + 0.9 x 60′
∴ 321.9° = 321° + 54′
∴ 321.9° = 321°,54′,0”
- 200.6°
200.6° = 200° + 0.6°
∴ 200.6° = 200° + 0.6 x 60′
∴ 200.6° = 200° + 36′
∴ 200.6° = 200°,36′,0”
- 11.0133°
11.0133° = 11° + 0.0133°
∴ 11.0133° = 11° + 0.0133 x 60′
∴ 11.0133° = 11° + 0.798′
∴ 11.0133° = 11° + 0′ + 0.798′
∴ 11.0133° = 11° + 0′ + 0.798 x 60”
∴ 11.0133° = 11° + 0′ + 47.88”
∴ 11.0133° = 11° + 0′ + 48”
∴ 11.0133° = 11°,48” approx.
- 94.3366°
94.3366° = 94° + 0.3366°
∴ 94.3366° = 94° + 0.3366 x 60′
∴ 94.3366° = 94° + 20.196′
∴ 94.3366° = 94° + 20′ + 0.196′
∴ 94.3366° = 94° + 20′ + 0.196 x 60”
∴ 94.3366° = 94° + 20′ + 11.76”
∴ 94.3366° = 94° + 20′ + 12”
∴ 11.0133° = 94°,20′,12” approx.
Conversion of Angles in Degrees into Radians
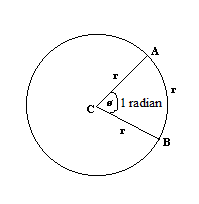
Degrees x π/180 = Radians
| Sr. No. | Angle in degrees | Conversion | Angle in radians |
| 1 | 30° | 30 x π/180 | (π/6)c |
| 2 | 45° | 45 x π/180 | (π/4)c |
| 3 | 60° | 60 x π/180 | (π/3)c |
| 4 | 90° | 90 x π/180 | (π/2)c |
| 5 | 120° | 120 x π/180 | (2π/3)c |
| 6 | 135° | 135 x π/180 | (3π/4)c |
| 7 | 180° | 180 x π/180 | (π)c |
| 8 | 75° | 75 x π/180 | (5π/12)c |
| 9 | -270° | – 270 x π/180 | – (3π/2)c |
| 10 | – (1/3)° | – (1/3) x π/180 | – (π/540)c |
| 11 | 225° | 225 x π/180 | (5π/4)c |
| 12 | 945° | 945 x π/180 | (21π/4)c |
| 13 | – 600° | – 600 x π/180 | – (10π/3)c |
| 14 | – (1/5)° | – (1/5) x π/180 | (π/900)c |
| 15 | -108° | – 108 x π/180 | – (3π/5)c |
| 16 | – 144° | -144 x π/180 | -(4π/5)c |
Conversion of Angles in Radians into Degrees
Radians x 180/π = Degrees
| Sr. No. | Angle in radians | Conversion | Angle in degrees |
| 1 | (π/6)c | (π/6) x (180/π) | 30° |
| 2 | (π/4)c | (π/4) x (180/π) | 45° |
| 3 | (π/3)c | (π/3) x (180/π) | 60° |
| 4 | (π/2)c | (π/2) x (180/π) | 90° |
| 5 | (3π/2)c | (3π/2) x (180/π) | 120° |
| 6 | (3π/4)c | (3π/4) x (180/π) | 135° |
| 7 | (π)c | (π) x (180/π) | 180° |
| 8 | (7π/8)c | (7π/8)x (180/π) | 157.5° |
| 9 | – (9π/2)c | – (9π/2) x (180/π) | – 810° |
| 10 | (4.4)c | (4.4) x (180/π) | 252° |
| 11 | (5π/12)c | (5π/12) x (180/π) | 75° |
| 12 | – (7π/12)c | -(7π/12) x (180/π) | -105° |
| 13 | 8c | 8 x (180/π) | (1440/π)° |
| 14 | (1/3)c | (1/3) x (180/π) | (60/π)° |
| 15 | (5π/7)c | (5π/7) x (180/π) | (900/7π)° |
| 16 | -(2π/9)c | -(2π/9) x (180/π) | – 40° |
| 17 | – (7π/24)c | – (7π/24) x (180/π) | – 52.5° |
Problems Based on Degree and Radian Measures of Angles:
Example – 01:
The difference between the two acute angles of a right-angle triangle is (2π/5)c. Find the angles in degrees.
Solution:
Let the two acute angles be x and y in degrees
Given their difference is (2π/5)c.= (2π/5) x (180/π) = 72°
∴ x – y = 72° ……… (1)
Now the sum of acute angles of triangle is always 90°
∴ x + y = 90° ……… (2)
Solving equation (1) and (2) we get
x = 81° and y = 9°
Ans: The acute angles of triangle are 81° and 9°
Example – 02:
The difference between the two acute angles of a right-angled triangle is (3π/10)c. Find the angles in degrees.
Solution:
Let the two acute angles be x and y in degrees
Given their difference is (3π/10)c.= (3π/10) x (180/π) = 54°
∴ x – y = 54° ……… (1)
Now the sum of acute angles of triangle is always 90°
∴ x + y = 90° ……… (2)
Solving equation (1) and (2) we get
x = 72° and y = 18°
Ans: The acute angles of triangle are 72° and 18°
Example – 03:
The sum of the two angles is 5πc and their difference is 60°. Find the angles in degrees.
Solution:
Let the two acute angles be x and y in degrees
Given their sum is 5πc.= (5π) x (180/π) = 900°
∴ x + y = 900° ……… (1)
Given their differene is 60°
∴ x – y = 60° ……… (2)
Solving equation (1) and (2) we get
x = 480° and y = 420°
Ans: The acute angles of triangle are 480° and 420°
Example – 04:
The measures of angles of a triangle are in the ratio 2:3:5. Find their measures in radians.
Solution:
The angles.of triangle are in the ratio 2:3:5
Let the three angles be 2k, 3k, and 5k.
Now the sum of all angles of triangle is 180°
∴ 2k + 3k + 5k = 180°
∴ 10k = 180°
∴ k = 18°
∴ The three angles are ( 2 x 18° = 36°), (3 x 18° = 54°), and (5 x 18°) = 90°
36° = 36 x π/180 = (π/5)c
54° = 54 x π/180 = (3π/10)c
90° = 90 x π/180 = (π/2)c
Ans: The angles of quadrilateral are (π/5)c, (3π/10)c, and (π/2)c,
Example – 05:
One angle of a triangle is (2π/9)c and the measures of the other two angles.are in the ratio 4:3. Find their measures in degrees and radians.
Solution:
one of the angle of triangle is of measure (2π/9)c .= (2π/9) x (180/π) = 40°
other two angles.are in the ratio 4:3
Let the two angles be 4k, and 3k.
Now the sum of all angles of triangle is 180°
∴ 4k + 3k + 40° = 180°
∴ 7k = 140°
∴ k = 20°
∴ The two angles are ( 4 x 20° = 80°) and (3 x 20° = 60°)
80° = 80 x π/180 = (4π/9)c
60° = 60 x π/180 = (π/3)c
Ans: The two angles of triangle are 80° and 60° or (4π/9)c and (π/3)c,
Example – 06:
In ΔABC, m∠A = (2π/3)c and m∠B = 45°. Find m∠C in both the system.
Solution:
m∠A = (2π/3)c = (2π/3) x (180/π) = 120°
Now the sum of all angles of triangle is 180°
m∠A + m∠B + m∠C = 180°
∴ 120° + 45° + m∠C = 180°
∴ m∠C = 180° – 165°
∴ m∠C = 15° = 15 x (π /180) = (π/12)c
Ans: m∠C = 15° or (π/12)c
Example – 07:
If the radian measures of two angles of a triangle are (5π/9)c and (5π/18)c. Find the measure of the third angle in radians and degrees.
Solution:
Let m∠A = (5π/9)c = (5π/9) x (180/π) = 100°
Let m∠B = (5π/18)c = (5π/18) x (180/π) = 50°
Now the sum of all angles of triangle is 180°
m∠A + m∠B + m∠C = 180°
∴ 100° + 50° + m∠C = 180°
∴ m∠C = 180° – 150°
∴ m∠C = 30° = 30 x (π /180) = (π/6)c
Ans: Measure of third angle is (π/6)c or 30°
Example – 08:
If the radian measures of two angles of a triangle are (3π/5)c and (4π/15)c. Find the measure of the third angle in radians and degrees.
Solution:
Let m∠A = (3π/5)c = (3π/5) x (180/π) = 108°
Let m∠B = (4π/15)c = (4π/15) x (180/π) = 48°
Now the sum of all angles of triangle is 180°
m∠A + m∠B + m∠C = 180°
∴ 108° + 48° + m∠C = 180°
∴ m∠C = 180° – 156°
∴ m∠C = 24° = 24 x (π /180) = (2π/15)c
Ans: Measure of third angle is (2π/15)c or 24°
Example – 09:
In ΔLMN, m∠L = (3π/4)c and m∠N = 30°. Find m∠M in both the system.
Solution:
m∠L = (3π/4)c = (3π/4) x (180/π) = 135°
Now the sum of all angles of triangle is 180°
m∠L + m∠M + m∠N = 180°
∴ 135° + m∠M + 30° = 180°
∴ m∠M = 180° – 165°
∴ m∠M = 15° = 15 x (π /180) = (π/12)c
Ans: m∠M = 15° or (π/12)c
Example – 10:
One angle of a quadrilateral is (2π/9)c and the measures of the other three angles.are in the ratio 3:5:8. Find their measures in radians.
Solution:
one of the angle of quadrilateral is of measure (2π/9)c .
= (2π/9) x (180/π) = 40°
other three angles.are in the ratio 3:5:8
Let the three angles be 3k, 5k, and 8k.
Now the sum of all angles of quadrilateral is 360°
∴ 3k + 5k + 8k + 40° = 360°
∴ 16k = 320°
∴ k = 20°
∴ The three angles are ( 3 x 20° = 60°), (5 x 20° = 100°), and (8 x 20°) = 160°
60° = 60 x π/180 = (π/3)c
100° = 100 x π/180 = (5π/9)c
160° = 160 x π/180 = (8π/9)c
Ans: The angles of quadrilateral are (2π/9)c, (π/3)c, (5π/9)c, and (8π/9)c,
Example – 11:
One angle of a quadrilateral is (2π/5)c and the measures of the other three angles.are in the ratio 2:3:4. Find their measures in degrees and radians.
Solution:
one of the angle of quadrilateral is of measure (2π/5)c .
= (2π/5) x (180/π) = 72°
other three angles.are in the ratio 2:3:4
Let the three angles be 2k, 3k, and 4k.
Now the sum of all angles of quadrilateral is 360°
∴ 2k + 3k + 4k + 72° = 360°
∴ 9k = 288°
∴ k = 32°
∴ The three angles are ( 2 x 32° = 64°), (3 x 32° = 96°), and (4 x 32°) = 128°
64° = 64 x π/180 = (16π/45)c
96° = 96 x π/180 = (24π/45)c
128° = 108 x π/180 = (32π/4)c
Ans: The angles of quadrilateral are (2π/9)c, (π/3)c, (5π/9)c, and (8π/9)c,
Example – 12:
The measures of angles of a quadrilateral are in the ratio 2:3:6:7. Find their measures in degrees and radians.
Solution:
The measures of angles are in the ratio 2:3:6:7
Let the measures of angles be 2k, 3k, 6k and 7k.
Now the sum of all angles of quadrilateral is 360°
∴ 2k + 3k + 6k + 7k = 360°
∴ 18k = 360°
∴ k = 20
∴ The measures of angles are ( 2 x 20° = 40°), (3 x 20° = 60°), (6 x 20° = 120°), and (7 x 20°) = 140°
40° = 40 x π/180 = (2π/9)c
60° = 60 x π/180 = (π/3)c
120° = 120 x π/180 = (2π/3)c
140° = 140 x π/180 = (7π/9)c
Ans: The measures of angles of quadrilateral are 40°, 60°, 120°, and 140°
or (2π/9)c, (π/3)c, (2π/3)c, and (7π/9)c,
Example – 13:
The measures of angles of a quadrilateral are in the ratio 3:4:5:6. Find their measures in degrees and radians.
Solution:
The measures of angles are in the ratio 3:4:5:
Let the measures of angles be 3k, 4k, 5k and 6k.
Now the sum of all angles of quadrilateral is 360°
∴ 3k + 4k + 5k + 6k = 360°
∴ 18k = 360°
∴ k = 20
∴ The measures of angles are ( 3 x 20° = 60°), (4 x 20° = 80°), (5 x 20° = 100°), and (6 x 20°) = 120°
60° = 60 x π/180 = (π/3)c
80° = 80 x π/180 = (2π/9)c
100° = 100 x π/180 = (5π/9)c
120° = 120 x π/180 = (2π/3)c
Ans: The measures of angles of quadrilateral are 60°, 80°, 100°, and 120°
or (π/3)c, (2π/9)c, (5π/9)c, and (2π/3)c,
Example – 14:
The angles of triangle are in A.P. and the greatest angle is 84°. Find all the three angles in radians.
Solution:
Let the three angles of a triangle in A.P. be (a – d), a, (a + d) in degrees
Now the sum of all angles of a triangle is 180°
(a – d) + a + (a + d) = 180°
∴ 3a = 180°
∴ a = 60° = 60 x π/180 = (π/3)c
Now the greatest angle is 84°
∴ a + d = 84°
∴ 60° + d = 84° = 84 x π/180 = (7π/15)c
∴ d = 24°
∴ a – d = 60° – 24° = 36° = 36 x π/180 = (π/5)c
Ans: Measure of the angleare of triangle are (π/5)c, (π/3)c, (7π/15)c,
Example – 15:
The angles of a quadrilateral are in A.P. and the greatest angle is double the least. Express the least angle in radians.
Solution:
Let the four angles of quadrilateral in A.P. be (a – 3d), (a -d), (a +d), and (a + 3d) in degrees
Now the sum of all angles of quadrilateral is 360°
(a- 3d) + (a – d) + (a + d) + (a + 3d) = 360°
∴ 4a = 360°
∴ a = 90°
Now the greatest angle is double the least
∴ a + 3d = 2(a – 3d)
∴ 90 + 3d = 2(90 – 3d)
∴ 90 + 3d = 180 – 6d
∴ 9d = 90
∴ d = 10°
Least angle = a – 3d = 90° – 3 x 10° = 90° – 30° = 60° = 60 x (π /180) = (π/3)c
Ans: The least angle in radians is (π/3)c.