Science > Physics > Units and Measurements > Applications of Dimensional Analysis
In this article, we shall study the applications of dimensional analysis.
Applications of Dimensional Analysis:
- To check the correctness of physical equation:
- To Find Dimensions of New Physical Quantity:
- To derive the form of a physical equation:
- To derive the relation between different units of different systems of a physical quantity:
To check the correctness of physical equation:
We can check the correctness of the physical equation using the principle of homogeneity. By the principle of homogeneity of dimensions, the dimensions of all the terms on the two sides of an equation must be the same.
Example – 01:
To check the correctness of physical equation, v = u + at, Where ‘u’ is the initial velocity, ‘v’ is the final velocity, ‘a’ is the acceleration and ‘t’ is the time in which the change occurs.
Solution:
Given equation is v = u + at
L.H.S. = v, hence [L.H.S.] = [v] = [L1M0T-1] ………………. (1)
R.H.S = u + at, hence [R.H.S] = [u] + [a][t]
[R.H.S] = [L1M0T-1] + [L1M0T-2][L0M0T1]
[R.H.S] = [L1M0T-1] + [L1M0T-1]
[R.H.S] = [L1M0T-1] ……………. (2)
From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by principle of homogeneity the given equation is dimensionally correct.
Example – 02:
To check the correctness of physical equation, v² = u² + 2as, Where ‘u’ is the initial velocity, ‘v’ is the final velocity, ‘a’ is the acceleration and s is the displacement.
Solution:
Given equation is v² = u² + 2as
L.H.S. = v, hence [L.H.S.] = [v]² = [L1M0T-1]² = [L2M0T-2] ………………. (1)
R.H.S = u² + 2as, hence [R.H.S] = [u]² + [a][s]
[R.H.S] = [L1M0T-1]² + [L1M0T-2][L1M0T0]
[R.H.S] = [L2M0T-2] + [L2M0T-2]
[R.H.S] = [L2M0T-2] ……………. (2)
From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity the given equation is dimensionally correct.
Example – 03:
To check the correctness of physical equation, a = v²/r², Where ‘a’ is the centripetal acceleration of a body performing uniform circular motion along a circle of radius ‘r’ with linear speed ‘v’.
Solution:
Given equation is a = v²/r²
L.H.S. = a, hence [L.H.S.] = [a] = [L1M0T-2] ………………. (1)
R.H.S = v²/r² , hence [R.H.S] = [v]²/[r]²
[R.H.S] = [L1M0T-1]2 / [L1M0T0]²
[R.H.S] = [L2M0T-2] / [L2M0T0]
[R.H.S] = [L0M0T-2] ……………. (2)
From (1) and (2) we have [L.H.S.] ≠ [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally not correct.
To Find Dimensions of New Physical Quantity:
To find the form of a physical equation, we use a physical equation which contains the quantity, whose physical dimensions are to be found. Then the equation is rearranged to find the quantity whose dimensions are to be found is written. Knowing dimensions on the right hand side, dimensions of a physical quantity can be obtained.
Example – 04:
Find dimensions of universal gravitation constant (G).
Solution:
If m1 and m2 are two masses separated by a distance r from each other then the force of gravitation acting between them is given by Newton’s law of gravitation
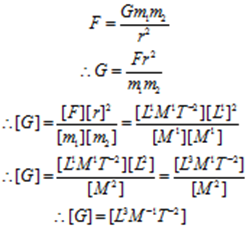
Hence dimensions of universal gravitation constant are [L3M-1T-2]
Example – 05:
Find dimensions of the coefficient of viscosity (η).
Solution:
Le F be the viscous force acting between two layers of liquid area A having velocity difference of dv between them. Let dx be the separation between the two layers and η is coefficient of viscosity, then by Newton’s law of viscosity
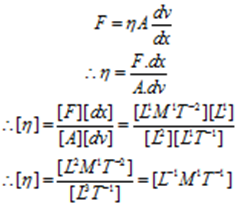
Hence dimensions of the coefficient of viscosity are [L-1M1T-1]
Example – 06:
Find dimensions of electrical permittivity (εo).
Solution:
If q1 and q2 are two masses separated by a distance r from each other then the magnitude of electrostatic force acting between them is given by Coulomb’s law

Hence dimensions of electrical permittivity are [L-3M-1T4I²]
To derive the form of a physical equation:
To find the form of a physical equation, we first consider all the physical quantities on which a given physical quantity is likely to depend. Then, by the application of the principle of homogeneity of dimensions, we eliminate those quantities on which the physical quantity does not depend.
Example – 07:
The period (T) of a simple pendulum is assumed to depend on length (l) of the pendulum, acceleration due to gravity (g) and mass (m) of the bob of the pendulum. If the constant of proportionality is 2π, then find the equation for the time period of the simple pendulum.
Solution:
let T ∝ lx, T ∝ gy, T ∝ mz,
Combining above relations we have T ∝ lx gy mz,
T = k lx gy mz ………….. (1)
By principle of homogeneity of dimensions we have
[T] = [l]x [g]y [m]z
∴ [L0M0T1] = [L1M0T0]x [L1M0T-2]y [L0M1T0]z
∴ [L0M0T1]= [LxM0T0][LyM0T-2y][L0MzT0]
∴ [L0M0T1] = [Lx+y Mz T-2y]
Considering equality of two sides we have
x + y = 0 , z = 0 , -2y = 1
∴ y = -1/2
x + y = 0
∴ x -1/2 = 0
∴ x = 1/2
Substituting x =1/2, y = -1/2 and z = 0 in equation (1) we get
T = k l1/2 g-1/2 m0
T = k l1/2 g-1/2 m0
The value of constant in this case is 2π , i.e. k = 2π

This is the formula for time period of the simple pendulum.
Example – 08:
The centripetal force (F) acting on a body is assumed to depend on the mass (m) of the body, its linear velocity (v) and radius of circular path (r). Show that F ∝ mv²/r
Solution:
let F ∝ mx, F ∝ vy, F ∝ rz,
Combining above relations we have F ∝ mx vy rz,
F = k mx vy rz ………….. (1)
By principle of homogeneity of dimensions we have
[F] = [m]x [v]y [r]z
∴ [L1M1T-2] = [L0M1T0]x [L1M0T-1]y [L1M0T0]z
∴ [L1M1T-2]= [L0MxT0][LyM0T-y][LzM0T0]
∴ [L1M1T-2] = [Ly+z Mx T-y]
Considering equality of two sides we have
y + z = 1 , x = 1 , – y = -2
∴ y = 2
y + z = 1
∴ 2 + z = 1
∴ z = -1
Substituting x =1, y = 2 and z = -1 in equation (1) we get
F = k m1 v2 r-1
∴ F = k. m1 v2 / r
∴ F ∝ mv²/r (Proved as required)
To derive the relation between different units of different systems of a physical quantity:
The dimensional analysis is used to find the conversion factor when the system of units is changed from one type to other.
Example – 09:
Derive the relation between newton (N) and dyne.
Solution:
newton and dyne are units of force in S.I. and c.g.s. system respectively
Dimensions of force are [L1M1T-2]
Example – 10:
Derive the relation between joule (J) and erg.
Solution:
joule and erg are units of energy in S.I. and c.g.s. system respectively
Dimensions of force are [L2M1T-2]
Limitations of Dimensional Analysis:
- The constant of the physical equation cannot be found using dimensional analysis. These constants are to be determined by experiments.
- A physical equation is dimensionally correct does not mean that the equation is scientifically correct.
- It is not useful when the trigonometric or exponential functions are involved.
- This method can be used only for the relations having a product or division relation. It is not used for addition or subtractive relation. Thus it is not used for deriving complex relations.
- This method does not give information about dimensional constant such as Universal gravitation constant G, Planck’s constant h, Rydberg’s constant R, etc.
- In this method, we compare the powers of the fundamental quantities to obtain a number of independent equations for finding the unknown powers. Since the total number of such equations cannot exceed the number of fundamental quantities, we cannot use this method to obtain the relation of the quantity of interest depends upon more parameters than the number of fundamental quantities used.
- In many problems, it is difficult to guess the parameters on which the quantity of interest depends. This requires a trained, subtle, and intuitive mind.
Change of Fundamental Quantities:
Example – 11:
If length ‘L’, force ‘F’ and time ‘T’ are taken as fundamental quantities. What would be the dimensional equation of mass and density?
Solution:
We have Force = Mass × Acceleration
∴ Mass = Force / Acceleration
∴ [Mass] = [Force] / [Acceleration] = [F1]/ [L1T-2] = [F1L-1T2]
Density = Mass / Volume
[Density] = [Mass] / [Volume]= [F1L-1T2] /[L3]= [F1L-4T2]
Dimensions of mass are [F1L-1T2] and that of density are [F1L-4T2]
Example – 13:
If velocity (V), time (T) and force (F) were chosen as fundamental quantities, find dimensions of Mass?
Solution:
We have Force = Mass × Acceleration
∴ Mass = Force / Acceleration
∴ Mass = Force / (Velociy/ time)
∴ Mass = (Force × time) / Velociy
∴ [Mass] = ([Force] × [time]) / [Velociy]
∴ [Mass] = ([F] × [T]) / [V]
∴ [Mass] = [F T V-1]
Dimensions of mass are [F T V-1]
Example – 14:
If the force (F), acceleration (A), and time (T) are taken as fundamental Units, then find the dimensions of energy.
We have Force = Mass × Acceleration
∴ Mass = Force / Acceleration
∴ [Mass] = [F1] / [A1] = [F1A-1]
We have Acceleration = Velociy/ time
∴ Acceleration = (distance/time)/ time
∴ Acceleration = distance/time2
∴ distance = acceleration x time2
∴ [Length] = [Acceleration][time]2 = [AT2]
Now, energy = mass x gravitational acceleration x height
∴ [Energy] = [mass] x [acceleration] x [length]
∴ [Energy] = [F1A-1] x [A-1] x [AT2]
∴ [Energy] = [F1 A-1 T2]
Dimensions of energy are [F1 A-1 T2]
Previous Topic: Dimensions of Physical Quantities
Next Topic: More Problems on Dimensional Analysis

2 replies on “Applications of Dimensional Analysis”
Good work
well done