Bulk Modulus of Elasticity

Science > Physics > Elasticity > Volumetric Stress, Bulk Modulus of Elasticity

In this article, we shall study the concept of volumetric stress, volumetric strain, and bulk modulus of elasticity.

Volumetric stress:

When the deforming forces are such that there is a change in the volume of the body, then the stress produced in the body is called volume stress. e.g. Solid sphere placed in a fluid under high pressure. Mathematically,

Volumetric Stress = Load / Area = Pressure Intensity = dP

S.I. Unit of stress is N m^-2 or Pa (pascal) and its dimensions are [L^-1M¹T^-2]. Units and dimensions of stress are the same as that of pressure.

The internal restoring force per unit area developed in a body when the body is compressed uniformly from all sides is called hydrostatic stress or hydraulic stress.

Volumetric strain:

When the deforming forces are such that there is a change in the volume of the body, then the strain produced in the body is called volume strain.

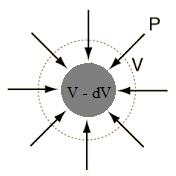
Mathematically

Volumetric strain = – Change in volume (dV)/ Original Volume (V)

The negative sign indicates the decrease in the volume

The volumetric strain has no unit and no dimensions.

Bulk Modulus of Elasticity:

Within the elastic limit, the ratio of volumetric stress to the corresponding volumetric strain in a body is always constant, which is called as Bulk modulus of elasticity.

It is denoted by the letter ‘K’. Its S.I. Unit of stress is N m^-2 or Pa (pascal) and its dimensions are [L^-1M¹T^-2].

Mathematically,

Characteristics of Bulk Modulus of Elasticity:

• Within the elastic limit, it is the ratio of volumetric stress to volumetric strain.
• It is associated with the change in the volume of a body.
• It exists in solids, liquids, and gases.
• It determines how much the body will compress under a given amount of external pressure.
• The bulk modulus of a material of a body is given by

Compressibility:

The reciprocal of bulk modulus of elasticity is called as compressibility. Mathematically

Compressibility = 1 / K

Its S.I. unit is m² N^-1 or Pa-1 and its dimensions are [L^-1M-¹T²].

Numerical Problems:

Example – 1:

A solid rubber ball has its volume reduced by 14.5% when subjected to uniform stress of 1.45 × 10⁴ N/m². Find the bulk modulus for rubber.

Given: Volumetric strain = 14.5 % = 14.5 × 10^-2, Volumetric stress =  1.45 × 10⁴ N/m²,

To Find: Bulk modulus of elasticity =?

Solution:

Bulk modulus of elasticity = K = Volumetric stress / Volumetric strain

∴  K = (1.45 × 10⁴) / (14.5 × 10^-2) = 10⁵ N/m²

Ans: Bulk modulus of elasticity of rubber is 10⁵ N/m²

Example -2:

What pressure should be applied to a lead block to reduce its volume by 10% Bulk modulus for lead = 6 × 10⁹ N/m²?

Given: Volumetric strain = 10 % = 10 × 10^-2 , Bulk modulus of elasticity =  6 × 10⁹ N/m².

To Find: Pressure intensity =?

Solution:

Bulk modulus of elasticity = K = Volumetric stress / Volumetric strain

∴ Volumetric stress = K ×Volumetric strain

∴ Pressure intensity = K ×Volumetric strain

∴ Pressure intensity = 6 × 10⁹ ×10 × 10^-2

∴ Pressure intensity = 6 × 10⁸ N/m²

Ans: Pressure intensity is 6 × 10⁸ N/m²

Example – 3:

A volume of 5 litres of water is compressed by a pressure of 20 atmospheres. If the bulk modulus of water is 20 × 10⁸ N/m². , find the change produced in the volume of water. Density of Mercury = 13,600 kg/m³; g = 9.8 m/s². Normal atmospheric pressure  = 75 cm of mercury.

Given: Original Volume = 5 L = 5 × 10^-3 m³, Pressure = dP = 20 atm = 20 × 75 × 10^-2 × 13600 × 9.8 N/m², Bulk modulus of elasticity of water =  20 × 10⁸ N/m².

To Find: Change in volume = dV =?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = (dP × V)/ dV

∴ Change in volume = dV = (dP × V)/ K

∴    dV =  5 × 10^-6  m³ = 5 cc

Ans: The change produced in the volume is 5 cc.

Example – 4:

A volume of 10^-3 m³ of water is subjected to a pressure of 10 atmospheres. The change in volume is 10^-6 m³. Find the bulk modulus of water. Atm. pressure = 10⁵ N/m².

Given: Original Volume = 10^-3 m³, Pressure = dP = 10 atm = 10 × 76 × 10^-2 × 13600 × 9.8 N/m², Change in volume = dV =10^-6 m³,

To Find: Bulk modulus of elasticity of water =?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = (dP × V)/ dV

∴ K = (10 × 76 × 10^-2 × 13600 × 9.8 × 10^-3)/ 10^-6

∴ K = 1.01 × 10⁹ N/m²

Ans: Bulk modulus of elasticity of water is 1.01 × 10⁹ N/m²

Example – 5:

Two litres of water, when subjected to a pressure of 10 atmospheres, are compressed by 1.013 cc. Find the compressibility of water.

Given: Original Volume = 2 L = 2 × 10^-3 m³, Pressure = dP = 10 atm = 10 × 76 × 10^-2 × 13600 × 9.8 N/m², Change in volume = dV =1.013 cc = 1.013 × 10^-6 m³,

To Find: Compressibility of water =?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = (dP × V)/ dV

∴  K = (10 × 76 × 10^-2 × 13600 × 9.8 × 2 × 10^-3)/(1.013 × 10^-6)

∴ K = 2 × 10⁹ N/m²

Compressibility = 1/K = 1/ (2 × 10⁹)

Compressibility = 5 × 10^-10 m²/N

Ans: Compressibility of water is 5 × 10^-10 m²/N

Example – 6:

Bulk modulus of water is 2.05 × 10⁹ N/m². What change of pressure will compress a given quantity of water by 0.5%?

Given: Bulk modulus of water = K = 2.05 × 10⁹ N/m², Volumetric strain = 0.5 % = 0.5 × 10^-2  = 5 × 10^-3 

To Find: Change in pressure = dP =?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = dP / Volumetric strain

∴ dP = K  × Volumetric strain

∴ dP = 2.05 × 10⁹  × 5 × 10^-3 

∴ dP = 1.025 × 10⁷  N/m²

Ans: Change in pressure is 1.025 × 10⁷  N/m²

Example – 7:

Calculate the change in volume of a lead block of volume 1 m³ subjected to pressure of 10 atmospheres. Also calculate compressibility of lead. 1 atm = 1.013 × 10⁵ N/m², K = 8 × 10⁵ N/m².

Given: Original Volume = 1 m³, Pressure = dP = 10 atm = 10 × 1.013 × 10⁵ N/m², Bulk modulus of elasticity = K = 8 × 10⁹ N/m².

To Find: Change in volume = dV =? Compressibility = ?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = (dP × V)/ dV

∴ Change in volume = dV =  (dP × V)/ K

∴ Change in volume = dV =  (10 × 1.013 × 10⁵ × 1)/ 8 × 10⁹

∴    dV =  1.27  × 10^-4 m³

Compressibility = 1/K = 1/ (8 × 10⁹)

Compressibility = 1.25 × 10^-10 m²/N

Ans: Change in volume is 1.27 × 10^-4 m³ and

compressibility of lead is 1.25 × 10^-10 m²/N

Example – 8:

Find the increase in the pressure required to decrease volume of mercury by 0.001%. Bulk modulus of mercury = 2.8 × 10¹⁰ N/m².

Given: Volumetric strain = 0.001% = 0.001 × 10^-2 = 10^-5, Bulk modulus of elasticity = 2.8 × 10¹⁰ N/m².

To Find: Pressure intensity =?

Solution:

Bulk modulus of elasticity = K = Volumetric stress / Volumetric strain

∴ Volumetric stress = K ×Volumetric strain

∴ Pressure intensity = K ×Volumetric strain

∴ Pressure intensity = 2.8 × 10¹⁰ × 10^-5

∴ Pressure intensity = 2.8 × 10⁵ N/m²

Ans: Pressure intensity is 2.8 × 10⁵ N/m²

Example – 9:

A solid brass sphere of volume 0.305 m³ is dropped in an ocean, where water pressure is 2 × 10⁷ N/m². The bulk modulus of water is 6.1 × 10¹⁰ N/m². What is the change in volume of the sphere?

Given: Original Volume = 0.305 m³, Pressure = dP = 2 × 10⁷ N/m²², Bulk modulus of elasticity = K =6.1 × 10¹⁰ N/m²

To Find: Change in volume = dV =?

Solution:

Volumetric Stress = Pressure intensity = dP

Bulk modulus of elasticity = K = (dP × V)/ dV

∴ Change in volume = dV = (dP × V)/ K

∴ Change in volume = dV = (2 × 10⁷ × 0.305)/ (6.1 × 10¹⁰)

∴    dV =  10^-4 m³

Ans: Change in volume = 10^-4 m³

Previous Topic: Behaviour of Ductile Material Under Increasing Load

Next Topic: Shear Stress, Shear Strain, and Modulus of Rigidity

Science > Physics > Elasticity > Volumetric Stress, Bulk Modulus of Elasticity