Science > Physics > Rotational Motion > Numerical Problems on Kinetic Energy and Angular Momentum
In this article, we shall study problems based on the change in kinetic energy and the change in angular momentum of a rotating body.
Example – 01:
A disc begins to rotate from rest with a constant angular acceleration of 0.5 rad/s2 and acquires an angular momentum of 73.5 kg m2/s in 15 s after the start. Find the kinetic energy of the disc in 20 s after the start.
Given: Angular acceleration = α = 0.5 rad/s2, Change in angular momentum = dL = 73.5 kg m2/s, time taken = t = 15 s, initial angular speed = ω1 = 0 rad/s
To find: K.E. in 20 s after start.
Solution:
We have, ω2 = ω1 + αt = 0 + 0.5 x 20 = 10 rad/s
Change in angular momentum = dL = L2 – L1 = Iω2 – Iω1
73.5 = I x 7.5 – I x 0
I = 73.5/7.5 = 9.8 kg m2
Now, Kinetic energy is given by
K.E. = ½ I ω2 = ½ x 9.8 x 102 = 490 J
Ans: The kinetic energy of the disc in 20 s after the start is 490 J
Example – 02:
The angular momentum of a body changes by 80 kg m2/s when its angular velocity changes from 20 rad/s to 40 rad/s. Find the changes in its K.E. of rotation.
Given: Change in angular momentum = 80 kg m2/s. Initial angular speed = ω1 = 20 rad/s, final angular speed = ω2 = 40 rad/s.
To Find: Change in kinetic energy =?
Solution:
Change in angular momentum = dL = L2 – L1 = Iω2 – Iω1
80 = I x 40 – I x 20
∴ 80 = 20 I
∴ I = 80/20 = 4 kg m2
Change in kinetic energy = K.E.2 – K.E.1 = ½ I ω22 – ½ I ω12 = ½ I ( ω22 – ω12)
Change in kinetic energy = ½ x 4 x (402 – 202)
Change in kinetic energy = 2 x (1600- 400) = 2400 J
Ans: The change in kinetic energy of rotation is 2400 J
Example – 03:
An energy of 500 J is spent to increase the speed of wheel from 60 r.p.m. to 240 r.pm. Calculate the moment of inertia of the wheel.
Given: Change in kinetic energy = 500 J, Initial angular speed = N1 = 60 r.pm., final angular speed = N2 = 240 r.p.m.
To Find: Moment of Inertia of the wheel.
Solution:
ω1 = 2πN1/60 = 2π x 60/60 = 2π rad/s
ω2 = 2πN2/60 = 2π x 240/60 = 8π rad/s
Change in K.E. = K.E.2 – K.E.1
∴ Change in K.E. = ½ Iω22 – ½ Iω12 = ½ I (ω22 – ω12)
∴ 500. = ½ I ((8π)2 – (2π)2)
∴ 1000. = I (64π2 – 4π2)
∴ 1000. = I (60π2)
∴ I = 1000/60π2 = 1.688 kgm2
Ans: The moment inertia of wheel is 1.688 kg m2
Example – 04:
A wheel of the moment of inertia 1 kgm2 is rotating at a speed of 30 rad/s. Due to friction on the axis, it comes to rest in 10 minutes. Calculate i) total work done by friction, ii) the average torque of the friction iii) angular momentum of the wheel two minutes before it stops rotating.
Given: Moment of inertia of wheel = 1 kg m2, Initial angular speed = ω1 = 30 rad/s, final angular speed = ω2 = 0 rad/s, time = t = 10 min = 10 x 60 = 600 s
To Find: Work done by friction =? Torque acting = ?, angular momentum of the wheel two minutes before it stops rotating.
Solution:
Work done by friction = Change in K.E. = K.E.1 – K.E.2
∴ Work done by friction. = ½ Iω12 – ½ Iω22 = ½ I (ω12 – ω22)
∴ Work done by friction. = ½ x 1 ((30)2 – (0)2) = 0.5 x 900 = 450 J
Now angular acceleration = α = (ω2 – ω1)/t = (0 – 30)/(10 x 60) = -30/600 = – 0.05 rad/s2
Negative sign indicates it is retardation.
The magnitude of angular acceleration = α = 0.05 rad/s2
Average torque = I α = 1 x 0.05 Nm. It is retarding torque
To find the angular momentum of the wheel two minutes before it stops rotating.
t = 10 min – 2 min = 8 min = 8 x 60 = 480 s.
ω2 = ω1+ αt = 30 – 0.05 x 480 = 30 – 24 = 6 rad/s
Angular momentum = Iω2 = 1 x 6 = 6 kg m/s2
Ans: Work done by friction is 450 J, Retarding torque acting is 0.05 Nm, angular momentum of the wheel two minutes before it stops rotating is 6 kg m/s2.
Example – 05:
A ceiling fan of a moment of inertia 30 kgm2 rotates about its own axis at the speed of 120 r.p.m. under the action of an electric motor of power 62.8 watts. If electric power is cut off, how many revolutions will it complete before coming to rest?
Given: Moment of inertia of fan = 30 kg m2, Initial angular speed = N1 = 120 r.p.m., final angular speed = ω2 = 0 rad/s,
To Find: Number of revolutions before coming to rest.
Solution:
ω1 = 2πN1/60 = 2π x 120/60 = 4π rad/s
Power = τ ω1 = I α ω1
∴ 62.8 = 30 x α x 4π
∴ 62.8 = 120π x α
∴ α = 62.8/(120 x 3.14) = 1/6 rad/s2.
ω22 = ω12 + 2α θ
∴ (0)2 = (4π)2 + 2(- 1/6) θ
∴ 0 = 16π2 – (1/3) θ
∴ (1/3) θ = 16π2
∴ θ = 48π2
No. of rotations = θ/2π = 48π2/2π = 24π = 24 x 3.14 = 75.36
Ans: Number of revolutions before coming to rest are 24π or 75.35
Example – 06:
When an angular velocity of a body changes from 20 rad/s to 40 rad/s, its angular momentum changes by 80 kgm2/s. Find the change in kinetic energy of rotation.
Given: Initial angular speed = ω1 = 20 rad/s, final angular speed = ω2 = 40 rad/s, Change in angular momentum = dL = 80 kgm2/s.
To Find: Change in kinetic energy of rotation =?
Solution:
Change in angular momentum = L2 – L1
∴ dL = Iω2 – Iω1 = I(ω2 – ω2)
∴ 80 = I(40 – 20) = 20 I
∴ I = 80/20 = 4 kg m2
Change in K.E. = K.E.2 – K.E.1
∴ Change in K.E. = ½ Iω22 – ½ Iω12 = ½ I (ω22 – ω12)
∴ Change in K.E. = ½ x 4 ((40)2 – (20)2) = 2 x (1600 – 400) = 2 x 1200 = 2400 J
Ans: the change in kinetic energy of rotation is 2400 J
Example – 07:
A flywheel of mass 2 kg has the radius of gyration of 0.2 m. Calculate the K.E. of rotation when it makes 5 revolutions per second.
Given: Mass of disc = M = 2 kg; radius of gyration = K = 0.2 m, Angular speed = n = 5 r.p.s.
To Find: Kinetic energy =?
Solution:
I = MK2 = 2 x (0.2)2 = 2 x 0.04 = 0.08 kg m/s
Now, K.E. = ½ Iω2 = ½ I (2πn)2 = ½ x 0.08 x ( 2 x 3.142 x 5)2
∴ K.E. = ½ Iω2 = ½ I(2πn)2 = 0.04 x ( 231..42)2 = 39.49 J
Ans: Kinetic energy of disc is 39.49 J
Example – 08:
A circular disc of mass 10 kg and radius 0.2 m is set into rotation about an axis passing through its centre and perpendicular to its plane by applying torque 10 Nm. calculate the angular velocity of the disc at the end of 6 s from rest.
Given: Mass of disc = M = 10 kg; radius of disc = R = 0.2 m, Torque acting = τ = 10 Nm, initial angular velocity = ω1 = 0 rad/s, time = t = 6 s
To Find: final angular velocity = ω2 =?
Solution:
Moment of Inertia of a disk is given by
I = ½ MR2 = ½ (10)(0.2)2 = 5 x 0.04 = 0.2 kg m2
Now, the torque acting on rotating body is given by
τ = I α
∴ 10 = 0.2 x α
∴ α = 10/0.2 = 50 rad/s2
Now, ω2 = ω1+ αt = 0 + 50 x 6 = 0 + 300 = 300 rad/s
Ans: The angular velocity of the disc at the end of 6 s from rest is 300 rad/s
Example – 09:
A torque of 400 Nm acting on a body of mass 40 kg produces an angular acceleration of 20 rad/s2. Calculate the moment of inertia and radius of gyration of the body.
Given: Mass of body = M = 40 kg; Torque acting = τ = 400 Nm, Angular acceleration = α = 20 rad/s2
To Find: Moment of inertia = I =? and radius of gyration = K = ?
Solution:
The torque acting on a rotating body is given by
τ = I α
∴ 400 = I x 20
∴ I = 400/20 = 20 kg m2
Now, I = MK2
∴ K2 = I/M = 20/40 = 0.5
∴ K = 0.707 m
Ans: Moment of inertia of the body is 20 kg m2 and the radius of gyration is 0.707 m.
Example – 10:
If the radius of a solid sphere is doubled by keeping its mass constant, compare the moment of inertia about any diameter.
Given: For sphere R2 = 2R1.
To Find: Ratio of the moment of inertia = I1/I2 =?
Solution:
The M.I. of a sphere in two cases about its diameter is given by

Ans: The ratio of the moment of inertia in two cases is 1:4
Example – 11:
A flywheel in the form of a disc is rotating about an axis passing through its centre and perpendicular to its plane loses 100 J of energy, when slowing down from 60 r.p.m. to 30 r.p.m. Find the moment of inertia about the same axis and change in its angular momentum.
Given: lost in energy = 100 J. Initial angular speed = N1 = 60 r.p.m., final angular speed = N2 = 30 r.p.m.,
To Find: Moment of inertia = I =? and change in angular momentum = dL =?
Solution:
ω1 = 2πN1/60 = 2π x 60/60 = 2π rad/s
ω2 = 2πN2/60 = 2π x 30/60 = π rad/s
Loss in K.E. = K.E.1 – K.E.2
∴ Loss in K.E. = ½ Iω12 – ½ Iω22 = ½ I (ω12 – ω22)
∴ 100 = ½ I ((2π)2 – (π)2)
∴ 200 = I (4π2 – π2)
∴ 200 = I (3π2)
∴ I = 200/3π2 = 6.753 kgm2
Change in angular momentum = L2 – L1
∴ dL = Iω1 – Iω2 = I(ω1 – ω2)
∴ dL = 6.753(2π – π) = 6.753 π = 6.753 x 3.142 = 21.22 kg m2/s
Ans: Moment of inertia is 6.753 kg m2 and change in angular momentum is 21.2 kg m2/s
Example – 12:
A disc of diameter 50 cm and mass 2 kg rotates about an axis passing through its centre and at right angles to its plane with a frequency of 8 revolutions per sec. Find the angular momentum of the disc and the rotational K.E.
Given: Diameter of disc = D = 50 cm, Radius of disc = 50/2 = 25 cm = 0.25 m, Mass of disk = M = 2 kg, Number of revolutions per second = n = 8
To Find: Angular momentum = L =? rotational kinetic energy = ?
Solution:
ω= 2πn = 2π x 8 = 16π rad/s
Moment of Inertia of a disk is given by
I = ½ MR2 = ½ (2)(0.25)2 = 1 x 0.0625 = 0.0625 kg m2
L = I ω = 0.0625 x 16π = 0.0625 x 16 x 3.142 = 3.142 kg m2/s
K.E. = ½ Iω2 = ½ x 0.0625 x (16π)2 = ½ x 0.0625 x 256 x 3.1422
K.E. = 78.98 J
Ans: Angular momentum is 3.142 kg m2/s and rotational K.E. is 78.98 J.
Example – 13:
A solid sphere of diameter 25 cm and mass 25 kg rotates about an axis through its centre. Calculate its moment of inertia if its angular velocity changes from 2 rad/s to 12 rad/s in 5 seconds. Also, calculate the torque applied.
Given: Diameter of sphere = D = 25 cm, Radius of sphere = 25/2 = 12.5 cm = 0.125 m, Mass of sphere = M = 25 kg, Initial angular speed = ω1 = 2 rad/s, final angular speed = ω2 = 12 rad/s,time = t = 5 s
To Find: Moment of inertia = I =? Torque required = τ = ?
Solution:
Moment of inertia of the sphere is given by
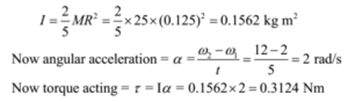
Ans: Moment of inertia is 0.1562 kg m2and torque acting is 0.3124 Nm
Example – 14:
Assuming that the earth is a uniform homogeneous sphere of radius 6400 km and density 5500 kg/m3, calculate its M. I. about its axis of rotation. What is the rotational K. E. of the earth when spinning about its axis?
Given: Radius of earth = 6400 km = 6.4 x 106 m, Density = 5500 kg/m3.
To Find: M.I. of earth =? K.E. of the earth =?
Solution:

Ans: Moment of inertia is 9.896 x 1037 kgm2 and kinetic energy is 2.612 x 1029 J
Example – 15:
Assuming the earth to be a sphere, calculate its M. I. about the axis of rotation. Calculate the angular momentum and rotational K. E. of the earth about its axis. Mass of earth = 6 x 1024kg; R = 6400 km.
Given: Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, Time period for earth = 24 hr = 24 x 60 x 60 s.
To Find: Moment of inertia = I =? Angular momentum = L = ?, Kinetic energy = ?
Solution:

Ans : Moment of inertia is 9.3 x 1037 kgm2 , angular momentum = 7.149 x 1033 kg m2/s, and kinetic energy is 2.612 x 1029 J
Example – 16:
Find the ratio of the spin angular momentum of the earth to its orbital angular momentum. Distance of earth from the sun = 1.5 x 108 km; Radius of earth = 6400 km; Mass of earth = 6 x 1024 kg. One year = 365 days.
Given: Distance of earth from the sun = r = 1.5 x 108 km; Radius of earth = R =6400 km = 6.4 x 106 m; Mass of earth = 6 x 1024 kg, Time period for orbital motion = To = 365 days = 365 x 24 x 60 x 60 s, spin period = 24 hr = 24 x 60 x 60 s.
To Find: Ratio of the spin angular momentum of the earth to its orbital angular momentum
Solution:

Ans: The ratio of the spin angular momentum of the earth to its orbital angular momentum is 2.658 x 10-7.
Previous Topic: The Concept of Angular Momentum
For More Topics in Physics Click Here