Science > Physics > Themodynamics > Correction to the Ideal Gas Equation
In this article, we shall study the correction to ideal gas equation.
Ideal Gas Equation:
The equation of state for an ideal gas is given by
PV = n RT
Where, P = Pressure of gas, V = Volume of gas, n = No. of moles of gas
R = Universal gas constant, T = Absolute temperature of gas.
For one mole of gas, PV = RT
Van Der Wall’s Correction to Ideal Gas Equation:
Necessity of Correction of Ideal Gas Equation:
While deriving the ideal gas equation PV = RT, we had assumed that
- The volume occupied by the gas molecules themselves is negligible compared with the total volume of the gas, and
- The molecules exert no appreciable force on one another.
Both of these assumptions cannot be true at high pressure. When the gas is at high pressure, it has a small volume and therefore volume actually occupied by an individual molecule of a gas cannot be neglected in comparison with the volume of the entire gas.
Also, at high pressure, the molecules come closer, therefore considerable cohesive forces ‘will be acting on them. Thus at high pressure and low temperature, the real gases do not obey the above relation.
While modifying the perfect gas equation, PV = RT, both these factors were considered by van der Waals.
Correction for Volume:
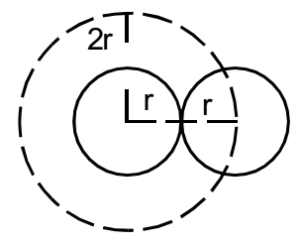
Let us consider a container containing the gas. The gas molecules are like hard elastic spheres. Let us assume that ‘r’ is their radius. Thus the distance between two molecules cannot be less than ‘2r’. Thus the presence of one molecule in the container will reduce the space available for another molecule by amount
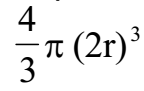
Thus the space available for free motion of gas molecules is less than the actual volume of the gas. Therefore, the corrected volume is taken as (V – b).
The correction term ‘b’ is called co-volume and is equal to four times the actual volume occupied by the molecules.

Where N0 is no. of molecules of gas in the container
Correction for Intermolecular Attraction:

Consider a molecule A in the interior, far from the boundary. It is surrounded by other molecules equally distributed in all directions. Due to the similar forces (cohesive forces) acting upon it, symmetrically, from all sides the net intermolecular force acting on it is zero.
Now, let us consider another gas molecule B near a wall of the container as shown in the figure. The cohesive force on B is due to adjacent molecules and the adhesive force due to the attraction between atoms of the wall with which molecule collides. Due to this inward pull acts on molecule B. Thus there is a small inward pressure p in addition to observed pressure P. Therefore corrected pressure is (P + p). The inward pressure depends upon
- The number of molecules striking per unit area of the wall per unit time (p ∝ n) and
- The number of attracting molecules per unit volume which attract the colliding molecule. (p ∝ n). Both these factors are proportional to the density of the gas.
Thus, p ∝ n²
If N be the number of molecules present in volume V of the gas, then n = N / V

where ‘a’ is some constant and V is the volume of the gas. Therefore, corrected pressure ( P + p) becomes

Thus van der walls corrected equation for one mole of gas is

Drawbacks of Van der wall’s Correction:
- According to Van der walls, a and b are constants for given gas, but it is found that the constants a and b change in temperature.
- The shape of theoretical isotherm plotted using Van der walls equation is different from the experimentally drawn isotherm.