Science > Physics > Units and Measurements > More Problems on Dimensional Analysis
Example – 01:
Check the correctness of physical equation, s = ut +1/2at2, Where u is the initial velocity, v is the final velocity, a is the acceleration, s is the displacement and t is the time in which the change occurs.
Solution:
Given equation is s = ut +1/2at2
L.H.S. = v, hence [L.H.S.] = [s] = [L1M0T0] ………………. (1)
R.H.S = ut +1/2at2 , hence [R.H.S] = [u][t]+ [t]2
= [L1M0T-1][L0M0T1] + [L1M0T-2][L0M0T1]2
[R.H.S] = [L1M0T0] + [L1M0T-2][L0M0T2]
[R.H.S] = [L1M0T0] + [L1M0T0]
[R.H.S] = [L1M0T0] ……………. (2)
From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally correct.
Example – 02:
Check the correctness of physical equation, F = mv²/r, Where F is the centripetal force acting on a body of mass m performing uniform circular motion along a circle of radius r with linear speed v.
Solution:
Given equation is F = mv²/r
L.H.S. = F, hence [L.H.S.] = [F] = [L1M1T-2] ………………. (1)
R.H.S = mv²/r , hence [R.H.S] = [m][v]²/[r]
[R.H.S] = [L0M1T0][L1M0T-1]2 / [L1M0T0]
[R.H.S] = [L0M1T0][L2M0T-2] [L-1M0T0]
[R.H.S] = [L1M1T-2] ……………. (2)
From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally correct.
Example – 03:
Check the correctness of physical equation, v2 = u2 + 2as2
Solution:
Given equation is v2 = u2 + 2as2
L.H.S. = v2, hence [L.H.S.] = [v]2 = [L1M0T-1]2 = [L2M0T-2] ………………. (1)
R.H.S = u2 + 2as2
hence [R.H.S] = [u]2 + 2[a][s]2
[R.H.S] = [L1M0T-1]2 + [L1M0T-2][L1M0T0]2
[R.H.S] = [L2M0T-2] + [L1M0T-2][L2M0T0]
[R.H.S] = [L2M0T-2] + [L3M0T-2] ……………. (2)
From (1) and (2) we have [L.H.S.] ≠ [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally not correct.
Example – 04:
Check the correctness of physical equation, when the frequency of vibration ‘n’ of a string of length ‘l’ having mass per unit length ‘m’ kept under tension ‘F’ is given by
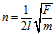
Solution:
Given equation is
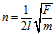
L.H.S. = n, hence [L.H.S.] = [n] = [L0M0T-1] ………………. (1)
R.H.S = (1/2l) (F/m)1/2 , hence [R.H.S] = [1/l](F/m)1/2
[R.H.S] = [l]-1[F]1/2[M]-1/2
[R.H.S] = [L1M0T0]-1[L1M1T-2]1/2 [L-1M1T0]-1/2
[R.H.S] = [L-1M0T0][L1/2M1/2T-1] [L1/2M-1/2T0]
[R.H.S] = [L-1+1/2+1/2M1/2-1/2T-1]
[R.H.S] = [L0M0T-1] ……………. (2)
From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally correct.
Example – 05:
Check the homogeneity (correctness of physical equation) of the equation, when the rate of flow of a liquid having a coefficient of viscosity’η’ through a capillary tube of length ‘l’ and radius ‘a’ under pressure head ‘p’ is given by

Solution:
Given equation is


From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally homogeneous.
Example – 06:
Check the homogeneity (correctness of physical equation)of the equation, when the periodic time ‘T’ of vibration of the magnet of the moment of inertia ‘I’, magnetic moment, ‘M’ vibrating in magnetic induction ‘B’ is given by

Solution:
Given equation is


From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally homogeneous.
Example – 07:
Check the homogeneity of the equation, when the terminal velocity ‘v’ of a small sphere of radius ‘a’ and density ‘ρ’ falling through a liquid of density ‘σ’ and coefficient of viscosity ‘η’ is given by

Solution:
Given equation is


From (1) and (2) we have [L.H.S.] = [R.H.S.]
Hence by the principle of homogeneity, the given equation is dimensionally homogeneous.
Example – 08:
A force F is given by F = at + bt2, where t is the time. Find the dimensional formula of ‘a’ and ‘b’.
Solution:
By the principle of homogeneity the dimensions on either side of the physical equation must be the same. Now two physical quantities can be added or subtracted if and only if their dimensions are the same.
Dimensions of F = Dimensions of at
[L1M1T-2] = [a] [t]
[a] =[L1M1T-2] / [T]
[a]=[L1M1T-3]
Similarly, dimensions of F = Dimensions of bt2
[L1M1T-2] = [b] [T] 2
[b]= [L1M1T-2] / [T2]
[b]= [L1M1T-4]
Ans: The dimensional formula of ‘a’ and ‘b’ are [M1L1T-3 ] and [M1L1T-4].
Example – 09:
The distance covered by a body in time t is given by the relation S = a + bt + ct2. What are the dimension of a,b,c ? Also write the quantities they represent.
Solution:
By the principle of homogeneity the dimensions on either side of the physical equation must be the same. Now two physical quantities can be added or subtracted if and only if their dimensions are the same.
Dimensions of S = Dimensions of a
[L1M0T0] = [a]
Dimensions of ‘a’ are that of displacement. Hence ‘a’ represent the displacement.
Dimensions of S = Dimensions of bt
[L1M0T0] = [b] [t]
[b] =[L1M0T0] / [T]
[b]=[L1M0T-1]
Dimensions of ‘b’ are that of velocity. Hence ‘b’ represent the velocity.
Dimensions of S = Dimensions of ct2
[L1M0T0] = [c] [T] 2
[c]= [L1M0T0] / [T2]
[b]= [L1M0T-2]
Dimensions of ‘c’ are that of acceleration. Hence ‘c’ represent the acceleration.
Ans: The dimensional formula of ‘a’, ‘b’ and ‘c’ are [L1M0T0], [L1M0T-1], and [L1M0T-2] and the quantities represented by a, b and c are displacement, velocity and acceleration.
Example – 10:
According to Laplace’s formula, the velocity ( V) of sound in a gas is given by v = (γP / d)1/2, where P is the pressure, d is the density of a gas. What is the dimensional formula for γ?
Solution:

Ans: The dimensional formula for γ is [ M0 L0 T0 ]
Example – 11:
In an equation { P + a / V2 } (V – b) = RT, where P is the pressure, V is the volume, T is the temperature and a, b, R are constants. What is the dimensional formula of a /b?
Solution:
Two physical quantities can be added or subtracted if and only if their dimensions are the same.
Thus the dimensions of P and a / V2 are same

Dimensions of b = Dimensions of V
[b] = [L3M0T0]
Now [a]/[b] = [L5M1T-2]/ [L3M0T0] = [L2M1T-2]
Ans: The dimensional formula of a /b is [ M1 L2 T-2 ]
Example – 12:
A force is given in terms of distance x and time t by F = A sin Ct + B cos Dx. Then what are the dimensions of A/B and C/D?
Solution:
By the principle of homogeneity the dimensions on either side of a physical equation must be the same. The trigonometric ratios sin and cos are pure ratios of length, hence are dimensionless quantity.
Thus [A] = [B] =[F] = [ M1 L1 T-2 ]
Thus dimensions of A/B are [ M0 L0 T0 ]
Now the angle is dimensionless quantity
[C][t] = [ M0 L0 T0 ]
[C] = [ M0 L0 T0 ]/ [T] = [ M0 L0 T-1 ]
[D][x] = [ M0 L0 T0 ]
[D] = [ M0 L0 T0 ]/ [L] = [ M0 L-1 T0 ]
[C]/[D] = [ M0 L0 T-1 ]/ [ M0 L-1 T0 ] = [ M0 L1 T-1 ]
Ans: The dimensions of A/B and C/D are [M0L0T0] [M0L1 T-1]
Example – 13:
In a equation { P + a / V2 } ( V – b) = constant , where P is the pressure, V is the volume and a, b are constants. Find the unit of ‘a’.
Solution:
Two physical quantities can be added or subtracted if and only if their units are the same.
Thus the units of P and a / V2 are same
Unit of P = Unit of a /(unit of V)2
dyne cm-2 = unit of a / (cm3) 2
dyne cm-2 = unit of a / cm6
unit of a = dyne cm-2 x cm6 = dyne cm4
Ans: The unit of a is dyne cm4
Example – 14:
What are the dimensions of constant C in the equation P + ½ρv2 + hρg = C? Where P is pressure, ρ is a density, v is the velocity of liquid flow, h is the height and g is the acceleration due to gravity.
Solution:
Two physical quantities can be added or subtracted if and only if their units are the same. Thus the dimension of P, ½ρv2, hρg, and C should be that of pressure.
Dimensions of C = Dimensions of P = [M1L-1 T-2]
Ans: The dimensions of C are[M1L-1 T-2]
Example – 15:
The velocity v, the acceleration a and displacement s of a body in motion are related by the expression v2 ∝ axsy. Find x and y.
Solution:
Given v2 ∝ axsy
∴ v2 = k axsy
∴ [M0L1 T-1]2 = [M0L1 T-2]x[M0L1 T0]y
∴ [M0L2 T-2]2 = [M0Lx T-2x] [M0Ly T0]
∴ [M0L2 T-2]2 = [M0Lx + y T-2x]
∴ x + y = 2 and -2x = -2 i.e. x = 1 and y = 1
Ans: x = 1 and y = 1
Previous Topic: Applications of Dimensional Analysis
Next Topic: Problems on Form of Physical Equation

3 replies on “More Problems on Dimensional Analysis”
The solution of example number 4 is incorrect. Please send the correct solution to that example.
Thank you for correction. Correction implimented
Thanks