Dimensions of Physical Quantities

Science > Physics > Units and Measurements > Dimensions of Physical Quantities

In this article, we shall study the concept of dimensions of physical quantities and to find dimensions of given physical quantity.

Dimensions of Physical Quantity:

The power to which fundamental units are raised in order to obtain the unit of a physical quantity is called the dimensions of that physical quantity. Dimensions of physical quantity do not depend on the system of units.

If ‘A’ is any physical quantity, then the dimensions of A are represented by [A]. Mass, length and time are represented by M, L, T respectively. Therefore, the dimensions of fundamental quantities are as follows:

• [Mass] = [M]
• [Length] = [L]
• [Time] = [T]

Now electric current (I) and temperature (K) are also considered as fundamental quantities and using them the dimensions of electrical quantities are found. An expression, which gives the relation between the derived units and fundamental units in terms of dimensions is called a dimensional equation. Thus the dimensional equation of speed is[L¹M⁰T^-1] and 1, 0, -1 are called dimensions.

Dimensions of Some Physical Quantities:

Sr.No.	Derived Quantity	Dimensions	S.I. Unit	Symbol
1	Area	[L2M0T0]	square metre	m2
2	Volume	[L3M0T0]	cubic metre	m3
3	Density	[L-3M1T0]	kilogram per cubic metre	Kg/m3
4	Velocity	[L1M0T-1]	metre per second	m/s
5	Acceleration	[L1M0T-2]	metre per square second	m/s2
6	Momentum	[L1M1T-1]	kilogram metre per second	Kg m/s
7	Force	[L1M1T-2]	newton	N
8	Impulse	[L1M1T-1]	newton second	Ns
9	Work	[L2M1T-2]	joule	J
10	Kinetic energy	[L2M1T-2]	joule	J
11	Potential energy	[L2M1T-2]	joule	J
12	Power	[L2M1T-3]	watt	W
13	Pressure	[L-1M1T-2]	newton per square metre	N/m2
14	Electric charge	[L0M0T1I1]	coulomb	C
15	Electric current	[L2M1T-3I-1]	ohm	Ω
16	Electric potential	[L2M1T-3I-2]	volt	V

Derivation of Dimensions of Some Physical Quantity:

We should know following facts before finding dimensions of other physical quantities.

The dimensions of length (l), breadth (b), height (h), depth (d), thickness (t), width (w), circumference (c), perimeter (p), distance (S), displacement (S), radius (r), diameter (D) are [L¹M⁰T⁰]

Dimensions of mass are [L⁰M¹T⁰] and that of time are [L⁰M⁰T¹].

Dimensions and Unit of Area (A):

Area = Length × Breadth

∴ A = l × b

∴ [A] = [l] × [b]

∴ [A] =[L¹M⁰T⁰][L¹M⁰T⁰]

∴  [A] =[L²M⁰T⁰]

Dimensions of area are [L²M⁰T⁰]

S.I. Unit of the area is square metre (m²). c.g.s. unit of area is square centimetre (cm²)

Dimensions and Unit of Volume (V):

Volume = Length × Breadth × Height

∴  V = l × b × h

∴  [V] = [l] × [b] × [h]

∴  [V] = [L¹M⁰T⁰][L¹M⁰T⁰][L¹M⁰T⁰]

∴  [V] = [L³M⁰T⁰]

Dimensions of volume are [L³M⁰T⁰]

S.I. Unit of volume is cubic metre (m³). c.g.s. unit of volume is cubic centimetre3 (cm³).

Dimensions and Unit of Density (ρ or d):

Dimensions of density are [L^-3M¹T⁰]

S.I. Unit of density is kilogram per cubic metre (kg m3 or kg m^-3). c.g.s. unit of density is gram per cubic centimetre (g cm^-3)

Dimensions and Unit of Velocity or Speed (v):

Dimensions of velocity or speed are [L¹M⁰T^-1]

S.I. Unit of velocity or speed is metre per second (m s^-1). c.g.s. unit of velocity or speed is centimetre per second (cm s^-1).

Dimensions and Unit of Acceleration (a or f):

Dimensions of acceleration are [L¹M⁰T^-2]

S.I. Unit of acceleration is metre per square second (m s^-2).

c.g.s. unit of acceleration is centimetre per square second (cm s^-2).

Dimensions and Unit of Force (F):

Force = Mass × Acceleration

∴  F = m× a

∴  [F] = [m] × [a]

∴  [F] = [L⁰M¹T⁰][L¹M⁰T^-2]

∴  [F] = [L¹M¹T^-2]

Dimensions of force are [L¹M¹T^-2]

S.I. Unit of force is kilogram metre per square second (kg m s^-2), This unit is known as newton (N).

c.g.s. unit of acceleration is gram centimetre per square second (g cm s^-2). This unit is known as dyne.

Dimensions and Unit of Momentum (p):

Momentum = Mass × Velocity

∴  p = m× v

∴  [p] = [m] × [v]

∴  [p] = [L⁰M¹T⁰][L¹M⁰T^-1]

∴  [p] = [L¹M¹T^-1]

Dimensions of momentum are [L¹M¹T^-1]

S.I. Unit of momentum is kilogram meter per second (kg m s^-1).

c.g.s. unit of momentum is gram centimeter per second (g cm s^-1)

Dimensions and Unit of Impulse of Force (J):

Impulse of Force = Force × Time

∴  J =F× t

∴  [J] = [F] × [t]

∴  [J] = [L¹M¹T^-2][L⁰M⁰T¹]

∴  [J] = [L¹M¹T^-1]

Dimensions of impulse of force are [L¹M¹T^-1]

S.I. Unit of impulse of force is kilogram meter per second (kg m s^-1). Common S.I. unit used is newton second (N s).. c.g.s. unit of impulse of force is gram centimeter per second (g cm s^-1). Common c.g.s. unit is dyne second.

Dimensions and Unit of Work (W):

Work Done = Force × Displacement

∴ W =F× s

∴  [W] = [F] × [s]

∴  [W] = [L¹M¹T^-2][L¹M⁰T⁰]

∴  [W] = [L²M¹T^-2]

Dimensions of work are [L²M¹T^-2]

S.I. Unit of work is kg square metre per square second. Commonly this unit is known as joule (J).

c.g.s. Unit of work is gram square centimetre per square second. Commonly this unit is known as erg.

Dimensions and Unit of Potential Energy (E or U):

Potential Energy = Mass × Acceleration due to gravity × Height

∴ E =m× g × h

∴  [E] = [m] × [g] × [h]

∴  [E] = [L⁰M¹T⁰][L¹M⁰T^-2][L¹M⁰T⁰]

∴  [E] = [L²M¹T^-2]

Dimensions of potential energy are [L²M¹T^-2]

S.I. Unit of potential energy is kg square metre per square second. Commonly this unit is known as joule (J).

c.g.s. Unit of potential energy is gram square centimetre per square second. Commonly this unit is known as erg.

Dimensions and Unit of Kinetic Energy (E):

Kinetic Energy = 1/2 Mass × Velocity²

∴ E =1/2×m ×v²

∴  [E] = [m] × [v]²

∴  [E] = [L⁰M¹T⁰][L¹M⁰T^-1]²

∴  [E] = [L⁰M¹T⁰][L²M⁰T^-2]

∴  [E] = [L²M¹T^-2]

Dimensions of kinetic energy are [L²M¹T^-2]

S.I. Unit of kinetic energy is kg square metre per square second. Commonly this unit is known as joule (J).

c.g.s. Unit of kinetic energy is gram square centimetre per square second. Commonly this unit is known as erg.

Dimensions and Unit of Pressure (P):

Dimensions of Pressure are [L^-1M¹T^-2] S.I. Unit of pressure is

S.I. Unit of pressure is newton per square metre or pascal (N m^-2 or Pa).

c.g.s. unit of pressure  is dyne per square centimetre (dyne cm^-2)

Dimensions and Unit of Power (P):

Dimensions of Power are [L²M¹T^-3]

S.I. Unit of Power is watt (W). c.g.s. unit of power  is erg per second (erg s^-1)

 Dimensions and Unit of Electric Charge:

Electric Charge = Electric Current × Time

∴ Q =I× t

∴  [Q] = [I] × [t]

∴  [Q] = [L⁰M⁰T⁰I¹][L⁰M⁰T¹]

∴  [Q] = [L⁰M⁰T¹I¹]

Dimensions of electric charge are [L⁰M⁰T¹I¹]

S.I. Unit of electric charge is coulomb (C)

Dimensions and Unit of Electric Potential:

Dimensions of electric potential are [L²M¹T^-3I^-1]

S.I. Unit of electric potential is volt (V)

Dimensions and Unit of Electric Resistance:

Dimensions of electric resistance are [L²M¹T^-3I^-2]

S.I. Unit of electric resistance is ohm (Ω)

Previous Topic: Measurement of Time

Next Topic: Applications of Dimensional Analysis

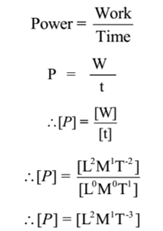
Science > Physics > Units and Measurements > Dimensions of Physical Quantities