Science > Physics > Surface Tension > Laplace’s Law of Spherical Membrane
In this article, we shall study Laplace’s Law about the excess of pressure inside a drop or a bubble of a liquid.
Excess of Pressure Inside a Drop of a Liquid and Soap Bubble:
Due to surface tension, free liquid drops and bubbles are spherical, if the effect of gravity and air resistance are negligible. Due to the spherical shape, the inside pressure Pi is always greater than the outside pressure Po. The excess of pressure is Pi– Po.
Laplace’s Law of a Spherical Membrane for a Liquid Drop:
Due to the spherical shape, the inside pressure Pi is always greater than the outside pressure Po. The excess of pressure is Pi– Po.
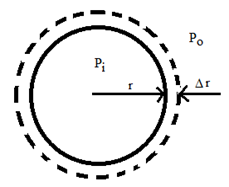
Let the radius of the drop increases from r to r + Δr, where Δr is very very small, hence the inside pressure is assumed to be constant.
Initial surface area = A1 = 4 π r²
Final surface area = A2 = 4 π (r + Δr)²
Final surface area = 4 π (r² + 2r.Δr + Δr²)
Final surface area = 4 πr² + 8 πr.Δr + 4 πΔr²
Δr is very very small, hence Δr² still smsll hence the term 4 πΔr² can be neglected.
Final surface area = A2 = 4 πr² + 8 πr.Δr
Hence Change in area = A2 – A1 = 4 πr² + 8 πr.Δr – 4 πr²
Change in area = dA = 8 πr.Δr
Now, work done in increasing the surface area is given by
dW = T. dA = T. 8 πr.Δr …………… (1)
By definition of work in mechanics we have
dW = Force ∴ displacement = F .Δr …………… (2)
But P = F /A, Hence F = Excess pressure × Area
F = (Pi– Po) × 4 πr²
Substituting in equation (2) we have
dW = (Pi– Po) × 4 πr².Δr …………… (3)
From equations (3) and (4) we have
(Pi– Po) × 4 πr².Δr = T. 8 πr.Δr
(Pi– Po) = 2T / r
This relation is known as Laplace’s law for the spherical membrane for a liquid drop.
Laplace’s Law of a Spherical Membrane for a Liquid Bubble:
Due to the spherical shape, the inside pressure Pi is always greater than the outside pressure Po. The excess of pressure is Pi– Po.

Let the radius of the bubble increases from r to r + Δr, where Δr is very very small, hence the inside pressure is assumed to be constant.
Bubble has two free surfaces, one inside and another outside
Initial surface area = A1 = 2 × 4 π r² = 8 π r²
Final surface area = A2 = 2 × 4 π (r + Δr)²
Final surface area = 8 π (r² + 2r.Δr + Δr²)
Final surface area = 8 πr² + 16 πr.Δr + 8 πΔr²
Δr is very very small, hence Δr² still smsll hence the term 8 πΔr² can be neglected.
Final surface area = A2 = 8 πr² + 16 πr.Δr
Hence Change in area = A2 – A1 = 8 πr² + 16 πr.Δr – 8 πr²
Change in area = dA = 16 πr.Δr
Now, work done in increasing the surface area is given by
dW = T. dA = T. 16 πr.Δr …………… (1)
By definition of work in mechanics we have
dW = Force × displacement = F .Δr …………… (2)
But P = F /A, Hence F = Excess pressure × Area
F = (Pi– Po) × 4 πr²
Substituting in equation (2) we have
dW = (Pi– Po) × 4 πr².Δr …………… (3)
From equations (3) and (4) we have
(Pi– Po) × 4 πr².Δr = T. 16 πr.Δr
(Pi– Po) = 4T / r
This relation is known as Laplace’s law for spherical membrane for a liquid bubble.
Difference in Pressure Across the Surface Film:
Rise and fall of liquid in a capillary tube can be explained by knowing the fact that a pressure difference exists across a curved free surface of the liquid.
When the liquid surface is flat:

In this case, the surface tension is horizontal and hence has no normal component to the horizontal surface. Due to which there is no extra pressure on outside or inside. Thus the pressure on the liquid side is equal to the pressure on the vapour side.
When the liquid surface is concave:

In this case, the component of surface tension acts vertically upward. Due to which pressure inside liquid decreases. Thus for the equilibrium of concave surface, the pressure on the vapour side should be more than that on the liquid side. Hence liquid rises in the capillary tube. In this case, the adhesion is greater than the cohesion.
When the liquid surface is convex:

In this case, the component of surface tension acts vertically downward. Due to which pressure inside liquid increases. Thus for the equilibrium of convex surface, the pressure on the vapour side should be less than that on the liquid side. Hence liquid dips in the capillary tube. In this case, the cohesion is greater than the adhesion.
Conclusion:
In case 2 and 3 we can see that, when liquid surface is curved, the surface tension give rises to a pressure which is directed towards the centre of curvature of the surface, to balance this there is excess pressure acting on the surface. Thus, there is always excess of pressure on the concave side of a curved liquid surface over the pressure on its convex side due to surface tension.
Numerical Problems on Excess of Pressure:
Example – 1:
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. Surface tension of water = 0.072 N/m. Atmospheric pressure = 1.013 x 105 N/m².
Given: Diameter of soap bubble = 4 mm, Radius of raindrop = r = 4/2 = 2 mm = 2 × 10-3 m, Surface tension = T = 0.072 N/m, Outside pressure = Po = Atmospheric pressure = 1.013 × 105 N/m².
To Find: Inside pressure = Pi =?
Solution:
By Laplace’s law of spherical membrane for a drop
(Pi– Po) = 2T / r
∴ Pi = (2T / r) + Po
∴ Pi = (2 × 0.072 / 2 × 10-3) + 1.013 × 105
∴ Pi =72 + 1.013 × 105
∴ Pi = 1.01372 × 105 N/m²
Ans: The pressure inside the raindrop is 1.01372 × 105 N/m²
Example – 2:
Find the excess pressure inside the soap bubble of diameter 3 cm. The surface tension of the soap solution is 3 × 10-2 N/m.
Given: Diameter of soap bubble = 3 cm, Radius of soap bubble = r = 3/2 =1.5 cm = 1.5 × 10-2 m, Surface tension = T = 3 × 10-2 N/m
To Find: excess pressure = (Pi– Po) =?
Solution:
By Laplace’s law of spherical membrane for a bubble
(Pi– Po) = 4T / r
∴ (Pi– Po) = 4 × 3 × 10-2 / 1.5 × 10-2
∴ (Pi– Po) = 8 N/m²
The excess pressure inside the soap bubble is 8N/m²
Example – 3:
What should be the diameter of a soap bubble, in order that the excess pressure inside it is 51.2 N/m². The surface tension of the soap solution is 3.2 × 10-2 N/m.
Given: excess pressure = (Pi– Po) = 51.2 N/m², Surface tension = T = 3.2 × 10-2 N/m
To Find: Diameter of soap bubble =?
Solution:
By Laplace’s law of spherical membrane for a bubble
(Pi– Po) = 4T / r
∴ r = 4T / (Pi – Po)
∴ r = 4 × 3.2 × 10-2 / 51.2
∴ r = 2.5 × 10-3 m = 2.5 mm
Diameter of soap bubble = 2 × 2.5 mm = 5 mm
Ans: The diameter of soap bubble is 5 mm
Previous Topic: Concept of Angle of Contact
Next Topic: The Concept of Capillary Action
3 replies on “Laplace’s Law of Spherical Membrane”
Really good.
I Am Galadima Usman .D. In Nassarawa State Nigeria Am Vary Appreciated That I Have Chose Physic,
This is a very educative content, it explained Laplace’s law of Spherical membrane in minutes.
God bless you for this.