Science > Physics > Elasticity > Longitudinal Stress and Strain
In this article, we shall study the concept of stress, strain, and modulus of elasticity. Main focus will be on longitudinal stress, longitudinal strain, and Young’s modulus of elasticity.
Concept of Stress:
The net internal elastic force (restoring force) acting per unit area of the surface which is subjected to deformation is called stress.
Stress = F / A
Stress is denoted by the letter ‘σ’. S.I. unit of stress is N m-2 (newton per square meter) or Pa (pascal) and its dimensions are [L-1M1T-2]. Units and dimensions of stress are the same as that of pressure.
Characteristics of Stress:
- Stress is an internal restoring force per unit area.
- It opposes the change in the size, shape or both of the body. i.e. it opposes deformation.
- It is a tensor quantity.
- Its S.I. unit is Nm-2 and its dimensions are [L-1M1T-2].
Concept of Strain:
The change in dimension per unit original dimension of a body subjected to deforming forces is called Strain.
Strain = Change in dimension / Original dimension
A strain is denoted by letter ‘e’. It is a pure ratio, (Ratio of two similar quantities) hence it is unitless, dimensionless quantity [L0M0T0].
Characteristics of Strain:
- The strain is defined as the ratio of change in dimensions of a body to its original dimensions when subjected to deformation.
- For longitudinal loading, both the longitudinal and lateral strain are produced.
- It is a scalar quantity.
- it is unit less, dimension less quantity.
Hooke’s Law of Elasticity:
Statement: Within the elastic limit, the stress developed in the body is directly proportional to the strain produced in the body.
By Hooke’s Law,
Stress ∝ Strain
∴ Stress = Constant x Strain
∴ Stress / Strain = Constant
This constant of proportionality is called the modulus of elasticity or coefficient of elasticity. Its units and dimensions are the same as that of stress. Its S.I. unit is N m-2 (newton per square meter) or Pa (pascal) and its dimensions are [L-1M1T-2]. Depending upon the nature of stress and strain these constants are further classified as (1) Young’s modulus of elasticity (2) Bulk modulus of elasticity and (3) Modulus of rigidity.
Graphical Representation:
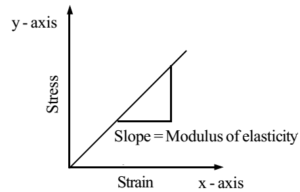
Characteristics of Modulus of Elasticity:
- The ratio of the stress produced in a body to corresponding stress produced in it is called the modulus of elasticity of the material of the body.
- It is the characteristic property of the material of the body.
- Its S.I. unit is Nm-2 and its dimensions are [L-1M1T-2].
- Depending upon loading there are three types of elasticity constant. If there is a change in the length of a body then the corresponding elastic constant is called Young’s modulus of elasticity. If there is a change in the volume of a body then the corresponding elastic constant is called the bulk modulus of elasticity. If there is a change in the shape of a body then the corresponding elastic constant is called modulus of rigidity.
Elastic Limit:
It is the upper limit of deforming force up to which if the deforming force is removed, the body regains its original shape and size completely. If the deforming force is increased beyond this limit, there is permanent deformation in the body called a permanent set. Elastic limit is a property of a body, while elasticity is the property of the material of the body.
Longitudinal Loading (Along the Length):
Longitudinal stress:
When the deforming forces are such that there is a change in the length of the body, then the stress produced in the body is called longitudinal stress. Longitudinal stress is further classified into two types. Tensile stress and compressive stress.
Longitudinal stress = F / A
Stress is denoted by the letter ‘σ’. S.I. unit of stress is N m-2 (newton per square meter) or Pa (pascal) and its dimensions are [L-1M1T-2]. Units and dimensions of stress are the same as that of pressure.
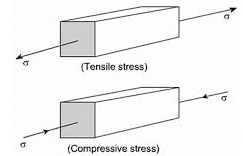
Tensile stress:
When the deforming force is such that there is the increase in the length of the body, then the stress produced in the body is called tensile stress.
Compressive stress:
When the deforming force is such that there is a decrease in the length of the body, then the stress produced in the body is called compressive stress.
Longitudinal strain:
When the deforming forces are such that there is a change in the length of the body, then the strain produced in the body is called longitudinal strain. The longitudinal strain is further classified into two types. Tensile strain and tensile strain. Mathematically the longitudinal strain is given by
Longitudinal strain = Change in length(l) / Original length (L)
The longitudinal strain has no unit and no dimensions.
Tensile strain:
When the deforming force is such that there is an increase in the length of the body, then the strain produced in the body is called tensile strain.
Compressive strain:
When the deforming force is such that there is a decrease in the length of the body, then the strain produced in the body is called compressive strain.
Click the Following Link for Video Lecture
Young’s Modulus of Elasticity:
Within the elastic limit, the ratio of the longitudinal stress to the corresponding longitudinal strain in the body is always constant, which is called Young’s modulus of elasticity. It is denoted by letter “Y” or “E”. Young’s modulus of elasticity is not defined for liquids and gases. The international standard symbols for Young’s modulus E is derived from word élasticité (French for elasticity), while some authors use Y as it is the first letter of the expression Young’s modulus of elasticity.
Its S.I. unit of stress is N m-2 (newton per square meter) or Pa (pascal) and its dimensions are [L-1M1T-2]. Mathematically,
Youn’s modulus of elasticity = Longitudinal stress / Longitudinal strain
Young’s Modulus of Elasticity of the Material of a Wire:
Consider a wire of length ‘L’ and radius of cross-section ‘r’ is fixed at one end and stretched by suspending a load of ‘mg’ from the other end. Let ‘l‘ be the extension produced in the wire when it is fully stretched.
Now, by the definition of Yong’s modulus of elasticity we have This is an expression for Young’s modulus of elasticity of a material of a wire.
This is an expression for Young’s modulus of elasticity of a material of a wire.
Characteristics of Young’s Modulus of Elasticity:
- Within the elastic limit, it is the ratio of longitudinal stress to longitudinal strain
- It is associated with the change in the length of a body.
- It exists in solid material bodies
- It is a measure of the stiffness of a solid material.
- Young’s modulus of the material of a wire is given by
Poisson’s Ratio:
The concept of this constant was introduced by physicist Simeon Poisson. When a rod or wire is subjected to tensile stress, its length increases in the direction of stress, but its transverse (lateral) dimensions decrease and vice-versa. i.e. when the length increase, the thickness decreases and vice-versa. In other words, we can say that the longitudinal strain is always accompanied by a transverse (lateral) strain.
The ratio of transverse strain to the corresponding longitudinal strain is called Poisson’s ratio. It is denoted by letter ‘m’. It has no unit. It is a dimensionless quantity.
Poisson’s Ratio = Lateral strain / Longitudinal strain
For homogeneous isotropic medium -1 ≤ m ≤ 0.5. In actual practice, Poisson’s ratio is always positive. There are some materials with a negative Poisson’s ratio. Poisson’s ratio of cork is zero, that of metal is 0.3 and that of rubber is 0.5.
Materials with a negative value of Poisson’s ratio are said to be auxetic. They grow larger in the transverse direction when stretched and smaller when compressed. Most auxetic materials are polymers with a crumpled, foamy structure. Pulling the foam causes the crumples to unfold and the whole network expands in the transverse direction.
Previous Topic: Concept of Elasticity, Plasticity, and Rigidity
Next Topic: Numerical Problems on Stress, Strain, and Young’s Modulus of Elasticity